



Next: Bons Antecedentes Algébricos
Up: Tópicos de matemática quântica
Previous: Referências
1. Aqui se pretende expor os elementos
de grupos quânticos de
forma simples e direta.
As construções não serão
apresentadas da maneira mais geral
possível, e serão sempre
acompanhadas no exemplo
(já extremamente interessante) do grupo quântico
``mais simples'' Slq(2), deformação
do grupo algébrico semisimples Sl(2). Um contexto
definitivamente algébrico será adotado:
por exemplo,
evitaremos menções a álgebras C*, e outros
objetos analíticos. A virtude maior desta
filosofia é destacar claramente
a natureza (co- ou contra- variante)
das operações
envolvidas, dos diversos tipos de produtos,
de cada conceito.
2.
Não há definição satisfatória
universalmente reconhecida do que seja um grupo
quântico. Todas as propostas
em vigor sugerem a idéia
de deformação de um objeto clássico,
que pode ser,
por exemplo, um grupo algébrico, ou um grupo
de Lie. E em todas as propostas os objetos deformados
perdem as propriedades de grupo: assim,
``grupos" quânticos não são grupos. O que sempre
se procura preservar nas deformações é
o entendimento das diversas representações
que os objetos admitem.
3.
Fixemos as idéias postulando
uma dualidade básica que a
Matemática deste século refletiu
em uma quantidade de linguagens
diferentes: por um lado, são estudados
objetos X que possuem uma estrutura geométrica
ou topológica. A tais objetos são associadas
construções algébricas A(X), que podem
ser, por exemplo, álgebras de funções
definidas no conjunto X, ou o espaço
de seções de um fibrado vetorial.
Frequentemente gostaríamos de reler
nestas álgebras as estruturas geométricas
originais, isto é, gostaríamos de recuperar
em A(X) nossos objetos iniciais X através
de alguma noção de espectro S(A(X))
da álgebra A(X):
a situação mais desejada é quando
voltamos a ter alguma forma de isomorfismo
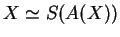 .
O retorno à Geometria a partir das
álgebras A(X) através
de um espectro sugere considerarmos espectros
S(A) de álgebras mais gerais A. Tais
espectros são
objetos que possuem ainda uma Geometria reminescente,
quase sempre muito interessante.
4.
Esta separação básica,
por um lado a Álgebra
em A, e por outro a Geometria (ou Topologia)
em X ou em S(A), é uma situação
ideal: os objetos que vemos na realidade
matemática nos chegam frequentemente
misturados. São,
por exemplo, grupos topológicos,
ou espaços vetoriais topológicos, objetos
que tem simultaneamente estruturas algébricas
e geométricas de alguma forma
compatíveis. A aplicação
dos funtores usuais A de algebrização
em um objeto X assim
fornece estruturas algébricas adicionais
sobre os objetos já algébricos A(X), que
passam então a admitir, por dualidade,
co-multiplicações.
5.
Como um exemplo-paradigma tomamos
um grupo algébrico linear X: algebricamente,
um grupo, geometricamente uma variedade...
algébrica (a notação consagrada não
pode evitar armadilhas); além disso, as
operações de grupo são morfismos
de variedades algébricas. O exemplo
que nos será mais caro é o
grupo algébrico Sl2(k). Como para toda
variedade algébrica, podemos considerar
um funtor de algebrização que associa
a cada variedade X seu anel de funções
regulares R(X). A estrutura adicional de
grupo em X doa, por dualidade à la Yoneda,
uma estrutura de co-algebra em R(X)
(definições precisas mais tarde).
Como segundo exemplo-paradigma tomemos
X um grupo de Lie, isto é: geometricamente
uma variedade, algebricamente um grupo, com
a compatibilidade fundamental de
serem diferenciáveis as operações
algébricas. Também aqui se manifesta
o ubíquo Sl2. Um funtor
de algebrização básico para uma variedade
é a consideração de seu fibrado tangente;
no caso do grupo de Lie X, este funtor fornece
a álgebra de Lie
.
O retorno à Geometria a partir das
álgebras A(X) através
de um espectro sugere considerarmos espectros
S(A) de álgebras mais gerais A. Tais
espectros são
objetos que possuem ainda uma Geometria reminescente,
quase sempre muito interessante.
4.
Esta separação básica,
por um lado a Álgebra
em A, e por outro a Geometria (ou Topologia)
em X ou em S(A), é uma situação
ideal: os objetos que vemos na realidade
matemática nos chegam frequentemente
misturados. São,
por exemplo, grupos topológicos,
ou espaços vetoriais topológicos, objetos
que tem simultaneamente estruturas algébricas
e geométricas de alguma forma
compatíveis. A aplicação
dos funtores usuais A de algebrização
em um objeto X assim
fornece estruturas algébricas adicionais
sobre os objetos já algébricos A(X), que
passam então a admitir, por dualidade,
co-multiplicações.
5.
Como um exemplo-paradigma tomamos
um grupo algébrico linear X: algebricamente,
um grupo, geometricamente uma variedade...
algébrica (a notação consagrada não
pode evitar armadilhas); além disso, as
operações de grupo são morfismos
de variedades algébricas. O exemplo
que nos será mais caro é o
grupo algébrico Sl2(k). Como para toda
variedade algébrica, podemos considerar
um funtor de algebrização que associa
a cada variedade X seu anel de funções
regulares R(X). A estrutura adicional de
grupo em X doa, por dualidade à la Yoneda,
uma estrutura de co-algebra em R(X)
(definições precisas mais tarde).
Como segundo exemplo-paradigma tomemos
X um grupo de Lie, isto é: geometricamente
uma variedade, algebricamente um grupo, com
a compatibilidade fundamental de
serem diferenciáveis as operações
algébricas. Também aqui se manifesta
o ubíquo Sl2. Um funtor
de algebrização básico para uma variedade
é a consideração de seu fibrado tangente;
no caso do grupo de Lie X, este funtor fornece
a álgebra de Lie
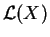 ,
o espaço
tangente na identidade. Um funtor intra-algébrico
agora asocia a cada álgebra de Lie
,
o espaço
tangente na identidade. Um funtor intra-algébrico
agora asocia a cada álgebra de Lie 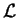 a álgebra (associativa)
envolvente
a álgebra (associativa)
envolvente
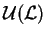 de forma
universal (este funtor, que deve ser chamado de
funtor de Poincaré-Birkhoff-Witt, é o
adjunto à esquerda do funtor que a cada álgebra
associativa A associa a álgebra de Lie
com o colchete dado da forma ``usual'':
[a,b]=ab-ba).
Estes exemplos serão nossos guias.
6.
Se o objeto inicial X for um objeto assim misto,
dotado de estruturas algébricas e geométricas
simultaneamente, as deformações que procuramos
operam nas álgebras A(X),
enriquecidas por co-multiplicações, para gerar
objetos Aq(X) da mesma natureza
igualmente enriquecida.
O parâmetro q de deformação intervem
nas definições das álgebras A(X)
(ou mais simplesmente A) de uma forma
que a primeira vista
pode parecer arbitrária: confiamos
então na relevância destas definições
distorcidas que uma quantidade de aplicações
físicas, muitas vezes não relacionadas
entre si, indica.
Poderíamos pensar em aplicar espectros e obter
alguma Geometria em
de forma
universal (este funtor, que deve ser chamado de
funtor de Poincaré-Birkhoff-Witt, é o
adjunto à esquerda do funtor que a cada álgebra
associativa A associa a álgebra de Lie
com o colchete dado da forma ``usual'':
[a,b]=ab-ba).
Estes exemplos serão nossos guias.
6.
Se o objeto inicial X for um objeto assim misto,
dotado de estruturas algébricas e geométricas
simultaneamente, as deformações que procuramos
operam nas álgebras A(X),
enriquecidas por co-multiplicações, para gerar
objetos Aq(X) da mesma natureza
igualmente enriquecida.
O parâmetro q de deformação intervem
nas definições das álgebras A(X)
(ou mais simplesmente A) de uma forma
que a primeira vista
pode parecer arbitrária: confiamos
então na relevância destas definições
distorcidas que uma quantidade de aplicações
físicas, muitas vezes não relacionadas
entre si, indica.
Poderíamos pensar em aplicar espectros e obter
alguma Geometria em
S(Aq(X)), mas a ênfase
maior das aplicações tem sido em recuperar
a teoria de representações de X, que
em geral é equivalente à de A(X), para
as álgebras deformadas Aq(X).
7. (Sobre estas notas)
O conceito de grupos
quânticos foi motivado por problemas vindos
de um grande número de situações físicas,
e com isso o entendimento das idéias que motivaram
a teoria requer naturalmente um amplo conhecimento
anterior. No entanto, o trabalho de manipulação
da teoria pode ser efetuado em um nível muito
mais modesto; estas notas procuram contemplar
situações de pré-requisitos bastante diversas.
Idealmente, qualquer leitor com algum interesse
poderia achar nelas um lugar de trabalho matemático
ativo. Alguma informação categórica está
recolhida em apêndice: a mistura de estruturas
que os grupos quânticos exemplificam torna
a linguagem categórica um dado essencial.
Índice do Capítulo 5
I. Bons Antecedentes Algébricos
I.1 Grupos Clássicos: Definições
I.2 A Geometria dos Grupos Clássicos
I.3 A Álgebra dos Grupos Clássicos
I.4 Álgebras de Lie e Álgebras Envolventes
I.5 Representações
II. Grupos Quânticos
II.1 O Plano Quântico, as Matrizes
Quânticas e os Grupos Quânticos
II.2 A Álgebra Envolvente
II.3 Módulos




Next: Bons Antecedentes Algébricos
Up: Tópicos de matemática quântica
Previous: Referências
Nicolau C. Saldanha
1999-08-10