A primeira seção deste trabalho terminou num impasse: disputando prioridade sobre o estudo dos grupos clássicos, os algebristas chamaram à atenção que estes grupos eram funtores
A primeira seção deste trabalho terminou
num impasse: disputando prioridade sobre o estudo
dos grupos clássicos, os algebristas chamaram
à atenção que estes grupos eram funtores
![]() (uma
terminologia francesa original era funtores
em grupos; depois foi acatada a
denominação esquemas afins de grupo).
Estes funtores eram representáveis, e tudo a ser
feito com eles podia ser feito, conforme Yoneda
dizia, com os objetos que os representavam. Ora,
estes objetos eram álgebras de Hopf
comutativas sobre k, e a categoria
(uma
terminologia francesa original era funtores
em grupos; depois foi acatada a
denominação esquemas afins de grupo).
Estes funtores eram representáveis, e tudo a ser
feito com eles podia ser feito, conforme Yoneda
dizia, com os objetos que os representavam. Ora,
estes objetos eram álgebras de Hopf
comutativas sobre k, e a categoria
![]() ganhou fama e fortuna entre
os algebristas.
ganhou fama e fortuna entre
os algebristas.
Os geômetras, por outro lado, viam os grupos
clássicos como grupos de Lie, eram levados a
estudar suas álgebras de Lie correspondentes e,
para fugir da não associatividade, passavam às
álgebras envolventes, tendo aplicado o funtor
composto
![]() .
Ora, as álgebras onde caíram
eram naturalmente álgebras de Hopf sobre k
não comutativas, mas co-comutativas.
.
Ora, as álgebras onde caíram
eram naturalmente álgebras de Hopf sobre k
não comutativas, mas co-comutativas.
Salomonicamente, a teoria de grupos quânticos
postula que a categoria a estudar é
![]() ,
a categoria das álgebras
de Hopf não (necessariamente) comutativas
nem co-comutativas. A motivação veio do
fato de os físicos terem que trabalhar
com relações de comutação exóticas,
o que os levaram a postular o plano
quântico, a ser definido a seguir.
,
a categoria das álgebras
de Hopf não (necessariamente) comutativas
nem co-comutativas. A motivação veio do
fato de os físicos terem que trabalhar
com relações de comutação exóticas,
o que os levaram a postular o plano
quântico, a ser definido a seguir.
O plano comum A2, para
A uma álgebra comutativa
sobre k, pode ser visto como o funtor
representável
![]() representado pela álgebra de polinômios
em duas variáveis comutativas
k[X1,X2]: a cada
par ordenado (a,b) é associado o único
morfismo em
representado pela álgebra de polinômios
em duas variáveis comutativas
k[X1,X2]: a cada
par ordenado (a,b) é associado o único
morfismo em
![]() satisfazendo
satisfazendo
![]() .
Incidentalmente, o grupo abeliano subjacente
a A2 torna k[x,y] co-objeto de Hopf em
.
Incidentalmente, o grupo abeliano subjacente
a A2 torna k[x,y] co-objeto de Hopf em
![]() ,
ou seja, uma álgebra de Hopf
comutativa, com a co-multiplicação dada por
,
ou seja, uma álgebra de Hopf
comutativa, com a co-multiplicação dada por
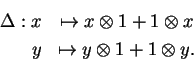
O golpe
de estado que os físicos tramaram foi considerar
o plano quântico baseado no anel de polinômios
em duas variáveis não-comutativas,
denotado por ![]() ,
e nele tomar o
ideal bilateral Iq gerado pelo elemento
,
e nele tomar o
ideal bilateral Iq gerado pelo elemento
| yx-qxy, | (II.1.1) |
A terminologia adotada confunde o plano quântico
com a álgebra que o representa. Para uma álgebra
A, objeto de
![]() ,
elementos
do conjunto
,
elementos
do conjunto
A álgebra kq[x,y] é noetheriana, naturalmente
graduada, não tem divisores de zero e tem o
conjunto de monômios
No que se segue é assumido
![]() .
.
Na situação clássica
o conjunto das matrizes
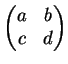 com coeficientes em uma
álgebra comutativa A é identificado com
com coeficientes em uma
álgebra comutativa A é identificado com
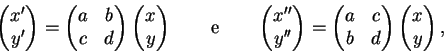
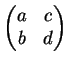 à esquerda e à
direita, as relações
y'x'=qx'y' e
y''x''=qx''y'' são equivalentes às
relações
à esquerda e à
direita, as relações
y'x'=qx'y' e
y''x''=qx''y'' são equivalentes às
relações
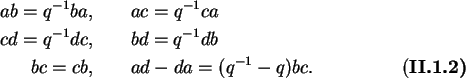
Com isso, o conjunto das matrizes que vão
operar no plano quântico kq[x,y]
são definidas por
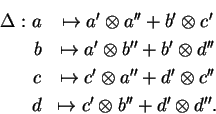
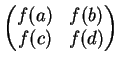 para o ponto f é inevitável.
para o ponto f é inevitável.
As matrizes ![]() e o plano
estão assim definidos, bem como o(s) produto(s)
de uma matriz por um vetor. A próxima
definição é
e o plano
estão assim definidos, bem como o(s) produto(s)
de uma matriz por um vetor. A próxima
definição é
| (II.1.3) |
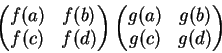
Em
![]() é definida uma
co-multiplicação
é definida uma
co-multiplicação ![]() e uma co-unidade
e uma co-unidade ![]() que generalizam o caso comutativo:
que generalizam o caso comutativo:
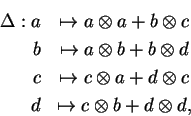
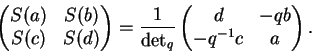
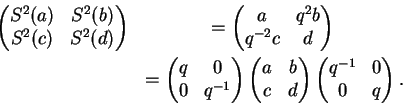
Exemplos e Exercícios
1. Seja B a álgebra comutativa
Considere
a álgebra não comutativa A,
subálgebra de
![]() ,
gerada por
,
gerada por ![]() e
e ![]() ,
onde
,
onde
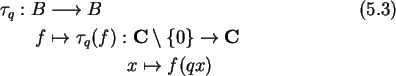
e
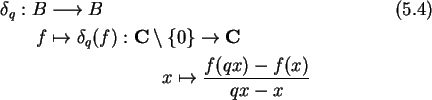
O par
![]() é um ponto de
kq[x,y] definido sobre A. Quando q tende
a 1,
é um ponto de
kq[x,y] definido sobre A. Quando q tende
a 1, ![]() tende para a derivada usual.
tende para a derivada usual.