



Next: Módulos
Up: Grupos Quânticos
Previous: O Plano Quântico, as
No que se segue 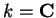 será
uma hipótese
simplificadora (sem ser trivializante).
será
uma hipótese
simplificadora (sem ser trivializante).
Definimos a álgebra
 como sendo a álgebra (associativa)
gerada pelos símbolos
E,F,K,K-1
e L submetidos às relações
como sendo a álgebra (associativa)
gerada pelos símbolos
E,F,K,K-1
e L submetidos às relações
e
Se 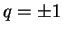 então K2=1, e K
comuta então com os demais geradores,
estando assim no centro
então K2=1, e K
comuta então com os demais geradores,
estando assim no centro
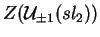 .
Se q=1
então fazendo
X=EK, Y=F e H=LK valem as
relações
.
Se q=1
então fazendo
X=EK, Y=F e H=LK valem as
relações
[X,Y]=[EK,F]=[E,F]K=LK=H,
[H,Y]=[LK,EK]=[L,E]=2EK=2X
e
[H,Y]=[LK,F]=[L,F]K=-2FK2=-2Y.
Cotejando estas relações com as
relações de definição
de
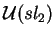 (listadas em
1. de (I.4)), fica claro
que existe em epimorfismo
em
(listadas em
1. de (I.4)), fica claro
que existe em epimorfismo
em
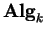
satisfazendo
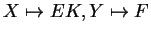 e
e
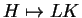 ,
e de fato vale
,
e de fato vale
e a álgebra
 pode
assim ser vista como uma deformação
da álgebra envolvente
pode
assim ser vista como uma deformação
da álgebra envolvente
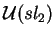 ,
como a notação sugere.
,
como a notação sugere.
A álgebra envolvente quântica
 assim definida pode
ser apresentada, se
assim definida pode
ser apresentada, se
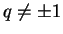 ,
de uma forma mais simples
como sendo a álgebra (associativa)
gerada pelos símbolos E,F,K e
K-1
submetidos às relações
,
de uma forma mais simples
como sendo a álgebra (associativa)
gerada pelos símbolos E,F,K e
K-1
submetidos às relações
como acima,
e
O isomorfismo entre estas duas
apresentações identifica letras
que combinam, o único ponto
não trivial é mostrar que as
relações ``mais complexas''
envolvendo L,
da primeira apresentação,
são satisfeitas, mas isto é
uma fácil manipulação.
Supondo
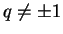 ,
será
usada preferencialmente a segunda
apresentação de
,
será
usada preferencialmente a segunda
apresentação de
 ,
por ser mais simples.
,
por ser mais simples.
Assim,
 é noetheriana, sem divisores de zero, e
tem como base
é noetheriana, sem divisores de zero, e
tem como base
além disso,
 admite um automorfismo
admite um automorfismo
satisfazendo
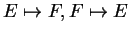 e
e
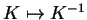 ,
e um antiautomorfismo
,
e um antiautomorfismo
satisfazendo
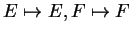 e
e
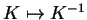 .
(Dada uma álgebra A
sobre k, objeto de
.
(Dada uma álgebra A
sobre k, objeto de
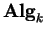 ,
a
álgebra oposta Aop tem o mesmo
espaço vetorial subjacente e a
multiplicação oposta: o produto
ab em Aop é o produto ba em
A. Esta definição é uma dádiva
do fato de os axiomas de anel serem auto-duais;
se A é comutativa então A=Aop).
,
a
álgebra oposta Aop tem o mesmo
espaço vetorial subjacente e a
multiplicação oposta: o produto
ab em Aop é o produto ba em
A. Esta definição é uma dádiva
do fato de os axiomas de anel serem auto-duais;
se A é comutativa então A=Aop).
Dotando os geradores dos graus gr(E)=1,
gr(F)-1 e
gr(K)=gr(K-1)=0, as
relações que definem
 são homogêneas, e logo
são homogêneas, e logo
 admite uma gradação natural em que
o monômio EIFjKl tem grau i-j.
Se
admite uma gradação natural em que
o monômio EIFjKl tem grau i-j.
Se
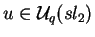 tem grau g
então se deduz das relações de
definição que
tem grau g
então se deduz das relações de
definição que
KuK-1=q2gu.
Se q nao for raiz da unidade estes
autovalores qg são distintos, e a
parte homogênea de grau g de
 são os autoespaços
de
são os autoespaços
de
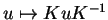 .
Se q for raiz
da unidade a graduação de
.
Se q for raiz
da unidade a graduação de
 refina esta decomposição
em autoespaços.
refina esta decomposição
em autoespaços.
A subálgebra
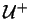 (resp.,
(resp.,
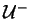 )
de
)
de
 gerada por E (resp.,
por F) tem como base
gerada por E (resp.,
por F) tem como base
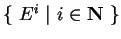 (resp.,
(resp.,
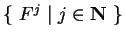 ). Assim,
). Assim,
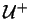 e
e
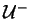 são comutativas, isomorfas a k[T].
são comutativas, isomorfas a k[T].
A subálgebra
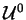 de
de
 gerada por K e K-1
tem como base
gerada por K e K-1
tem como base
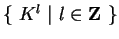 .
Assim,
.
Assim,
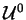 é comutativa, isomorfa à localização
k[T,T-1] de k[T].
é comutativa, isomorfa à localização
k[T,T-1] de k[T].
A álgebra envolvente quântica tem
 admite um elemento
de Casimir quântico Cq dado
por
admite um elemento
de Casimir quântico Cq dado
por
Este elemento Cq está no centro
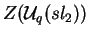 de
de
 e satisfaz
e satisfaz
A álgebra envolvente quântica tem
 uma
estrutura de álgebra de Hopf, como se esperaria
por ser deformação de
uma
estrutura de álgebra de Hopf, como se esperaria
por ser deformação de
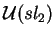 ,
dada pela
comultiplicação
,
dada pela
comultiplicação
a co-unidade
e o antípoda
Novamente
 não é nem comutativa
nem co-comutativa, como se vê do fato de o
antípoda não ser involutivo.
não é nem comutativa
nem co-comutativa, como se vê do fato de o
antípoda não ser involutivo.




Next: Módulos
Up: Grupos Quânticos
Previous: O Plano Quântico, as
Nicolau C. Saldanha
1999-08-10
![]() como sendo a álgebra (associativa)
gerada pelos símbolos
E,F,K,K-1
e L submetidos às relações
como sendo a álgebra (associativa)
gerada pelos símbolos
E,F,K,K-1
e L submetidos às relações
![]() assim definida pode
ser apresentada, se
assim definida pode
ser apresentada, se
![]() ,
de uma forma mais simples
como sendo a álgebra (associativa)
gerada pelos símbolos E,F,K e
K-1
submetidos às relações
,
de uma forma mais simples
como sendo a álgebra (associativa)
gerada pelos símbolos E,F,K e
K-1
submetidos às relações
![\begin{displaymath}[E,F]=\frac{K-K^{-1}}{q-q^{-1}}.\end{displaymath}](img1207.gif)
![]() é noetheriana, sem divisores de zero, e
tem como base
é noetheriana, sem divisores de zero, e
tem como base
![]() são homogêneas, e logo
são homogêneas, e logo
![]() admite uma gradação natural em que
o monômio EIFjKl tem grau i-j.
Se
admite uma gradação natural em que
o monômio EIFjKl tem grau i-j.
Se
![]() tem grau g
então se deduz das relações de
definição que
tem grau g
então se deduz das relações de
definição que
![]() (resp.,
(resp.,
![]() )
de
)
de
![]() gerada por E (resp.,
por F) tem como base
gerada por E (resp.,
por F) tem como base
![]() (resp.,
(resp.,
![]() ). Assim,
). Assim,
![]() e
e
![]() são comutativas, isomorfas a k[T].
são comutativas, isomorfas a k[T].
![]() de
de
![]() gerada por K e K-1
tem como base
gerada por K e K-1
tem como base
![]() .
Assim,
.
Assim,
![]() é comutativa, isomorfa à localização
k[T,T-1] de k[T].
é comutativa, isomorfa à localização
k[T,T-1] de k[T].
![]() admite um elemento
de Casimir quântico Cq dado
por
admite um elemento
de Casimir quântico Cq dado
por
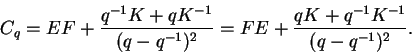
![]() uma
estrutura de álgebra de Hopf, como se esperaria
por ser deformação de
uma
estrutura de álgebra de Hopf, como se esperaria
por ser deformação de
![]() ,
dada pela
comultiplicação
,
dada pela
comultiplicação