B.1. Variedades. A Análise que será utilizada aqui é real e euclidiana, baseada nos espaços
Este apêndice resume
brevemente os fatos necessários
da categoria diferenciável, e assume do
leitor alguma lembrança de Análise.
Especificamente, esta categoria é definida
para agregar todo conhecimento local
da Análise. Assim não haverá necessidade
de se lembrar de nenhuma fórmula de
Cálculo, mas sim dos teoremas locais
de existência:
o teorema da função inversa e o teorema
da função implícita.
B.1. Variedades.
A Análise que será utilizada aqui é real e
euclidiana, baseada nos espaços ![]() .
Apesar disso, seguindo os passos dos mestres
em [M-S],
adotamos a idéia de introduzir
um espaço ambiente
do tipo
.
Apesar disso, seguindo os passos dos mestres
em [M-S],
adotamos a idéia de introduzir
um espaço ambiente
do tipo ![]() onde A
é um conjunto qualquer, objeto de Conj.
Este espaço ambiente nada mais é do que
onde A
é um conjunto qualquer, objeto de Conj.
Este espaço ambiente nada mais é do que
Cada elemento ![]() é uma coordenada em
é uma coordenada em
![]() ,
definindo
uma função de projeção
,
definindo
uma função de projeção
Os objetos da categoria diferenciável
Diff
serão subconjuntos M em
Além de espaço topológico,
uma estrutura adicional que Y tiver
permite considerar a função
![]() como morfismo em outras categorias.
O exemplo relevante é
o de um subconjunto de um espaço
euclidiano no qual é possível
tomar derivadas: se
como morfismo em outras categorias.
O exemplo relevante é
o de um subconjunto de um espaço
euclidiano no qual é possível
tomar derivadas: se
![]() então uma função
então uma função
![]() é suave se para cada
é suave se para cada
![]() as compostas
as compostas
![]() forem
infinitamente diferenciáveis.
As derivadas parciais
forem
infinitamente diferenciáveis.
As derivadas parciais
![]() são definidas
como as funções
são definidas
como as funções
Estas simples considerações
permitem a postulação da categoria
Diff: um subconjunto
![]() é uma variedade diferenciável
de dimensão n se para cada
é uma variedade diferenciável
de dimensão n se para cada
![]() existir
uma função suave
existir
uma função suave
![]() ,
definida em um aberto
,
definida em um aberto
![]() ,
tal que
h seja um homeomorfismo de U em
,
tal que
h seja um homeomorfismo de U em
![]() e que para
e que para ![]() com h(u)=x
a matrix
com h(u)=x
a matrix
![]() tenha posto n. Neste caso é dito
que V=h(U) é uma vizinhança
coordenada e (U,V,h) uma
parametrização local.
tenha posto n. Neste caso é dito
que V=h(U) é uma vizinhança
coordenada e (U,V,h) uma
parametrização local.
Casos simples mas importantes de
variedades são os próprios
abertos U em ![]() ,
para
qualquer ponto dos quais é possível
tomar a mesma
parametrização
,
para
qualquer ponto dos quais é possível
tomar a mesma
parametrização
![]() .
Em particular o
espaço euclidiano
.
Em particular o
espaço euclidiano ![]() é
uma variedade diferenciável
de dimensão n.
é
uma variedade diferenciável
de dimensão n.
B.2. Mudança de parametrização.
Segue do teorema da função
implícita que se duas
parametrizações locais
(U,V,h) e
(U',V',h') se encontram,
isto é, são tais que
![]() então
então
B.3. Funções suaves.
Parametrizações locais são
usadas na definição dos morfismos
na categoria Diff de variedades
diferenciáveis.
Estes morfismos, ditos funções
suaves, são definidos a partir do
conceito de funções suaves
definidas em um aberto
![]() como em B.1:
sejam dadas duas variedades
como em B.1:
sejam dadas duas variedades
![]() e
e
![]() ;
uma função
;
uma função
![]() é suave em um ponto
é suave em um ponto
![]() se para uma
parametrização local (U,V,h)
em M tal que
se para uma
parametrização local (U,V,h)
em M tal que ![]() tenhamos
tenhamos
![]() suave. O resultado enunciado em
B.2
implica que esta a definição
de suavidade em um ponto
suave. O resultado enunciado em
B.2
implica que esta a definição
de suavidade em um ponto ![]() independe da escolha da
parametrização local (U,V,h)
com
independe da escolha da
parametrização local (U,V,h)
com ![]() .
Uma função
.
Uma função
![]() é suave
se for suave em cada ponto
é suave
se for suave em cada ponto ![]() .
Variedades diferenciáveis e
funções suaves entre elas
definem a categoria Diff.
Isomorfismos em Diff são
chamados difeomorfismos.
.
Variedades diferenciáveis e
funções suaves entre elas
definem a categoria Diff.
Isomorfismos em Diff são
chamados difeomorfismos.
Para um aberto
![]() tomado com a estrutura natural de
variedade como em B.1 o conceito
de função suave como morfismo
em
tomado com a estrutura natural de
variedade como em B.1 o conceito
de função suave como morfismo
em
![]() coincide
com a noção introduzida em B.1.
coincide
com a noção introduzida em B.1.
Pela própria postulação dos objetos como conjuntos com uma estrutura adicional (que permite tomar derivadas), há funtores de esquecimento de Diff para Conj e para Top, mas estes funtores são pouco interessantes: a estrutura adicional de variedade é excessivamente ligada aos processos da Análise para que estes funtores tenham algum adjunto. No entanto, Diff possui produtos construídos sobre o produto cartesiano.
B.4. Sobre a definição de
variedades.
A definição de variedade pode
ser apresentada de muitas maneiras
diferentes. O tratamento adotado
aqui é calcado em [M-S] e
sofre o defeito de exigir que a
variedade
![]() esteja definida em um
espaço ambiente
esteja definida em um
espaço ambiente
![]() ,
que depende do conjunto A
que aparentemente pouco se manifesta
na estrutura diferencial. Esta
dependência, de fato, é
algo irrelevante:
se
,
que depende do conjunto A
que aparentemente pouco se manifesta
na estrutura diferencial. Esta
dependência, de fato, é
algo irrelevante:
se
![]() é monomorfismo
em Conj então
é monomorfismo
em Conj então
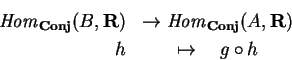
Há, no entanto, um conjunto A
máximo ``canônico'': dada uma variedade
![]() ,
para cada
,
para cada ![]() temos a função
temos a função
![]() que é suave, isto é, um morfismo
em
que é suave, isto é, um morfismo
em
![]() ,
e a identificação
,
e a identificação
![]() injeta A como subconjunto de
injeta A como subconjunto de
![]() .
Tomemos então
.
Tomemos então
Agora a variedade
![]() é apresentada de forma
intrínseca, e este processo
pode ser usado para uma redefinição:
dado um conjunto M em Conj
e
é apresentada de forma
intrínseca, e este processo
pode ser usado para uma redefinição:
dado um conjunto M em Conj
e
![]() um
subconjunto de funções
reais em M que
separa pontos, isto é,
tal que a aplicação canônica
um
subconjunto de funções
reais em M que
separa pontos, isto é,
tal que a aplicação canônica
![]() definida
como acima seja uma injeção
(esta condição esmiuçada
significa: dados
definida
como acima seja uma injeção
(esta condição esmiuçada
significa: dados
![]() existe
existe ![]() com
com
![]() ), A é chamado uma
estrutura diferencial em M
se
), A é chamado uma
estrutura diferencial em M
se
![]() for uma variedade diferenciável
e se
for uma variedade diferenciável
e se
![]() ,
isto é,
se A for o conjunto de morfismos
em Diff (isto é,
de funções suaves)
desta variedade para a reta R.
,
isto é,
se A for o conjunto de morfismos
em Diff (isto é,
de funções suaves)
desta variedade para a reta R.
B.5. O espaço tangente.
Seja
![]() uma variedade de dimensão n
e
uma variedade de dimensão n
e ![]() .
Um
caminho passando por m
é uma função
suave
.
Um
caminho passando por m
é uma função
suave
Se (U,V,h) for uma parametrização
local com
![]() ,
digamos
m=h(x) para
,
digamos
m=h(x) para
![]() ,
então
,
então
![]() é vetor tangente em m se e só
se existir uma combinação linear
é vetor tangente em m se e só
se existir uma combinação linear
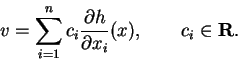
O fibrado tangente de M
é o subconjunto
![]() dado por
dado por
A associação
![]() é (a função nos objetos
de) um funtor
é (a função nos objetos
de) um funtor
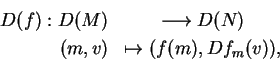
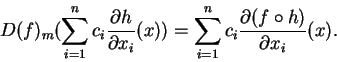
Por exemplo, para toda variedade
M a associação
![]() define uma função suave
define uma função suave
![]() .
A derivada
.
A derivada
![]() é calculada associando
ao vetor velocidade do caminho
é calculada associando
ao vetor velocidade do caminho
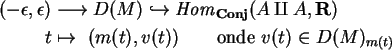
o vetor velocidade
![]() ,
isto é,
,
isto é,
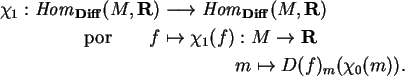
A associação
![]()
identifica o espaço de campos vetoriais
com a álgebra de derivações
de
![]() ,
e assim
Vect(M) ganha uma estrutura de álgebra
de Lie.
,
e assim
Vect(M) ganha uma estrutura de álgebra
de Lie.