A.1 Categorias, funtores e transformações
naturais.
Uma categoria C é uma classe de objetos
tal que:
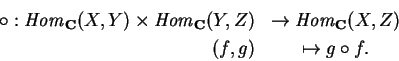
Estes dados estão sujeitos aos seguintes axiomas:
Dados dois funtores ![]() e
e
![]() entre as categorias C
e D uma transformação
natural
entre as categorias C
e D uma transformação
natural ![]() entre
entre
![]() e
e ![]() ,
denotada
,
denotada
![]() ,
é a especificação, para cada objeto
X de C, de um elemento
,
é a especificação, para cada objeto
X de C, de um elemento
![]() .
Este dado é sujeito
ao seguinte axioma
.
Este dado é sujeito
ao seguinte axioma
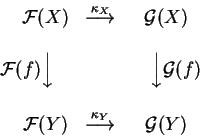
Categorias, funtores e transformações
naturais formam
o contexto natural de trabalho do que
faremos a seguir.
Os objetos comumente estudados em álgebra e Topologia
naturalmente se constituem em categorias:
por exemplo, a
categoria dos grupos, denotada por
Grp, tem por objetos
grupos e por morfismos homomorfismos
de grupos, e analogamente para
a categoria dos aneis, denotada por An,
para a categoria dos
módulos à esquerda sobre um anel A,
denotada por
![]() ,
para a categoria Top que
tem por objetos espaços topológicos e
por morfismos funções
contínuas, e assim por diante. Os
objetos destas categorias são
conjuntos dotados de uma estrutura
adicional (de grupo, espaço
topológico, etc) e os morfismos
são as funções entre os objetos
que preservam esta estrutura
adicional. Estas categorias são
chamadas categorias concretas,
e se caracterizam pela existência de um funtor fiel
,
para a categoria Top que
tem por objetos espaços topológicos e
por morfismos funções
contínuas, e assim por diante. Os
objetos destas categorias são
conjuntos dotados de uma estrutura
adicional (de grupo, espaço
topológico, etc) e os morfismos
são as funções entre os objetos
que preservam esta estrutura
adicional. Estas categorias são
chamadas categorias concretas,
e se caracterizam pela existência de um funtor fiel
![]() ,
onde Conj
é a categoria que tem
por objetos, conjuntos, e por morfismos,
funções, e
,
onde Conj
é a categoria que tem
por objetos, conjuntos, e por morfismos,
funções, e ![]() é dito funtor de esquecimento,
que associa a cada objeto
de C o conjunto subjacente
sobre o qual é construida a
estrutura adicional. (Um funtor é
fiel se for injetor em
cada conjunto de morfismos e
é pleno se for sobrejetor
nestes conjuntos).
é dito funtor de esquecimento,
que associa a cada objeto
de C o conjunto subjacente
sobre o qual é construida a
estrutura adicional. (Um funtor é
fiel se for injetor em
cada conjunto de morfismos e
é pleno se for sobrejetor
nestes conjuntos).
Há também funtores de esquecimento como
![]() ,
que
esquece a estrutura multiplicativa
dos anéis,
,
que
esquece a estrutura multiplicativa
dos anéis,
![]() ,
e assim por diante.
,
e assim por diante.
Dadas duas transformações naturais
![]() e
e
![]() de funtores
de funtores
![]() e
e
![]() de C
em D,
podemos considerar as compostas
a nível de cada objeto
X de C:
de C
em D,
podemos considerar as compostas
a nível de cada objeto
X de C:
![]() .
Assim, as transformações naturais
entre funtores de C em D se compõem, e
esta composição obedece aos axiomas
(A.1.1) e (A.1.2), de maneira que
transformações naturais são
morfismos de uma categoria
denotada por
.
Assim, as transformações naturais
entre funtores de C em D se compõem, e
esta composição obedece aos axiomas
(A.1.1) e (A.1.2), de maneira que
transformações naturais são
morfismos de uma categoria
denotada por
![]() cujos objetos são
funtores de C em D.
cujos objetos são
funtores de C em D.
Dado um morfismo
![]() ,
se existir
,
se existir
![]() com
com
![]() (resp.,
(resp.,
![]() )
então g
é dito inversa à esquerda
(resp., inversa à direita) de f.
Se f tiver simultaneamente
inversa à esquerda e à direita
então f é dito
inversível, ou um isomorfismo.
Os morfismos de Conj que tem inversa à esquerda
são as funções injetoras,
os que tem inversas à direita são as
funções sobrejetoras e os
inversíveis são as funções bijetoras,
mas mesmo em categorias concretas,
tão próximas de Conj,
um morfismo pode ser dado por uma função injetora
sem que tenha uma inversa à esquerda: por exemplo,
a inclusão
)
então g
é dito inversa à esquerda
(resp., inversa à direita) de f.
Se f tiver simultaneamente
inversa à esquerda e à direita
então f é dito
inversível, ou um isomorfismo.
Os morfismos de Conj que tem inversa à esquerda
são as funções injetoras,
os que tem inversas à direita são as
funções sobrejetoras e os
inversíveis são as funções bijetoras,
mas mesmo em categorias concretas,
tão próximas de Conj,
um morfismo pode ser dado por uma função injetora
sem que tenha uma inversa à esquerda: por exemplo,
a inclusão
![]() em Anud,
a categoria dos anéis com unidade
(morfismos devem respeitar
esta condição e levar unidades em unidades).
Dois elementos
X e Y de C para os quais existe
em Anud,
a categoria dos anéis com unidade
(morfismos devem respeitar
esta condição e levar unidades em unidades).
Dois elementos
X e Y de C para os quais existe
![]() inversível são ditos
isomorfos. Assim, dois objetos
de Conj são isomorfos se e
só se tiverem a mesma
cardinalidade. Se C e D
são categorias e
inversível são ditos
isomorfos. Assim, dois objetos
de Conj são isomorfos se e
só se tiverem a mesma
cardinalidade. Se C e D
são categorias e
![]() e
e
![]() funtores satisfazendo
funtores satisfazendo
![]() e
e
![]() ,
isomorfismos naturais
em
,
isomorfismos naturais
em
![]() e
e
![]() ,
respectivamente,
então
,
respectivamente,
então
![]() ou
ou
![]() são chamados de
equivalências
de categorias. Uma equivalência
de categorias
são chamados de
equivalências
de categorias. Uma equivalência
de categorias
![]() como acima é necessariamente
um funtor pleno e fiel,
e além disso todo objeto de D
é isomorfo a um objeto da
forma
como acima é necessariamente
um funtor pleno e fiel,
e além disso todo objeto de D
é isomorfo a um objeto da
forma
![]() .
.
Dado um morfismo
![]() ,
se para
quaisquer
,
se para
quaisquer
![]() a equação
a equação
![]() implicar g=h então f é um
monomorfismo -- este será
certamente o caso se
f tiver uma inversa à esquerda. Dualmente, se para
quaisquer
implicar g=h então f é um
monomorfismo -- este será
certamente o caso se
f tiver uma inversa à esquerda. Dualmente, se para
quaisquer
![]() a
equação
a
equação
![]() implicar
g=h então f é um
epimorfismo -- este
será certamente o caso se
f tiver uma inversa à direita.
Em Conj todo monomorfismo
é uma injeção que
tem uma inversa à esquerda;
também, todo epimorfismo
é uma sobrejeção que
tem uma inversa à direita, mas
para ver isto é necessário
o uso do axioma da escolha.
Na categoria de anéis An
a inclusão
implicar
g=h então f é um
epimorfismo -- este
será certamente o caso se
f tiver uma inversa à direita.
Em Conj todo monomorfismo
é uma injeção que
tem uma inversa à esquerda;
também, todo epimorfismo
é uma sobrejeção que
tem uma inversa à direita, mas
para ver isto é necessário
o uso do axioma da escolha.
Na categoria de anéis An
a inclusão
![]() é um epimorfismo.
é um epimorfismo.
Dados dois monomorfismos
![]() e
e
![]() ,
dizemos que
,
dizemos que
![]() quando
existir
quando
existir
![]() ,
necessariamente um monomorfismo,
tal que
,
necessariamente um monomorfismo,
tal que
![]() .
Esta relação só não
é uma ordem parcial por falha da
anti-simetria, mas, como
é usual nestes casos, podemos passar
ao quociente pela relação de equivalência
que identifica
.
Esta relação só não
é uma ordem parcial por falha da
anti-simetria, mas, como
é usual nestes casos, podemos passar
ao quociente pela relação de equivalência
que identifica
![]() e
e
![]() para obter uma ordem
parcial no conjunto quociente,
denotado por
para obter uma ordem
parcial no conjunto quociente,
denotado por
![]() ;
um elemento deste conjunto
quociente é dito um subobjeto.
;
um elemento deste conjunto
quociente é dito um subobjeto.
A.2. O lema de Yoneda.
Um objeto X de uma categoria
C define naturalmente um funtor
covariante
![]() e um funtor contravariante
e um funtor contravariante
![]() de C para Conj da seguinte
maneira. A cada objeto Y de C o funtor
de C para Conj da seguinte
maneira. A cada objeto Y de C o funtor
![]() associa o conjunto
associa o conjunto
![]() e o funtor
e o funtor
![]() associa o conjunto
associa o conjunto
![]() ,
e a cada
morfismo
,
e a cada
morfismo
![]() o funtor
o funtor
![]() associa a função
associa a função
![]() obtida por
obtida por
![]() e o funtor
e o funtor
![]() associa a função
associa a função
![]() obtida
por
obtida
por
![]() .
Um
funtor
.
Um
funtor
![]() é representável
se for essencialmente obtido assim, isto é,
se existir um
objeto X em C e transformações
naturais
é representável
se for essencialmente obtido assim, isto é,
se existir um
objeto X em C e transformações
naturais
![]() e
e
![]() tais que para cada objeto
Y em C as composições
tais que para cada objeto
Y em C as composições
![]() e
e
![]() sejam identidades.
Dois funtores para os quais existe este par de
transformações
naturais são ditos naturalmente isomorfos.
Há uma definição
dual para um funtor contravariante representável.
sejam identidades.
Dois funtores para os quais existe este par de
transformações
naturais são ditos naturalmente isomorfos.
Há uma definição
dual para um funtor contravariante representável.
Dados um funtor
![]() e um objeto X em C,
uma transformação natural
e um objeto X em C,
uma transformação natural
![]() é inteiramente
descrita pela ação de
é inteiramente
descrita pela ação de ![]() em
em
![]() ;
com efeito,
para todo objeto Y em C temos que para
;
com efeito,
para todo objeto Y em C temos que para
![]() vale a igualdade
vale a igualdade
| (A.2.1) |
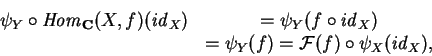
| (A.2.2) |
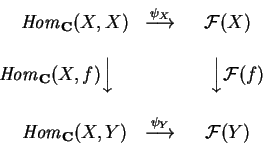
A.3. Limites.
Muitas construções comuns das categorias
usuais da álgebra
e da Topologia são exemplos do
conceito categórico de
limite, ou de colimite, seu dual: dados
uma categoria C,
uma categoria J (a ser usada
como índice) e um
funtor
![]() ,
um limite
de
,
um limite
de ![]() é um objeto
é um objeto
![]() em C
e, para cada objeto i de J, um morfismo
em C
e, para cada objeto i de J, um morfismo
![]() tal que para cada morfismo
tal que para cada morfismo
![]() temos
temos
![]() .
Estes dados devem obedecer
a uma propriedade dita universal:
para cada objeto X em C ao qual se associa
uma construção ``paralela'' à que
.
Estes dados devem obedecer
a uma propriedade dita universal:
para cada objeto X em C ao qual se associa
uma construção ``paralela'' à que
![]() possui, a saber,
para cada objeto i de J, temos um morfismo
possui, a saber,
para cada objeto i de J, temos um morfismo
![]() tal que para cada morfismo
tal que para cada morfismo
![]() tenhamos
tenhamos
![]() ,
deve existir um
único morfismo
,
deve existir um
único morfismo
![]() satisfazendo
satisfazendo
![]() para todo objeto i de J.
para todo objeto i de J.
Por exemplo, se J for
a categoria 2 que tem apenas dois objetos
1 e 2 e nenhum morfismo que
não seja a identidade, um funtor
![]() é simplesmente a
escolha de dois objetos
é simplesmente a
escolha de dois objetos
![]() para i=1,2 em
C, enquanto que um
limite
para i=1,2 em
C, enquanto que um
limite
![]() é um
objeto em C determinado por dois morfismos
é um
objeto em C determinado por dois morfismos
![]() para i=1,2, tal que para todo objeto
X de C dotado
de morfismos
para i=1,2, tal que para todo objeto
X de C dotado
de morfismos
![]() existe um
único morfismo
existe um
único morfismo
![]() para o qual
para o qual
![]() .
Este objeto
.
Este objeto
![]() é dito produto de X1 e X2, e
sempre existe se C
for uma das categorias Conj, Top
ou Grp, sendo simplesmente
o produto cartesiano de conjuntos,
o espaço topológico
produto ou o produto de grupos,
respectivamente.
é dito produto de X1 e X2, e
sempre existe se C
for uma das categorias Conj, Top
ou Grp, sendo simplesmente
o produto cartesiano de conjuntos,
o espaço topológico
produto ou o produto de grupos,
respectivamente.
Se Vaz for a categoria
sem objetos nem morfismos
então um funtor
![]() é vazio,
enquanto que um limite
é vazio,
enquanto que um limite
![]() é um
objeto em C
tal que para cada objeto
X de C existe um único
morfismo
é um
objeto em C
tal que para cada objeto
X de C existe um único
morfismo
![]() .
Este objeto
.
Este objeto
![]() é dito
objeto final em C, e
existe se C for
Conj (neste caso
é dito
objeto final em C, e
existe se C for
Conj (neste caso
![]() é qualquer
conjunto com um único elemento),
Top (
é qualquer
conjunto com um único elemento),
Top (
![]() será então o espaço
topológico construido sobre um
conjunto com um único
elemento com a única topologia possível)
ou Grp (
será então o espaço
topológico construido sobre um
conjunto com um único
elemento com a única topologia possível)
ou Grp (
![]() é o grupo trivial).
é o grupo trivial).
Se J for
a categoria Paral que tem apenas dois objetos
1 e 2 e cujos únicos
morfismos fora as identidades são descritos por
![]() ,
um funtor
,
um funtor
![]() é dado por
dois morfismos
é dado por
dois morfismos
![]() ,
enquanto que um limite
,
enquanto que um limite
![]() é um
objeto em C dado com um morfismo
é um
objeto em C dado com um morfismo
![]() satisfazendo
satisfazendo
![]() ,
tal que para todo objeto X de C dotado
de um morfismo
,
tal que para todo objeto X de C dotado
de um morfismo
![]() satisfazendo
satisfazendo
![]() existe um
único morfismo
existe um
único morfismo
![]() com
com
![]() .
Este objeto
.
Este objeto
![]() é dito equalizador de f e g.
Claramente se vê que p é necessariamente um
monomorfismo.
é dito equalizador de f e g.
Claramente se vê que p é necessariamente um
monomorfismo.
Se J for
a categoria Transv
que tem apenas tres objetos
1, 2 e 3, e cujos únicos
morfismos fora as identidades são descritos por
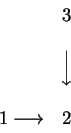
Limites nem sempre existem:
a categoria Cor de corpos não
tem produtos (um ``produto''
de corpos é um anel apenas, não é
um corpo). Quando existem
não são únicos: qualquer conjunto com
um único elemento
é um objeto final em Conj; mas dois limites
![]() e
e
![]() de
de
![]() são sempre isomorfos.
Com efeito,
são sempre isomorfos.
Com efeito,
![]() e
e
![]() devem satisfazer as propriedades
universais apropriadas;
por definição da propriedade universal
para
devem satisfazer as propriedades
universais apropriadas;
por definição da propriedade universal
para
![]() deve existir
deve existir
![]() satisfazendo as
propriedades de comutação e
analogamente para
satisfazendo as
propriedades de comutação e
analogamente para
![]() .
Estas composições
também irão satisfazer as propriedades
de comutação,
assim como obviamente as satisfazem as identidades
.
Estas composições
também irão satisfazer as propriedades
de comutação,
assim como obviamente as satisfazem as identidades
![]() e
e
![]() .
Agora invocamos a unicidade na
propriedade universal para concluir
que estas composições são isomorfismos.
.
Agora invocamos a unicidade na
propriedade universal para concluir
que estas composições são isomorfismos.
O conceito dual de limite é o do colimite:
dados uma categoria C,
uma categoria J
(a ser usada como índice) e um
funtor
![]() ,
um colimite
de
,
um colimite
de ![]() é um objeto
é um objeto
![]() em C
e para cada objeto i de J um morfismo
em C
e para cada objeto i de J um morfismo
![]() tal que para cada morfismo
tal que para cada morfismo
![]() temos
temos
![]() .
Estes dados devem obedecer
à seguinte propriedade universal:
para cada objeto X em C ao qual se associa,
para cada objeto i de J, um morfismo
.
Estes dados devem obedecer
à seguinte propriedade universal:
para cada objeto X em C ao qual se associa,
para cada objeto i de J, um morfismo
![]() tal que para cada morfismo
tal que para cada morfismo
![]() tenhamos
tenhamos
![]() deve existir um
único morfismo
deve existir um
único morfismo
![]() satisfazendo
satisfazendo
![]() para todo objeto i de J.
Colimites para funtores
tendo como domínios as categorias
2, Vaz,
Paral e Transv
são chamados coprodutos,
objetos iniciais,
coequalizadores e somas
fibradas, respectivamente.
Coprodutos existem em Top,
sendo a construção
da soma topológica de dois espaços,
em Conj, sendo a união
disjunta de dois conjuntos,
em
para todo objeto i de J.
Colimites para funtores
tendo como domínios as categorias
2, Vaz,
Paral e Transv
são chamados coprodutos,
objetos iniciais,
coequalizadores e somas
fibradas, respectivamente.
Coprodutos existem em Top,
sendo a construção
da soma topológica de dois espaços,
em Conj, sendo a união
disjunta de dois conjuntos,
em
![]() ,
sendo a soma externa
,
sendo a soma externa
![]() de dois
modulos sobre um anel A, e em
AnCom, a categoria de
aneis comutativos com unidade,
sendo o produto tensorial.
O conjunto vazio é objeto inicial
de Conj e de Top,
o anel dos inteiros
é objeto inicial de Anud.
Somas fibradas e coequalizadores
existem em Conj e em
Top. Como no caso de limites, os colimites,
quando existem,
são únicos a menos de isomorfismos.
de dois
modulos sobre um anel A, e em
AnCom, a categoria de
aneis comutativos com unidade,
sendo o produto tensorial.
O conjunto vazio é objeto inicial
de Conj e de Top,
o anel dos inteiros
é objeto inicial de Anud.
Somas fibradas e coequalizadores
existem em Conj e em
Top. Como no caso de limites, os colimites,
quando existem,
são únicos a menos de isomorfismos.
Os limites que existirem em uma categoria D
existirão em qualquer
categoria de funtores
![]() ,
e são calculados
``ponto a ponto'' da seguinte forma:
se
,
e são calculados
``ponto a ponto'' da seguinte forma:
se ![]() é uma
categoria índice para a qual
limites de funtores
é uma
categoria índice para a qual
limites de funtores
![]() existem então, para todo
objeto X de C,
a avaliação em X preserva
este limite, de tal modo que um funtor
existem então, para todo
objeto X de C,
a avaliação em X preserva
este limite, de tal modo que um funtor
![]() fornece por avaliação
em X um funtor
fornece por avaliação
em X um funtor
![]() tal que
tal que
![]() ,
cujo limite
existe por hipótese.
Estes limites se juntam em um limite para
,
cujo limite
existe por hipótese.
Estes limites se juntam em um limite para
![]() para o qual temos a equação escrita em D
para o qual temos a equação escrita em D
Uma categoria é dita completa (resp., cocompleta) se tiver todos os limites (resp., todos os colimites). A este respeito temos o
Teorema sobre a Existência de Limites.
A categoria C é completa se e só se
tiver produtos e equalizadores.
A prova mostra como construir o limite de um funtor
arbitrário
![]() a partir de produtos e de equalizadores. Para isso em
C consideramos o produto
P dos objetos
a partir de produtos e de equalizadores. Para isso em
C consideramos o produto
P dos objetos
![]() para cada objeto i de J,
e o produto Q dos
objetos
para cada objeto i de J,
e o produto Q dos
objetos
![]() para
cada morfismo
para
cada morfismo
![]() em J. Assim,
para cada objeto i de J temos
uma projeção
em J. Assim,
para cada objeto i de J temos
uma projeção
![]() e para
cada morfismo
e para
cada morfismo
![]() de J
temos uma
projeção
de J
temos uma
projeção
![]() .
Pela
universalidade do produto Q existe um
único morfismo
.
Pela
universalidade do produto Q existe um
único morfismo
![]() com
com
![]() e um único morfismo
e um único morfismo
![]() com
com
![]() para cada objeto i e cada
morfismo
para cada objeto i e cada
morfismo
![]() de J. O limite Lim
de J. O limite Lim
![]() então pode ser construido como o
equalizador de f e g.
então pode ser construido como o
equalizador de f e g.
Um esquema mnemônico para esta prova é o seguinte:
para
![]() o
o
![]() é o equalizador de
é o equalizador de
![]() ,
onde o primeiro produto é tomado
sobre os objetos j
de J e o segundo sobre os morfismos
,
onde o primeiro produto é tomado
sobre os objetos j
de J e o segundo sobre os morfismos
![]() de J
e, se
de J
e, se
![]() denota a projeção canônica,
então
denota a projeção canônica,
então
![]() .
.
Vale um enunciado dual para colimites, que podem ser
construidos através de coprodutos e coequalizadores.
Em Conj, por exemplo,
| (A.3.1) |
A categoria Conj
é completa, e, pelo visto acima,
também as categorias
![]() .
.
A.4. Funtores adjuntos.
Dado um funtor
![]() entre duas
categorias C e D,
diz-se que
entre duas
categorias C e D,
diz-se que
![]() preserva limites
se para cada limite
preserva limites
se para cada limite
![]() em C tivermos
em C tivermos
![]() .
O estudo sobre a preservação
de limites em funtores nos
leva ao conceito mais importante da teoria
de categorias: Um funtor
.
O estudo sobre a preservação
de limites em funtores nos
leva ao conceito mais importante da teoria
de categorias: Um funtor
![]() é adjunto à esquerda
de um funtor
é adjunto à esquerda
de um funtor
![]() se para cada
par de objetos
C em C e D em D
existir uma bijeção
(escrita em Conj)
se para cada
par de objetos
C em C e D em D
existir uma bijeção
(escrita em Conj)
| (A.4.1) |
Grande número de situações
familiares são exemplos de
adjunções. A propriedade
que caracteriza o produto tensorial
de módulos sobre um
anel A pode ser escrita como a existência
de uma bijeção natural
| (A.4.2) |
Na definição de funtor adjunto a naturalidade
(em C) de ![]() deve ser entendida da seguinte maneira:
dados objetos C e C' em
C e
deve ser entendida da seguinte maneira:
dados objetos C e C' em
C e
![]() vale a equação
escrita em
vale a equação
escrita em
![]()
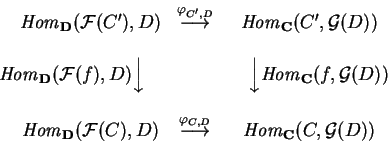
Um Teorema importante garante que um funtor adjunto à esquerda preserva colimites:
Teorema da Preservação de Limites.
Valem as seguintes situações
em que limites são
preservados.
1. Se
![]() tem adjunto à esquerda
(resp., à direita) e
tem adjunto à esquerda
(resp., à direita) e
![]() tem um limite
tem um limite
![]() (resp., um colimite
(resp., um colimite
![]() )
em C então
)
em C então
![]() (resp.,
(resp.,
![]() ).
).
2. Funtores representáveis preservam limites:
se C é
objeto de uma categoria C então
o funtor representável
![]() é
tal que, se
é
tal que, se
![]() tem um limite
tem um limite
![]() então
então
![]() .
.
3. Limites comutam com limites
(e colimites comutam com colimites),
isto é, se o funtor
![]() for definido por limites
então vale
for definido por limites
então vale
![]() .
Formalmente isto significa
que se
.
Formalmente isto significa
que se
![]() for funtor
em A e em J e se existirem os limites
for funtor
em A e em J e se existirem os limites
![]() ,
,
![]() e
e
![]() , então
, então
![]() , e analogamente para colimites.
, e analogamente para colimites.
4. Colimites não comutam necessariamente com
limites --
ao invés disto temos um morfismo natural
![]() , que nem sempre é isomorfismo.
No caso de um funtor
, que nem sempre é isomorfismo.
No caso de um funtor
![]() uma condição
suficiente para termos
uma condição
suficiente para termos ![]() isomorfismo é
a categoria I
ser finita e a categoria J
não ser vazia e satisfazer
isomorfismo é
a categoria I
ser finita e a categoria J
não ser vazia e satisfazer
4.i Para quaisquer objetos j, j' de
J temos
um objeto k de J e morfismos
![]() e
e
![]() .
.
4.ii Para quaisquer
morfismos paralelos
![]() existe um morfismo
existe um morfismo
![]() com
com
![]() .
.
Uma categoria safisfazendo as condições
em 4. é dita
filtrada.
Para provar 1. suponhamos, por exemplo, que
![]() tem adjunto
à direita
tem adjunto
à direita
![]() ,
tomamos o objeto
,
tomamos o objeto
![]() em D e mostremos que ele satisfaz à
propriedade universal de
colimite para
em D e mostremos que ele satisfaz à
propriedade universal de
colimite para
![]() .
Para isso consideremos um
objeto D em D tal que para cada
objeto i de J
tenhamos especificado um morfismo
.
Para isso consideremos um
objeto D em D tal que para cada
objeto i de J
tenhamos especificado um morfismo
![]() em
D tal que para cada morfismo
em
D tal que para cada morfismo
![]() em J
tenhamos
em J
tenhamos
![]() .
Aplicando
a bijeção
.
Aplicando
a bijeção
![]() dada pela
adjunção ao morfismo
ui obtemos
dada pela
adjunção ao morfismo
ui obtemos
![]() ,
e a naturalidade de
,
e a naturalidade de ![]() nos
objetos de C
garante que
nos
objetos de C
garante que
![]() para cada morfismo
para cada morfismo
![]() em J.
Pela universalidade
de
em J.
Pela universalidade
de
![]() existe um único
morfismo
existe um único
morfismo
![]() ao qual aplicamos
ao qual aplicamos
![]() obtendo um morfismo
obtendo um morfismo
![]() em D. Este
morfismo satisfaz as propriedades de
comutação apropriadas
e é único por naturalidade.
em D. Este
morfismo satisfaz as propriedades de
comutação apropriadas
e é único por naturalidade.
Para provar 2. aplicamos o funtor
![]() em
em
![]() ,
obtendo morfismos
,
obtendo morfismos
![]() por composição.
Para mostrar a universalidade
de
por composição.
Para mostrar a universalidade
de
![]() tomamos um outro objeto X em Conj com
morfismos
tomamos um outro objeto X em Conj com
morfismos
![]() ,
para cada objeto i de
J, satisfazendo as propriedades necessárias
de comutação. Cada elemento x de X
fornece um
morfismo
,
para cada objeto i de
J, satisfazendo as propriedades necessárias
de comutação. Cada elemento x de X
fornece um
morfismo
![]() em C,
também satisfazendo estas
comutações necessárias.
Por universalidade do limite
em C,
também satisfazendo estas
comutações necessárias.
Por universalidade do limite
![]() ,
existe
um único morfismo
,
existe
um único morfismo
![]() com
com
![]() .
Definimos então
.
Definimos então
![]() por k(x)=hx, e k é a
única definição possível
com
por k(x)=hx, e k é a
única definição possível
com
![]() ,
provando
a universalidade.
,
provando
a universalidade.
Para provar 3. construimos,
para cada objeto i de
I e cada objeto j de J,
o diagrama escrito em
C
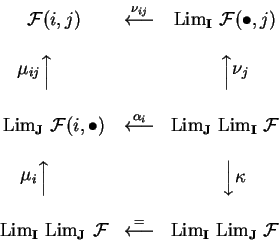
Para provar 4.
construimos o morfismo ![]() de modo
análogo ao de 3.,
com algumas setas invertidas:
de modo
análogo ao de 3.,
com algumas setas invertidas:
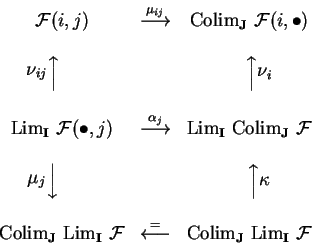
Suponhamos agora J
filtrada. Um elemento x
do limite
![]() é caracterizado,
como todo elemento de
um objeto de Conj, por um morfismo
é caracterizado,
como todo elemento de
um objeto de Conj, por um morfismo
![]() .
Para cada objeto
i de I tomamos a composta
.
Para cada objeto
i de I tomamos a composta
![]() ,
que é um elemento do
colimite
,
que é um elemento do
colimite
![]() .
Por
definição de limite, para um morfismo
.
Por
definição de limite, para um morfismo
![]() em
I devemos ter
em
I devemos ter
![]() ,
como elementos
em
,
como elementos
em
![]() .
Recordando a
construção de colimites
em Conj (A.3.1) vemos que este
elemento pode ser representado
por um elemento
.
Recordando a
construção de colimites
em Conj (A.3.1) vemos que este
elemento pode ser representado
por um elemento
![]() de
de
![]() ,
para algum j,
sujeito à equivalência descrita em
(A.3). Por 4.i,
a igualdade destes elementos em
,
para algum j,
sujeito à equivalência descrita em
(A.3). Por 4.i,
a igualdade destes elementos em
![]() pode ser testada em um
mesmo conjunto
pode ser testada em um
mesmo conjunto
![]() ,
e por 4.ii esta igualdade pode
ser testada pela aplicação
de um morfismo
,
e por 4.ii esta igualdade pode
ser testada pela aplicação
de um morfismo
![]() de J. Como I é finito,
este elemento x de
de J. Como I é finito,
este elemento x de
![]() pode ser representado por um elemento
pode ser representado por um elemento
![]() em
em
![]() que obedece, para cada morfismo
que obedece, para cada morfismo
![]() em I,
em I,
![]() .
Por definição, este é
um elemento do
.
Por definição, este é
um elemento do
![]() .
Tomando a imagem
deste elemento em
.
Tomando a imagem
deste elemento em
![]() ,
temos um aplicação
,
temos um aplicação
![]() bem
definida e natural, e inversa
do morfismo
bem
definida e natural, e inversa
do morfismo ![]() acima.
acima.
O funtor de esquecimento
![]() tem um adjunto à esquerda
tem um adjunto à esquerda
![]() que associa a cada conjunto X o
grupo livre
que associa a cada conjunto X o
grupo livre
![]() gerado
por X; o funtor
gerado
por X; o funtor
![]() é adjunto
à direita de
é adjunto
à direita de
![]() e logo preserva limites: isto explica
porque o produto de grupos
é construido sobre o produto
cartesiano dos conjuntos subjacentes
aos grupos. No entanto, o objeto
inicial de Grp é o
grupo trivial (só a identidade como
elemento; é também
objeto final em Grp), e
fazendo o funtor de esquecimento
agir neste objeto não obtemos o
objeto inicial de Conj
(que é o conjunto vazio).
Isto mostra que
e logo preserva limites: isto explica
porque o produto de grupos
é construido sobre o produto
cartesiano dos conjuntos subjacentes
aos grupos. No entanto, o objeto
inicial de Grp é o
grupo trivial (só a identidade como
elemento; é também
objeto final em Grp), e
fazendo o funtor de esquecimento
agir neste objeto não obtemos o
objeto inicial de Conj
(que é o conjunto vazio).
Isto mostra que
![]() não
preserva colimites, e portanto
não tem funtor adjunto à
direita.
não
preserva colimites, e portanto
não tem funtor adjunto à
direita.
O funtor de esquecimento
![]() tem um adjunto à esquerda
tem um adjunto à esquerda
![]() que associa a cada conjunto X o espaço
topológico dado pela
topologia discreta em X (tudo aberto),
e tem um adjunto à
direita
que associa a cada conjunto X o espaço
topológico dado pela
topologia discreta em X (tudo aberto),
e tem um adjunto à
direita
![]() que associa a
cada conjunto X o espaço topológico dado pela
topologia grosseira em X (só X e
que associa a
cada conjunto X o espaço topológico dado pela
topologia grosseira em X (só X e
![]() abertos).
Isto explica porque
abertos).
Isto explica porque
![]() preserva
limites e colimites de
Top: a topologia produto é
construida sobre o produto
cartesiano dos conjuntos subjacentes
aos espaços, e a soma topológica
é construida sobre
a soma (i.e., a união disjunta)
dos conjuntos subjacentes.
Assim, também como Conj,
a categoria Top
é completa e cocompleta.
preserva
limites e colimites de
Top: a topologia produto é
construida sobre o produto
cartesiano dos conjuntos subjacentes
aos espaços, e a soma topológica
é construida sobre
a soma (i.e., a união disjunta)
dos conjuntos subjacentes.
Assim, também como Conj,
a categoria Top
é completa e cocompleta.
Adjunções às vezes se
manifestam sem a interferência
dos conjuntos de morfismos, por exemplo,
das seguintes maneiras.
Podemos em (A.4.1), à maneira de Yoneda,
avaliar a bijeção
![]() na identidade
na identidade
![]() ,
obtendo
um morfismo
,
obtendo
um morfismo
![]() .
Esta
aplicação
.
Esta
aplicação ![]() é dita a
unidade da adjunção
em C. Como temos, para todo
morfismo
é dita a
unidade da adjunção
em C. Como temos, para todo
morfismo
![]() ,
o seguinte diagrama comutativo
escrito em Conj expressando a
naturalidade de
,
o seguinte diagrama comutativo
escrito em Conj expressando a
naturalidade de ![]()
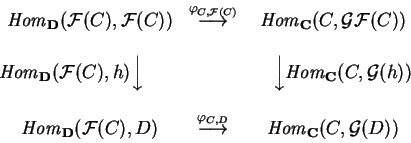
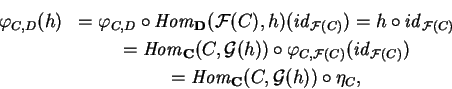
Uma adjunção pode ser
também determinada pelo dual da unidade,
a saber, a counidade
da adjunção, dada pela
aplicação de
![]() à unidade
à unidade
![]() do conjunto
de morfismos
do conjunto
de morfismos
![]() .
O argumento que mostra
isto, à maneira de Yoneda, é inteiramente dual.
.
O argumento que mostra
isto, à maneira de Yoneda, é inteiramente dual.
Se a unidade
![]() e a
counidade
e a
counidade
![]() de uma adjunção forem
isomorfismos naturais então
de uma adjunção forem
isomorfismos naturais então
![]() (ou
(ou
![]() )
definem uma equivalência de categorias,
e vale a recíproca.
Neste caso,
)
definem uma equivalência de categorias,
e vale a recíproca.
Neste caso,
![]() é tanto o adjunto à esquerda
de
é tanto o adjunto à esquerda
de
![]() por uma
adjunção cuja unidade é
por uma
adjunção cuja unidade é ![]() quanto
o adjunto à direita
de
quanto
o adjunto à direita
de
![]() por uma adjunção cuja unidade
é
por uma adjunção cuja unidade
é
![]() .
.
A.5. Espaços sob e sobre espaço.
Seja C um objeto de uma categoria C. A
categoria ![]() de espaços sobre C
tem por objetos elementos
de espaços sobre C
tem por objetos elementos
![]() e
os morfismos entre
e
os morfismos entre
![]() e
e
![]() são dados por
elementos
são dados por
elementos
![]() que
satisfazem
que
satisfazem
![]() .
De maneira dual a categoria
.
De maneira dual a categoria ![]() de espaços sob C
tem por objetos elementos
de espaços sob C
tem por objetos elementos
![]() e
os morfismos entre
e
os morfismos entre
![]() e
e
![]() são dados
por elementos
são dados
por elementos
![]() que satisfazem
que satisfazem
![]() .
Tanto
.
Tanto ![]() quanto
quanto ![]() admitem naturalmente
funtores de esquecimento
admitem naturalmente
funtores de esquecimento
![]() e
e
![]() levando
o objeto
levando
o objeto
![]() em
X
e o morfismo
em
X
e o morfismo
![]() em
h.
em
h.
A identidade
![]() é objeto final
de
é objeto final
de ![]() e objeto inicial de
e objeto inicial de
![]() .
Os funtores
.
Os funtores
![]() e
e
![]() levam naturalmente
levam naturalmente
![]() em
C, o que mostra que
em
C, o que mostra que
![]() (respectivamente,
(respectivamente,
![]() )
não tem em geral adjunto
à esquerda (respectivamente,
à direita). Se, no entanto, C tiver
coprodutos finitos (isto é,
colimites para funtores vindo de categorias
com finitos objetos e
sem morfismos que não sejam identidades)
então
)
não tem em geral adjunto
à esquerda (respectivamente,
à direita). Se, no entanto, C tiver
coprodutos finitos (isto é,
colimites para funtores vindo de categorias
com finitos objetos e
sem morfismos que não sejam identidades)
então
![]() tem um adjunto à esquerda que associa
a cada objeto X de
tem um adjunto à esquerda que associa
a cada objeto X de
![]() o objeto de
o objeto de ![]() dado por
dado por
![]() (onde
(onde ![]() denota o coproduto de X e C).
A bijeção natural
denota o coproduto de X e C).
A bijeção natural ![]() que define
a adjunção
associa a cada morfismo
que define
a adjunção
associa a cada morfismo
![]() de C
a aplicação única
de C
a aplicação única
![]() dada pela
propriedade universal do coproduto.
De maneira dual, se C
tiver produtos finitos então
dada pela
propriedade universal do coproduto.
De maneira dual, se C
tiver produtos finitos então
![]() tem um adjunto à
direita que associa a cada objeto X
de C o objeto de
tem um adjunto à
direita que associa a cada objeto X
de C o objeto de
![]() dado pela projeção
dado pela projeção
![]() .
Isto mostra que as categorias
.
Isto mostra que as categorias
![]() e
e
![]() são completas, e que as categorias
são completas, e que as categorias
![]() e
e
![]() são cocompletas.
são cocompletas.
Se C possui produtos fibrados (respectivamente,
somas fibradas) então tanto ![]() quanto
quanto
![]() possuem estes produtos (resp., somas) e
tanto
possuem estes produtos (resp., somas) e
tanto
![]() quanto
quanto
![]() preservam estes
produtos (resp., somas). No caso de produtos,
por exemplo, consideramos
os morfismos
preservam estes
produtos (resp., somas). No caso de produtos,
por exemplo, consideramos
os morfismos
![]() e
e
![]() entre os objetos
entre os objetos
![]() de
de
![]() ,
para
i=1,2,3; temos o produto fibrado
,
para
i=1,2,3; temos o produto fibrado
![]() de
f1 e f2 em C dado com
de
f1 e f2 em C dado com
![]() para i=1,3.
Tomando o produto fibrado
para i=1,3.
Tomando o produto fibrado
![]() de g1
e g3 e
sua universalidade obtemos
de g1
e g3 e
sua universalidade obtemos
![]() e a composta
e a composta
![]() será vista como
o objeto
será vista como
o objeto
![]() de
de ![]() .
Para testar nesta composta a
propriedade universal tomamos um objeto
.
Para testar nesta composta a
propriedade universal tomamos um objeto
![]() de
de ![]() e morfismos
e morfismos
![]() e
e
![]() em
em ![]() (de modo que
(de modo que
![]() para i=1,3) satisfazendo comutações
(de modo que
para i=1,3) satisfazendo comutações
(de modo que
![]() em
em ![]() );
pela universalidade
de
);
pela universalidade
de
![]() em C
existe um único morfismo
em C
existe um único morfismo
![]() em C satisfazendo
em C satisfazendo
![]() para i=1,3. Devemos mostrar que
u é morfismo em
para i=1,3. Devemos mostrar que
u é morfismo em ![]() ,
mas isto é
consequência de
,
mas isto é
consequência de
![]() .
.
Um argumento análogo mostra que se C
tem coequalizadores
então ![]() também os tem e
também os tem e
![]() os preserva:
dados objetos
os preserva:
dados objetos
![]() e
e
![]() em
em ![]() e morfismos
e morfismos
![]() em
em ![]() tomamos o coequalizador
tomamos o coequalizador
![]() em C.
Como m e n são morfismos em
em C.
Como m e n são morfismos em ![]() temos
temos
![]() ,
e usando
a universalidade do
coequalizador temos que existe um único morfismo
,
e usando
a universalidade do
coequalizador temos que existe um único morfismo
![]() com
com
![]() ,
e logo
,
e logo
![]() é coequalizador
em
é coequalizador
em ![]() .
A universalidade de um coproduto
.
A universalidade de um coproduto
![]() que existir em C mostra que o coproduto também
será um objeto de
que existir em C mostra que o coproduto também
será um objeto de ![]() ,
e também
coproduto lá.
Isto mostra que
,
e também
coproduto lá.
Isto mostra que
![]() e
e
![]() são cocompletas.
são cocompletas.
Se C for objeto inicial
(respectivamente, final) de C
então ![]() (resp.,
(resp., ![]() )
se reduz a C.
Por exemplo, em Conj o conjunto
)
se reduz a C.
Por exemplo, em Conj o conjunto ![]() com
um só elemento é objeto final, e logo
com
um só elemento é objeto final, e logo
![]() é Conj, mas
é Conj, mas
![]() é
a categoria de conjuntos com um ponto base
e analogamente
para
é
a categoria de conjuntos com um ponto base
e analogamente
para
![]() .
.
Se C possui produtos fibrados
(resp., somas fibradas)
e
![]() é morfismo
em C então o
funtor
é morfismo
em C então o
funtor
![]() (resp.,
(resp.,
![]() )
que a cada objeto
)
que a cada objeto
![]() de
de ![]() (resp.,
(resp.,
![]() de
de
![]() )
associa
o produto fibrado
)
associa
o produto fibrado
![]() (resp., a soma
fibrada
(resp., a soma
fibrada
![]() )
tem um adjunto à esquerda
)
tem um adjunto à esquerda ![]() (resp., um adjunto à direita
(resp., um adjunto à direita ![]() )
dado pela composição com f à esquerda
(resp., à direita):
)
dado pela composição com f à esquerda
(resp., à direita):
| (A.5.1) |
| (A.5.2) |
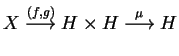 ,
(aqui
,
(aqui
O conceito dual de co-objeto de
Hopf em categorias que tenham coprodutos
significa um objeto H de C
para o qual existe um morfismo
![]() que faz com que para todo objeto X de C,
que faz com que para todo objeto X de C,
![]() tenha uma estrutura
de grupo, natural em X, dada pela seguinte regra:
para morfismos
tenha uma estrutura
de grupo, natural em X, dada pela seguinte regra:
para morfismos
![]() então a operação
é definida por
então a operação
é definida por
![]() Desta maneira temos um funtor de
esquecimento covariante
Desta maneira temos um funtor de
esquecimento covariante
![]() representado por H.
representado por H.
Para um objeto de Hopf H em C
a naturalidade da
estrutura de grupo no conjunto
![]() significa
que para um morfismo
significa
que para um morfismo
![]() a função
a função
![]() é um homomorfismo de grupos.
é um homomorfismo de grupos.
Como
![]() tem estrutura de grupo
existe um morfismo
tem estrutura de grupo
existe um morfismo
![]() que é
a unidade deste grupo, caracterizado
pela comutatividade
do diagrama escrito em C
que é
a unidade deste grupo, caracterizado
pela comutatividade
do diagrama escrito em C
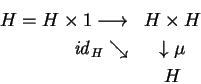
Um objeto de Hopf H
é dito abeliano se for
comutativo o seguinte diagrama
escrito em C onde
o morfismo horizontal ![]() é a troca
de coordenadas
é a troca
de coordenadas
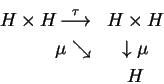
Topólogos identificaram pela primeira
vez objetos e co-objetos de Hopf, na categoria
![]() de classes de homotopia
de espaços topógicos com um ponto-base,
sob a denominação H grupos e
H cogrupos
(ver, por exemplo, [Sp], que
inclui os axiomas de co-objeto de
Hopf na página 40).
de classes de homotopia
de espaços topógicos com um ponto-base,
sob a denominação H grupos e
H cogrupos
(ver, por exemplo, [Sp], que
inclui os axiomas de co-objeto de
Hopf na página 40).