Representações

O conceito bastante geral de representação para grupos foi definido no exemplo 3. em I.3:

$$\rho:G\longrightarrow {\it Aut}_{\bf C}(C,C).$$

Se C for uma categoria de módulos com alguma estrutura então a representação linear $\rho$ e o módulo C costumam ser identificados. Assim, por exemplo, se G for um grupo de Lie então em I.2 foi visto que Ad é uma representação de G em sua álgebra de Lie $\mathcal{ L}(G)=D(G)_I$, como um espaço vetorial, isto é, ${\bf C}=Vect_k$ é a categoria dos espaços vetoriais sobre k. Uma tal representação linear é simplesmente um morfismo de grupos $\rho:G\rightarrow Gl(V)$.

Naturalmente se generaliza este conceito para outras categorias. Assim, para uma álgebra de Lie A uma representação é um morfismo $\rho:A\rightarrow gl(V)$ de álgebras de Lie. Uma representação de um grupo de Lie G dá origem a uma representação de sua álgebra de Lie $\mathcal{ L}(G)$ por derivação, e localmente vale uma recíproca. Se G for conexo e simplesmente conexo as representações em dimensão finita de G e de $\mathcal{ L}(G)$ se correspondem bijetivamente.

Para uma álgebra A sobre k, objeto de ${\bf Alg}_k$, uma representação é um morfismo $\rho:A\rightarrow {\it Hom}_k(V,V)$. Para uma álgebra de Lie A sobre k as representações de A correspondem bijetivamente às representações de sua álgebra envolvente $\mathcal{ U}(A)$.

Para um funtor $G:{\bf C}\rightarrow {\bf Grp}$ em grupos e um funtor $X:{\bf C}\rightarrow {\bf Conj}$ em conjuntos uma representação é uma transformação natural $G\times X\stackrel{\bullet}{\rightarrow} X$ que a cada objeto C define uma ação $G(C)\times X(C)\rightarrow X(C)$. No caso tartado em (I.3) acima ${\bf C}={\bf AlgCom}_k$, e a representação é linear se para toda álgebra A, objeto de ${\bf AlgCom}_k$, $X(A)=V\times A$, para um módulo V sobre k fixo, e se G(A) é linear sobre k. Se os funtores forem representáveis, observando o que estes dados implicam para os objetos que os representam, à maneira de Yoneda, é natural a definição: se A é um objeto de Hopf em ${\bf AlgCom}_k$ um módulo V sobre k é dito um comódulo sobre A se existir $\rho:V\rightarrow V\otimes A$ tornando comutativos os diagramas

$$\begin{matrix}V& \mathop{\longrightarrow} \limits^{\rho} &... ...limits^{\rho\otimes\Delta} &V\otimes A\otimes A, \end{matrix}$$

e

$$\begin{matrix}V& \mathop{\longrightarrow} \limits^{\rho} &... ...{\longrightarrow} \limits^{\simeq} &V\otimes k. \end{matrix}$$

Se V=A e $\rho=\Delta$ temos a representação regular de A.

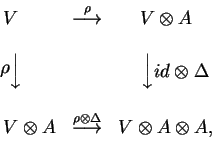
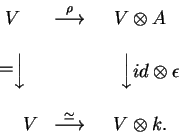
Exemplos e Exercícios

1. O caso de Sl₂. Representações da álgebra de Lie $sl_2=\mathcal{ L}(Sl_2)$ correspondem a representações de sua álgebra envolvente $\mathcal{ UL}(sl_2)$. Representações irredutíveis de dimensão finita de $\mathcal{ UL}(sl_2)$ são parametrizadas por naturais da seguinte maneira. Lembramos (1. depois de ( I.4)) que $\mathcal{ UL}(sl_2)$ é gerada por X,Y e H; dado um módulo V sobre $\mathcal{ UL}(sl_2)$, um autovetor $v\in V$ de H

$$Hv=\lambda v$$

é dito ter peso $\lambda$. (Aqui se identifica H com $\rho (H)$). Se, além disso, Xv=0 então v é dito ser vetor de peso máximo.

Sobre um corpo algebricamente fechado k todo módulo tem vetor de peso máximo: certamente existirá um autovetor v de H com autovalor $\alpha$, e se Xv=0 ele será vetor de peso máximo. Caso contrário, considere-se a sequência Xⁱ(v). Pelas relações listadas em 1. de (I.4) (válidas também em $\mathcal{ U}(sl_2({\bf C}))$) vale

$$HX^i(v)=(\alpha +2i)X^iv,$$

e logo Xⁱv são autovetores de H com autovalores distintos. Como o módulo tem dimensão finita, eventualmente acontece que $X^iv\not= 0$ mas Xⁱ⁺¹v=0, e neste caso Xⁱv é vetor de peso máximo. Destas relações ainda se deduz, para v vetor de peso máximo com peso $\lambda$,

$$H\frac{Y^iv}{i!}=(\lambda -2i)\frac{Y^iv}{i!},$$

$$X\frac{Y^iv}{i!}=(\lambda -i+1) \frac{Y^{i-1}v}{(i-1)!}$$

e

$$Y\frac{Y^iv}{i!}=(i+1)\frac{Y^{i+1}v}{(i+1)!}.$$

Assim, $\{ \frac{Y^iv}{i!}\}$ é uma sequência de autovetores de H com autovalores distintos e, novamente, deve existir um maior inteiro i para o qual $\frac{Y^iv}{i!}$ não seja nulo. De fato, pelas relações acima $0=X\frac{Y^{i+1}v} {(i+1)!}= (\lambda -i)\frac{Y^iv}{i!}$, e logo $\lambda =i$ é um inteiro. Além disso, $\{ \frac{Y^jv}{j!}\}_{j=0, \ldots ,\lambda}$ é conjunto linearmente independente, uma vez que são autovetores associados de H a distintos autovalores. O módulo que estes vetores geram tem assim dimensão $\lambda +1$ e é simples, e a ação de H é diagonal com $\lambda +1$ autovalores distintos $\lambda, \lambda-2,\ldots ,\lambda- 2\lambda =-\lambda$. O vetor de peso máximo é distinguido entre os autovetores por estar associado ao autovalor $\lambda$, de modo que qualquer outro vetor de peso máximo é um múltiplo escalar de v. Como qualquer módulo tem um vetor de peso máximo, os únicos módulos simples V (de dimensão finita) de $\mathcal{ U}(sl_2({\bf C}))$ são os módulos gerados por um vetor de peso máximo de peso inteiro $i=\dim V$. Este módulo é dito módulo de peso máximo e é denotado por V(i), com a representação correspondente denotada por $\rho_i:sl_2({\bf C})\rightarrow gl_{i+1} ({\bf C})$.

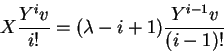
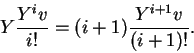
Observe que $\rho_0$ é a representação trivial, $\rho_1$ é a representação natural $sl_2\rightarrow gl_2$ e $\rho_2$ é a representação adjunta com X sendo o vetor de peso máximo, -H=[Y,X] e $Y=\frac{[Y,[Y,X]]}{2!}=-\frac{[Y,H]}{2!}$.

No módulo V(i) qualquer elemento do centro de $\mathcal{ U}(sl_2({\bf C}))$ age por um múltiplo escalar da identidade. Em particular, como para v o vetor de peso máximo e C o elemento de Casimir vale

$$Cv=XYv=YXv+\frac{H^2v}{2}=iv+\frac{i^2}{2}v,$$

o elemento de Casimir age por multiplicação por $\frac{i(i+2)}{2}$.