Álgebras de Lie e Álgebras Envolventes

Tal como definidas em I.2, as álgebras de Lie formam naturalmente uma categoria AlgLie, que já foi invocada naquela seção. Morfismos de álgebras de Lie são as transformações lineares que preservam as operações $[\bullet,\bullet]$, ideais (núcleos de morfismos) em uma álgebra de Lie V são subálgebras J tais que $[J,V]\subset J$ e em geral esta categoria funciona confortadoramente próxima da categoria AnCom.

Uma álgebra de Lie V é abeliana se [V,V]=0. Todo espaço vetorial pode ser dotado de uma estrutura de álgebra de Lie abeliana definindo a operação $[\bullet,\bullet]$ desta maneira trivial. Mais interessante, para toda espaço vetorial V sobre k o conjunto das transformações lineares ${\it Hom}_k(V,V)$ tem naturalmente a estrutura de álgebra de Lie com a definição

[A,B]=AB-BA.

Por causa do exemplo 1. em I.2, em que esta definição aparece como a álgebra de Lie $\mathcal{ L}(Gl_n({\bf R}))$, esta álgebra de Lie é denotada gl(V). Mais geralmente, cada álgebra (associativa) A sobre k origina uma álgebra de Lie gl(A) definindo, para $a,b\in A$,

[a,b]=ab-ba.

Assim, $gl(V)=gl({\it Hom}_k(V,V))$.

Esta associação define um funtor

$$gl:{\bf Alg}_k\longrightarrow {\bf AlgLie}_k.$$

(A notação ${\bf Alg}_k$ designa a categoria de álgebras associativas, mas não necessariamente comutativas, sobre k). Se A, objeto de ${\bf Alg}_k$, for comutativa então gl(A) é abeliana.

Este funtor gl tem um adjunto à esquerda, geralmente denotado por $\mathcal{ U}$ por lembrar ``universal'', diretamente ligado ao Teorema de Poincaré-Birkhoff-Witt. Para uma álgebra de Lie A define-se uma álgebra associativa $\mathcal{ U}(A)$ denominada a álgebra envolvente ou a álgebra envolvente universal de A, da seguinte maneira. Sobre o espaço vetorial subjacente de A (que será denotado confusamente pela mesma letra A), é tomada a álgebra tensorial

$$T=\oplus_{i\ge 0} T^i,\qquad {\rm onde} \ T^i=\otimes_{1\le j\le i} A.$$

Em T é considerado o ideal bilateral J gerado por $a\oplus b-b\oplus a-[a,b]$ para todos os pares $(a,b)\in A\times A$, e a álgebra envolvente é definida como uma álgebra quociente por $\mathcal{ U}(A)=T/J$. Como morfismo de espaços vetoriais existe um mergulho canônico $A\rightarrow T\rightarrow \mathcal{ U}(A)$. A adjunção

$$\mathcal{ U}:{\bf AlgLie}_k\leftrightarrow {\bf Alg}_k:gl$$

se expressa por

$${\it Hom}_{{\bf Alg}_k}(\mathcal{ U}(A),B) \stackrel {\simeq}{\longrightarrow} {\it Hom}_{{\bf AlgLie}_k}(A,gl(B)).$$

A verificação é imediata.

O Teorema de Poincaré-Birkhoff-Witt garante mais do que esta adjunção: mostra como construir uma base de $\mathcal{ U}(A)$ a partir de uma base de A (de dimensão não necessariamente finita).

Sendo adjunto à esquerda o funtor $\mathcal{ U}$ naturalmente preserva colimites (ver (A.4)). Assim vale, para álgebras de Lie A e B, que são isomorfas em ${\bf Alg}_k$ as álgebras

$$\varphi: \mathcal{ U}(A\oplus B)\stackrel{\simeq} {\longrightarrow} \mathcal{ U}(A)\otimes \mathcal{ U}(B).$$

Dada uma álgebra de Lie A aplicando o funtor $\mathcal{ U}$ ao morfismo diagonal

$$\begin{eqnarray*}\delta:A&\longrightarrow A\oplus A\\ a&\mapsto (a,a) \end{eqnarray*}$$

e depois compondo com o isomorfismo $\varphi$ definido acima resulta em um morfismo

$$\varphi\circ \mathcal{ U}(\delta):\mathcal{ U} (A)\longrightarrow \mathcal{ U}(A)\otimes \mathcal{ U}(A).$$

Este morfismo resultante satisfaz a propriedade co-associativa necessária para defini-lo como uma co-multiplicação $\delta =\varphi\circ \mathcal{ U}(\delta)$ que é essencialmente a diagonal. Por outro lado, o espaço vetorial trivial $\{ 0\}$, objeto inicial e final em ${\bf Vect}_k$, é trivialmente uma álgebra de Lie que é objeto inicial e final em ${\bf AlgLie}_k$. Aplicando $\mathcal{ U}$ ao único morfismo $A\rightarrow 0$ obtemos um morfismo $\epsilon:\mathcal{ U}(A) \rightarrow k$ que é compatível com a co-multiplicação $\Delta$ definida acima.

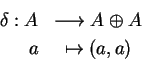
A categoria ${\bf AlgLie}_k$ admite um processo de dualização: a cada álgebra de Lie A pode ser considerada a álgebra oposta A^op definida sobre o mesmo espaço subjacente com a operação

[a,b]^op=[b,a]=-[a,b].

As álgebras A e A^op são isomorfas pelo isomorfismo $\omega:a\mapsto -a$. Aplicando $\mathcal{ U}$ a $\omega$ obtemos um morfismo $S=\mathcal{ U}(\omega)$ que é compatível com a co-multiplicação $\Delta$ e com a co-unidade $\epsilon$ definidas acima, e logo a álgebra envolvente $\mathcal{ U}(A)$ tem uma estrutura natural de álgebra de Hopf, agora não mais comutativa. álgebras de Hopf sobre k (não necessariamente comutativas) formam naturalmente uam categoria ${\bf AlgHopf}_k$, e existe, como em (I.3.1) um funtor de esquecimento

$$\mathcal{ E}_{\bf Hopf}:{\bf AlgHopf}_k \longrightarrow {\bf Alg}_k.$$

A operação descrita acima define um funtor

$$\mathcal{ H}:{\bf AlgLie}_k\longrightarrow {\bf AlgHopf}_k.$$

Para uma álgebra de Lie A a álgebra de Hopf $\mathcal{ H}(A)$ não é, em geral comutativa, já que a multiplicação em $\mathcal{ U}(A)$ é essencialmente o produto tensorial, que não tem porque comutar. No entanto $\mathcal{ H}(A)$ é co-comutativa, isto é, o diagrama abaixo é comutativo, onde $\tau$ é troca de coordenadas

$$\begin{eqnarray*}\mathcal{ H}(A)\times \mathcal{ H}(A) \mathop{\longrightarrow}... ...(A)\\ \Delta \nwarrow &\uparrow \Delta \\ &\mathcal{ H}(A). \end{eqnarray*}$$

A comutatividade deste diagrama é consequência da definição de $\mathcal{ H}$ e da comutatividade de

$$\begin{eqnarray*}A\oplus A \mathop{\longrightarrow}\limits^{\tau} & A\oplus A\\ \delta \nwarrow &\uparrow \delta \\ &A, \end{eqnarray*}$$

onde, aqui também, $\tau$ é (outra) troca de coordenadas.

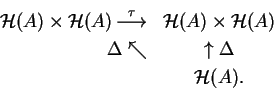
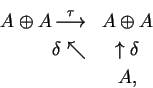
Exemplos e Exercícios

1. O caso de Sl₂. Algebricamente Sl₂ é um funtor representável ${\bf AlgCom}_k \rightarrow {\bf Grp}$, representado pela álgebra de Hopf comutativa mas não co-comutativa

A=k[X₁₁,X₁₂,X₂₁,X₂₂] /(1-(X₁₁X₂₂-X₁₂X₂₁))

com co-multiplicação, co-unidade e antípoda dado no exemplo 1. de I.3.

Geometricamente, pelo menos para $k={\bf R}$ o grupo $Sl_2({\bf R})$ é um grupo de Lie, e como tal tem associado sua álgebra de Lie $\mathcal{ L}(Sl_2({\bf R}))=sl_2({\bf R})$, calculada no exemplo 2. de I.2. Tomando a álgebra envolvente

$$\mathcal{ UL}(Sl_2({\bf R}))=\mathcal{ U}(sl_2({\bf R})$$

temos uma álgebra de Hopf $\mathcal{ H}(sl_2({\bf R}))$, co-comutativa mas não comutativa. Naturalmente se coloca o problema de investigar a relação entre A e $\mathcal{ H}(sl_2({\bf R})$. De fato, estas álgebras são duais uma da outra.

A álgebra envolvente $\mathcal{ U}(sl_2({\bf R}))$ é gerada pelos elementos

$$X:=\begin{pmatrix}0&1\\ 0&0\end{pmatrix},\qquad Y:=\begin{pm... ...matrix},\ {\rm e} \ H:=\begin{pmatrix}1&0\\ 0&-1\end{pmatrix}.$$

Valem as relações em $\mathcal{ U}(sl_2({\bf R}))$
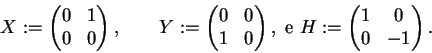
$$\begin{align}[X,Y]=H,\qquad [H,X]&=2X,\qquad [H,Y]=-2Y,\notag\\ X^iH^j=(H-2i)^... ... [X,Y^i]=iY^{i-1}(H-i+1), & \qquad [X^i,Y]=iX^{i-1}(H+i-1).\notag \end{align}$$
Como espaço vetorial $\mathcal{ U}(sl_2({\bf R}))$ admite a base

$$\{ X^iY^jH^k\ \vert\ i,j,k\in {\bf N}\ \}.$$

O centro de $\mathcal{ U}(sl_2({\bf R}))$ é gerado, como álgebra, pelo elemento de Casimir

$$C=XY+YX+\frac{H^2}{2}.$$

2. Mecânica algébrica na categoria ${\bf AlgHopf}_k$. Uma álgebra A, objeto de ${\bf Alg}_k$, é um espaço vetorial dotado de morfismos

$$\mu:A\otimes A\longrightarrow A,\qquad u:k\longrightarrow A.$$

Se A tiver dimensão finita então o espaço vetorial dual $A^*={\it Hom}_k (A,k)$ não tem uma estrutura de ágebra, mas uma de co-álgebra, isto é, um espaço vetorial dotado de morfismos

$$\Delta:A\longrightarrow A\otimes A,\qquad \epsilon:A\longrightarrow k.$$

Estes morfismos são chamados de co-multiplicação e de co-unidade, respectivamente. Co-álgebras, claro, definem uma categoria ${\bf CoAlg}_k$.

Uma álgebra A que é uma co-álgebra é algo interessante quando a multiplicação $\mu$ e a unidade u forem morfismos de co-álgebras, e isto acontece exatamente a co-multiplicação $\Delta$ e a co-unidade forem morfismos de álgebras. Neste caso a álgebra é dita uma bi-álgebra.

O morfismo que troca componentes em um produto tensorial será denotado por $\tau:A\otimes A \rightarrow A\otimes A$. Se A é bi-álgebra então A^op á a bi-álgebra que tem como multiplicação $\mu\circ \tau$, e as outras operações como A, A^cop é a bi-álgebra que tem como co-multiplicação $\tau\circ \Delta$, e as outras operações como A, e $A^{op\ cop}$ é a bi-álgebra que tem como multiplicação $\mu\circ \tau$, como co-multiplicação $\tau\circ \Delta$, e as outras operações como A. O dual de uma bi-álgebra tem uma estrutura de bi-álgebra.

Álgebras de Hopf são bi-álgebras que admitem um antípoda S. O dual de uma álgebra de Hopf de dimensão finita com antípoda S é uma álgebra de Hopf com antípoda S^*, a adjunta linear de S. Em uma álgebra de Hopf H, o antípoda é um morfismo de bi-álgebras

$$S:H\longrightarrow H^{op\ cop}.$$

Não é sempre verdade que S²=id; isto se passa exatamente quando para todo $x\in H$ vale

$$\mu\circ (S,id)\circ \Delta (x)=\epsilon(x).1,$$

que á equivalente a exigir que para todo $x\in H$ vale

$$\mu\circ (id,S)\circ \Delta (x)=\epsilon(x).1.$$

Se H for comutativa, isto é, se

$$\mu\circ\tau=\mu,$$

ou se H for co-comutativa, isto é, se

$$\tau\circ\Delta=\Delta,$$

então estas condições são satisfeitas.

Estes jogos de contas de vidro prosseguem indefinidamente: para uma álgebra de Hopf H a bi-álgebra $H^{op\ cop}$ é álgebra de Hopf com multiplicação $\mu\circ \tau$ e co-multiplicação $\tau\circ \Delta$, o antípoda S sendo morfismo de álgebra de Hopf.

A hipótese de dimensão finita, duas vezes formulada na discussão acima, é necessária. Uma co-álgebra C com co-multiplicação $\Delta$ traz naturalmente para seu dual linear $C^*={\it Hom}_k (C,k)$ uma estrutura de álgebra através da adjunta $\Delta^*:(A\otimes A)^* \rightarrow A^*$ de $\Delta$, depois da restrição de $(A\otimes A)^*$ a $A^*\otimes A^*$. Analogamente, se $\epsilon :A\rightarrow k$ é co-unidade então $\epsilon^*:k\rightarrow A^*$ é uma identidade para A^*. No entanto, se A é álgebra com multiplicação $\mu$, nem sempre $\mu^*$ dota A^* de uma estrutura de co-álgebra: o problema é que a imagem de uma co-multiplicação $\Delta:a\mapsto \sum_i a_i\otimes b_i$ deve ser tal que o somatório seja uma operação finita; isto acontece se A tiver dimensão finita.

3. Grupos de Chevalley. O material aqui reunido adiciona algo mais ao assunto da classificação de grupos simples finitos.

O contexto será a categoria ${\bf AlgLie}_k$ de álgebras de Lie, e o ponto de vista será cada vez mais algébrico, começando com o caso $k={\bf C}$. Em I.2 foi visto que $ad:D(G)_I\rightarrow {\it Hom}_k (D(G)_I,D(G)_I)$ é um homomorfismo em ${\bf AlgLie}_k$ da álgebra de Lie $D(G)_I=\mathcal{ L}(G)$ associada a um grupo de Lie G. Em geral, para uma álgebra de Lie $\mathcal{ L}$, objeto de ${\bf AlgLie}_k$, cada elemento $X\in \mathcal{ L}$ define uma aplicação $ad(X):\mathcal{ L}\rightarrow \mathcal{ L}$ por $ad(X):Y\mapsto [X,Y]$. Esta aplicação é linear mas não é morfismo em ${\bf AlgLie}_k$: ao invés, a identidade de Jacobi mostra que

ad(X)([Y,Z])=[X,[Y,Z]]=[[X,Y],Z]+[Y,[X,Z]]= [ad(X)(Y),Z]+[Y,ad(X)(Z)],

algo como a regra de Leibniz para derivações. Assim definimos uma derivação de $\mathcal{ L}$ como sendo uma aplicação linear $\delta:\mathcal{ L}\rightarrow \mathcal{ L}$ satisfazendo

$$\delta([X,Y])=[\delta(X),Y]+[X,\delta(Y)].$$

Assim, para todo $X\in \mathcal{ L}$ a aplicação ad(X) é uma derivação de $\mathcal{ L}$.

Sobre um corpo k de característica zero uma derivação $\delta$ nilpotente, isto é, tal que $\delta^n =0$ para algum n, gera um automorfismo

$$exp(\delta):=1+\delta+\delta^2/2!+\cdots +\delta^{n-1}/(n-1)!$$

de $\mathcal{ L}$. De fato, por indução se mostra

$$\delta^r([X,Y])=\sum_{0\le i\le r} \binom{r}{i}[\delta^i(X),\delta^{r-i}(Y)],$$

e logo

$$\frac{\delta^r([X,Y])}{r!}=\sum_{0\le i\le r} [\frac{\delta^i(X)}{i!}, \frac{\delta^{r-i}(Y)}{(r-i)!}].$$

Assim,
$$\begin{align}exp(\delta)[X,Y]&= \sum_{r\ge 0}\sum_{i+j=r} [\frac{\delta^i(X)}{... ...elta^j(Y)}{j!}]notag\\ &= [exp(\delta)(X),exp(\delta)(Y)].\notag \end{align}$$
O que se usa agora é o início da teoria clássica de álgebras de Lie simples, isto é, aquelas que não tem ideais (no sentido de álgebras de Lie) não triviais (ver [Hu]). Tais álgebras foram classificadas por Cartan e por Killing, e nesta classificação é crucial o papel desempenhado pelas subálgebras de Cartan: tais subálgebras são as subálgebras nilpotentes maximais, isto é, subálgebras $\mathcal{ H}\subset \mathcal{ L}$ tais que

$$[\cdots [[\mathcal{ H},\mathcal{ H}], \mathcal{ H}],\cdots ,\mathcal{ H}]=0,$$

onde a operação $[\mathcal{ H},\mathcal{ H}]$ à esquerda foi tomada um número finito de vezes, e tais que se $[X,H]\in \mathcal{ H}$ para todo $H\in \mathcal{ H}$ então $X\in \mathcal{ H}$, isto é, $\mathcal{ H}$ não é ideal de nenhuma subálgebra de $\mathcal{ L}$ propriamente contendo $\mathcal{ H}$.

Por exemplo, nas álgebras de Lie $\mathcal{ L}= sl_n(k)$ de matrizes $n\times n$ de traço nulo uma subálgebra de Cartan é dada pelo conjunto $\mathcal{ H}$ das matrizes $n\times n$ diagonais de traço nulo. Esta subálgebra tem dimensão $\dim (\mathcal{ H})=n-1$, e em geral a dimensão de uma subálgebra de Cartan $\mathcal{ H}\subset \mathcal{ L}$ é dito o posto de $\mathcal{ L}$: este conceito é bem definido, uma vez que a dimensão de uma subálgebra de Cartan é um invariante de $\mathcal{ L}$, e de fato todas as subálgebras de Cartan são conjugadas. Se $\mathcal{ L}$ é simples então $[\mathcal{ H}, \mathcal{ H}]=0$, e $\mathcal{ L}$ admite uma decomposição em subespaços unidimensionais invariantes pela ação de $[H,\bullet]$ para $H\in \mathcal{ H}$:

$$\mathcal{ L}=\mathcal{ H}\oplus \mathcal{ L}_1 \oplus \cdots \oplus \mathcal{ L}_r,$$

dita decomposição de Cartan. Por exemplo, nas álgebras de Lie $\mathcal{ L}= sl_n(k)$ de matrizes $n\times n$ de traço nulo cada matriz $E_{ij}=(\delta{ij})$ com $i\not j$ gera um espaço $\mathcal{ L}_i$ na decomposição de Cartan associada a $\mathcal{ H}$ de matrizes diagonais $H=\begin{pmatrix}\lambda_1&0&\ldots &0\\ 0&\lambda_2&\ldots &0\cr &\cdots &&\\ 0&\ldots &0&\lambda_n\end{pmatrix}$:

$$[H,E_{ij}]=(\lambda_i-\lambda_j)E_{ij}.$$

Em geral uma álgebra de Lie $\mathcal{ L}$ simples admite uma base $\mathcal{ C}=\{ H_i\in \mathcal{ H}, E_i\in \mathcal{ L}_i\}$ na qual para quaisquer $X,Y\in \mathcal{ C}$ vale que [X,Y] pode ser escrito como uma combinação linear inteira de elementos de $\mathcal{ C}$. Bases de $\mathcal{ L}$ com esta propriedade são isoladas para classificar as álgebras simples $\mathcal{ L}$, e são chamadas bases de Chevalley.

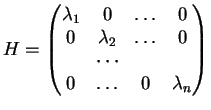Dada uma base de Chevalley $\mathcal{ C}=\{ H_i\in \mathcal{ H}, E_i\in \mathcal{ L}_i\}$ de $\mathcal{ L}$, a ação de ad(E_i) é nilpotente, e pelo visto acima exp(ad(E_i) é um automorfismo de $\mathcal{ L}$. Definimos, para $\alpha\in k$, o automorfismo de $\mathcal{ L}$

$$x_i(\alpha)=exp(\alpha \ ad(E_i)),$$

e consideramos o grupo $\mathcal{ L}(k)$ que estes automorfismos geram em ${\it Aut}_{{\bf AlgLie}_k}( \cal L,\mathcal{ L})$.

No exemplo de sl_n(k) estes automorfismos são exponenciais de matrizes de traço nulo, e estão no grupo de Lie Sl_n(k) associado. Em geral recuperamos em $\mathcal{ L}(k)$ um esqueleto do grupo de Lie.

Com efeito, se dada uma álgebra de Lie simples $\mathcal{ L}$ considerarmos uma base de Chevalley $\mathcal{ C}$ de $\mathcal{ L}$ as relações satisfeitas pelos elementos $x_i(\alpha)$ (que decorrem das constantes estruturais de $\mathcal{ L}$ em termos da base $\mathcal{ C}$, isto é, da expressão dos resultados [H_i,E_j], [E_j,E_l] em termos da base $\mathcal{ C}$) se expressam também em inteiros (e, claro, em $\alpha\in k$). Por exemplo, vale,

$$x_i(\alpha)(E_i)=(E_i),\qquad x_i(\alpha)(H_i)=H_i-2\alpha E_i,$$

e assim por diante.

Isto permite a consideração, em primeiro lugar, de uma ``álgebra de Lie inteira'' $\mathcal{ L}_{\bf Z}$, como sendo o grupo abeliano livre gerado por $\mathcal{ C}$ sobre o qual é definida uma operação [X,Y] com as mesmas constantes estruturais que $\mathcal{ L}$ admitia sobre $\mathcal{ C}$. Se K for agora um corpo qualquer, toma-se o morfismo único $\eta:{\bf Z} \rightarrow K$ sobre $\mathcal{ L}_{\bf Z}$ e assim se define uma álgebra de Lie $\mathcal{ L}_K$ com as constantes estruturais vindas das de $\mathcal{ L}_{\bf Z}$ através de $\eta$. Nesta álgebra é possível definir automorfismos ``vindos'' de $x_1(\alpha)$ da seguinte forma: a matriz que representa $x_i(\alpha)$ tem entradas da forma $l\alpha^j$, onde $l\in {\bf Z}$ é inteiro. Se $a\in K$ então aplicamos nas entradas desta matriz a transformação $l\alpha^j \mapsto \eta(l)a^j$, e isto define um automorfismo x_i(a). O subgrupo de ${\it Aut}_K(\mathcal{ L}_K, \mathcal{ L}_K)$ gerado por tais elementos x_i(a) é denotado por $\mathcal{ L}(K)$. Os elementos $x_i(a)\in \mathcal{ L}(K)$ serão exponenciais, estarão ainda em ``grupos de Lie'', que agora poderão ser tomados sobre qualquer corpo, inclusive sobre corpos finitos.

Não deve ser surpreendente que tomando K um corpo finito recuperamos os grupos clássicos finitos listados em 1. de (I.1). Mais surpreendente são as ``exceções'' que o teorema de classificação de álgebras de Lie simples indica: cinco álgebras, denotadas por G₂, F₄, E₆, E₇ e E₈, que são álgebras de Lie simples não sendo álgebras de Lie de grupos clássicos (o subscrito se refere ao posto da álgebra, isto é, a dimensão de qualquer subálgebra de Cartan). Estas álgebras são ditas excepcionais, e cumprem o mesmo papel dos grupos esporádicos no teorema de classificação de grupos simples. Mas as álgebras esporádicas $\mathcal{ L}$ geram grupos simples finitos $\mathcal{ L}({\bf F}_q)$ ditos grupos de Chevalley (que não são grupos esporádicos).

4. Estruturação livre. As categorias de álgebras aqui consideradas são todas categorias concretas, para cada uma existindo funtores de esquecimento para a categoria Conj. Adjuntos à esquerda de funtores de esquecimento são funtores de estruturação livre.

O funtor de esquecimento

$$\mathcal{ E}_{{\bf Alg}_k}\rightarrow {\bf Conj}$$

tem um adjunto á esquerda que a cada conjunto X, objeto de Conj, associa a álgebra $k\{ X\}$ de polinômios em variáveis não comutativas indexadas por X: como espaço vetorial sobre k é gerado por palavras $x_{i_1}\ldots x_{i_r}$, que se multiplicam por concatenação. O funtor de esquecimento

$$\mathcal{ E}_{{\bf AlgCom}_k}\rightarrow {\bf Conj}$$

da categoria das álgebras comutativas sobre k tem um adjunto á esquerda que a cada conjunto X, objeto de Conj, associa a álgebra mais usual k[ X] de polinômios em variáveis comutativas indexadas por X.

O funtor de esquecimento

$$\mathcal{ E}:{\bf Alg_k}\longrightarrow {\bf Mon}$$

que ignora a estrutura aditiva de uma álgebra e só deixa o monóide resultante, objeto de Mon, tem um adjunto à esquerda que associa a cada monóide M, objeto de Mon, a álgebra do monóide kM, com a multiplicação

$$\mu:m\otimes n\mapsto mn$$

dependendo da operação de M e sendo comutativa exatamente quando M o for. Esta álgebra kM tem estrutura de co-álgebra, co-comutativa sempre, com co-multiplicação e co-unidade dadas por

$$\Delta:m\mapsto m\otimes m,\qquad {\rm e}\qquad \epsilon:m\mapsto 1.$$

Esta co-operações indempendem da operação de M, e como co-álgebra, objeto em ${\bf CoAlg}_k$, kM=kX pode ser definida para qualquer conjunto M=X, objeto em Conj. Caveat emptor: a construção de kX não define adjunto, à esquerda ou à direita, do funtor de esquecimento

$$\mathcal{E}_{{\bf CoAlg}_k}:{\bf CoAlg}_k \longrightarrow {\bf Conj};$$

de fato, ${\bf CoAlg}_k$ tem como objeto final o corpo de constantes k com a estrutura de co-álgebra dada por $1=1\otimes 1$, para cada co-álgebra C, objeto em ${\bf CoAlg}_k$, a co-unidade

$$\epsilon_C:C\longrightarrow k$$

sendo o único morfismo em ${\it Hom}_{{\bf CoAlg}_k} (C,k)$. Como k, depois de esquecida sua álgebra, não é o objeto final de Conj, que é o conjunto com um elemento só, o funtor de esquecimento $\mathcal{E}_{{\bf CoAlg}_k}$ não pode ter adjunto à direita. Por outro lado, o conjunto vazio $\emptyset$, o objeto inicial em Conj, não tem estrutura de co-álgebra, não tendo sequer estrutura de espqço vetorial, e logo o funtor de esquecimento $\mathcal{E}_{{\bf CoAlg}_k}$ não tem adjunto à esquerda. Como espaço vetorial sobre k, objeto em ${\bf Vect}_k$, p espaço vetorial subjacente à co-álgebra kX é dado por

$$kX=\oplus_{x\in X}kx,$$

e $X\rightarrow kX$ é adjunto à esquerda do funtor de esquecimento ${\bf Vect}_k\rightarrow {\bf Conj}$, e assim sequer o funtor de esquecimento ${\bf CoAlg}_k\rightarrow {\bf Vect}_k$ admite adjunto à esquerda.

Se, além de monóide, M=G for um grupo, objeto em Grp, então kG tem um antípoda $S:g\mapsto g^{-1}$ que faz de kG uma álgebra de Hopf (co-comutativa, mas nem sempre comutativa), objeto de ${\bf AlgHopfCocom}_k$.

Se G for finito então o dual ${\it Hom}_k(kG,k)$ é álgebra de Hopf (comutativa, mas nem sempre co-comutativa), objeto de ${\bf AlgHopfCom}_k$, dada pelas funções definidas em G tomando valores em k com a estrutura natural usual de ágebra: ${\it Hom}_k(kG,k)={\it Hom}_{\bf Conj}(G,k)$; a co-multiplicação e a co-unidade são dadas por

$$\Delta(f)(g,h)=f(gh)\qquad {\rm e}\qquad \epsilon(f)=f(1).$$

Se G for, além de finito, comutativo, então esta álgebra de Hopf ${\it Hom}_k(kG,k)$ é isomorfa a $k\hat{G}$, onde $\hat{G}$ é o grupo de caracteres de G (o dual de Pontryagin), o isomorfismo sendo dado pela transformada de Fourier. Se G não for comutativo então kG pode funcionar como funções ${\it Hom}_k (?,k)$ em um espaço ``quântico'' não comutativo inexistente, que generaliza $\hat{G}$ (neste caso, $\hat{G}$, definido como classes de equivalência de módulos simples, -- não mais unidimensionais -- não é mais um grupo).