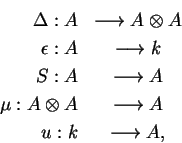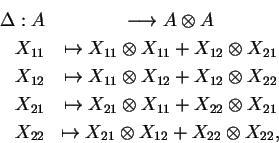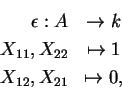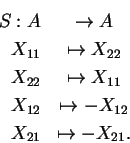Next: Álgebras de Lie e
Up: Bons Antecedentes Algébricos
Previous: A Geometria dos Grupos
Um algebrista, admirando grupos clássicos,
fica fascinado como suas definições independem
grandemente do corpo (ou anel) de constantes k
(no caso de grupos unitários é necessário
um automorfismo involutivo em k, mas isto é
tudo). Mais ainda, grupos clássicos definidos
sobre anéis comutativos
A e A' podem ser comparados
através de um morfismo
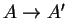 ,
que
define um morfismo dos grupos clássicos por
``mudança de base''. Na verdade, o que o fascina
é o fato de grupos clássicos serem
funtores. Assim, por exemplo, Gln(A)
é o funtor da categoria de anéis comutativos
para a categoria de grupos
,
que
define um morfismo dos grupos clássicos por
``mudança de base''. Na verdade, o que o fascina
é o fato de grupos clássicos serem
funtores. Assim, por exemplo, Gln(A)
é o funtor da categoria de anéis comutativos
para a categoria de grupos
que a cada anel A associa Gln(A).
A aplicação determinante aparece agora como
uma transformação natural
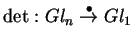 ;
a naturalidade de
;
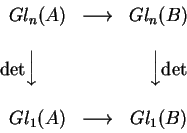
a naturalidade de 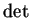 se expressa
na comutatividade do diagrama
se expressa
na comutatividade do diagrama
que resulta da expressão polinomial do
determinante nas coordenadas-entradas das matrizes:
um morfismo de anel nestas entradas forçosamente
preserva esta expressão polinomial, e o diagrama
então comuta.
O núcleo de 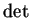 é, como esperado, o
funtor Sln, que associa a cada anel A o
grupo Sln(A). Assumindo que o anel A
é comutativo e contem
o corpo k, ou seja, considerando os funtores
definidos na categoria
é, como esperado, o
funtor Sln, que associa a cada anel A o
grupo Sln(A). Assumindo que o anel A
é comutativo e contem
o corpo k, ou seja, considerando os funtores
definidos na categoria
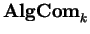 de álgebras
comutativas sobre k, algo ainda mais interessante
acontece: existe um elemento universal para estes
funtores ou, equivalentemente, Sln é
representável: para cada álgebra comutativa
sobre k vale
de álgebras
comutativas sobre k, algo ainda mais interessante
acontece: existe um elemento universal para estes
funtores ou, equivalentemente, Sln é
representável: para cada álgebra comutativa
sobre k vale
Isto significa: o funtor Sln é representado
pela álgebra
![$k[\{X_{ij}\}]/(1-\det(X_{ij}))$](img933.gif) .
Em última análise o que se usa é a
propriedade universal de anéis de polinômios.
Por exemplo,
.
Em última análise o que se usa é a
propriedade universal de anéis de polinômios.
Por exemplo,
Também Gln é representável na categoria
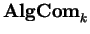 :
neste caso é adicionada
uma variável extra T ao conjunto
:
neste caso é adicionada
uma variável extra T ao conjunto
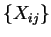 de variáveis, e vale
de variáveis, e vale
Também as condições que definem os outros
grupos clássicos podem ser expressas funtorialmente:
os grupos ortogonais, por exemplo, são grupos
dados por matrizes A que satisfazem AAt=I,
que é uma condição polinomial nas entradas
de A.
O fato de grupos clássicos serem
dados por funtores representáveis se traduz
dizendo que estes objetos que os representam são
co-objetos de Hopf da categoria
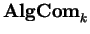 (ver (A.6)).
A categoria
(ver (A.6)).
A categoria
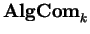 é completa
e cocompleta,
o co-produto de A e B sendo
dado pelo produto tensorial
é completa
e cocompleta,
o co-produto de A e B sendo
dado pelo produto tensorial
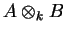 .
Um co-objeto de Hopf
é uma álgebra A,
comutativa sobre k, para a qual existem os morfismos
em
.
Um co-objeto de Hopf
é uma álgebra A,
comutativa sobre k, para a qual existem os morfismos
em
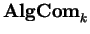 dados por
dados por
dito co-multiplicação,
dito co-unidade ou aumentação,
e
dito antípoda. Estes
dados estão submetidos
aos axiomas que se resumem na comutatividade dos
diagramas
que garante a associatividade do grupo
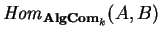 ,
,
que garante que a co-unidade
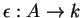 é o morfismo dual
da ``escolha de unidade''
é o morfismo dual
da ``escolha de unidade''
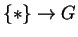 em um grupo G, e
em um grupo G, e
que garante que o morfismo antípoda
funcione como o dual da inversão no grupo.
Uma álgebra comutativa sobre k, objeto
de
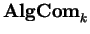 ,
dotada de morfismos
,
dotada de morfismos
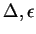 e S que funcionam,
respectivamente, como co-multiplicação,
co-unidade e antípoda (e logo tornam
comutativos os diagramas acima), é dita
uma álgebra de Hopf comutativa
sobre k.
e S que funcionam,
respectivamente, como co-multiplicação,
co-unidade e antípoda (e logo tornam
comutativos os diagramas acima), é dita
uma álgebra de Hopf comutativa
sobre k.
O lema de Yoneda (A.2) garante que
funtores representáveis
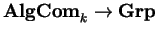 (como os grupos
clássicos) correspondem a álgebras de
Hopf comutativas sobre k. São,
também, os
co-objetos de Hopf de
(como os grupos
clássicos) correspondem a álgebras de
Hopf comutativas sobre k. São,
também, os
co-objetos de Hopf de
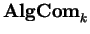 .
.
Funtores representáveis formam naturalmente
uma categoria, em que morfismos são dados
quer por transformações naturais quer
(via o lema de Yoneda), por morfismos em
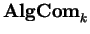 das álgebras de Hopf
comutativas sobre k correspondentes.
Álgebras de Hopf comutativas sobre k
formam naturalmente
uma categoria
das álgebras de Hopf
comutativas sobre k correspondentes.
Álgebras de Hopf comutativas sobre k
formam naturalmente
uma categoria
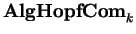 ;
contrariamente
ao caso de álgebras de Lie, uma
álgebra de Hopf é uma álgebra associativa,
e assim existe um funtor de esquecimento
;
contrariamente
ao caso de álgebras de Lie, uma
álgebra de Hopf é uma álgebra associativa,
e assim existe um funtor de esquecimento
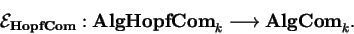 |
(I.3.1) |
Uma álgebra A, objeto de
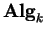 ,
pode ser vista como um espaço vetorial
dotado de morfismos
,
pode ser vista como um espaço vetorial
dotado de morfismos
que fornecem, respectivamente, a
multiplicação e a estrutura de álgebra
sobre k. Estes morfismos devem satisfazer
as condições usuais, que podem
ser expressas por comutatividade de
diagramas apropriados. No caso de uma
álgebra de Hopf sobre k temos morfismos
que satisfazem propriedades duais. A subcategoria
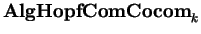 de álgebras de Hopf comutativas e
cocomutativas admite assim um processo
de dualização natural
de álgebras de Hopf comutativas e
cocomutativas admite assim um processo
de dualização natural
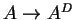 ,
em que a co-multiplicação de AD
é o morfismo dual da multiplicação em A,
a co-unidade é o dual da estruturação
sobre k, e assim por diante.
,
em que a co-multiplicação de AD
é o morfismo dual da multiplicação em A,
a co-unidade é o dual da estruturação
sobre k, e assim por diante.
Exemplos e Exercícios
1. O caso de Sl2. O grupo
clássico Sl2, visto como funtor
representável, é representado
pela álgebra de Hopf comutativa
(o co-objeto de Hopf):
A=k[X11,X12,X21,X22]
/(1-(X11X22-X12X21)).
A co-multiplicação é dada por
a co-unidade por
e o antípoda por
Referências.
O uso de álgebras de Hopf comutativas
em Geometria Algébrica é exposto de
forma clara e elegante em [Wa].




Next: Álgebras de Lie e
Up: Bons Antecedentes Algébricos
Previous: A Geometria dos Grupos
Nicolau C. Saldanha
1999-08-10
![]() é, como esperado, o
funtor Sln, que associa a cada anel A o
grupo Sln(A). Assumindo que o anel A
é comutativo e contem
o corpo k, ou seja, considerando os funtores
definidos na categoria
é, como esperado, o
funtor Sln, que associa a cada anel A o
grupo Sln(A). Assumindo que o anel A
é comutativo e contem
o corpo k, ou seja, considerando os funtores
definidos na categoria
![]() de álgebras
comutativas sobre k, algo ainda mais interessante
acontece: existe um elemento universal para estes
funtores ou, equivalentemente, Sln é
representável: para cada álgebra comutativa
sobre k vale
de álgebras
comutativas sobre k, algo ainda mais interessante
acontece: existe um elemento universal para estes
funtores ou, equivalentemente, Sln é
representável: para cada álgebra comutativa
sobre k vale
![]() (ver (A.6)).
A categoria
(ver (A.6)).
A categoria
![]() é completa
e cocompleta,
o co-produto de A e B sendo
dado pelo produto tensorial
é completa
e cocompleta,
o co-produto de A e B sendo
dado pelo produto tensorial
![]() .
Um co-objeto de Hopf
é uma álgebra A,
comutativa sobre k, para a qual existem os morfismos
em
.
Um co-objeto de Hopf
é uma álgebra A,
comutativa sobre k, para a qual existem os morfismos
em
![]() dados por
dados por
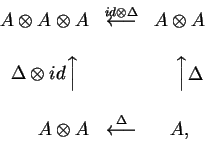
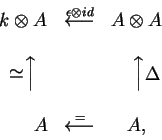
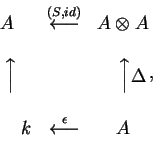
![]() ,
dotada de morfismos
,
dotada de morfismos
![]() e S que funcionam,
respectivamente, como co-multiplicação,
co-unidade e antípoda (e logo tornam
comutativos os diagramas acima), é dita
uma álgebra de Hopf comutativa
sobre k.
e S que funcionam,
respectivamente, como co-multiplicação,
co-unidade e antípoda (e logo tornam
comutativos os diagramas acima), é dita
uma álgebra de Hopf comutativa
sobre k.
![]() (como os grupos
clássicos) correspondem a álgebras de
Hopf comutativas sobre k. São,
também, os
co-objetos de Hopf de
(como os grupos
clássicos) correspondem a álgebras de
Hopf comutativas sobre k. São,
também, os
co-objetos de Hopf de
![]() .
.
![]() das álgebras de Hopf
comutativas sobre k correspondentes.
Álgebras de Hopf comutativas sobre k
formam naturalmente
uma categoria
das álgebras de Hopf
comutativas sobre k correspondentes.
Álgebras de Hopf comutativas sobre k
formam naturalmente
uma categoria
![]() ;
contrariamente
ao caso de álgebras de Lie, uma
álgebra de Hopf é uma álgebra associativa,
e assim existe um funtor de esquecimento
;
contrariamente
ao caso de álgebras de Lie, uma
álgebra de Hopf é uma álgebra associativa,
e assim existe um funtor de esquecimento