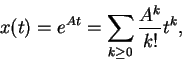Next: A Álgebra dos Grupos
Up: Bons Antecedentes Algébricos
Previous: Grupos Clássicos: Definições
Os grupos clássicos podem ser submetidos à
dissecação por uma variedade de técnicas.
De fato, eles intervêem em quase qualquer área
da matemática. Nesta seção e na próxima
são colocados os pontos de vista com os quais
um geômetra e um algebrista os estudam.
Um geômetra, admirando grupos clássicos,
fica inebriado como estes grupos dependem suavemente
das coordenadas-entradas das matrizes,
e como as operações
algébricas envolvidas, a multiplicação
e a inversão, são operações suaves.
De fato um geômetra, ao ver mencionada a
palavra corpo, só se lembra dos reais e dos
complexos, e então reconhece
estes grupos como variedades diferenciáveis
em que as operações algébricas envolvidas
são suaves. Na verdade o que o fascina é
o fato de grupos clássicos serem objetos da
categoria Diff (ver apêndice B),
de fato objetos de Hopf desta categoria
(ver (A.6)). A denominação consagrada
é, claro, indicar que grupos clássicos
são grupos de Lie.
Rastreando definições, um grupo de
Lie é um grupo, objeto de Grp, que
é uma variedade diferenciável, objeto de
Diff, tal que a multiplicação
e a inversão
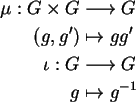
são morfismos em Diff.
Muita coisa é necessária para tornar esta
definição possível: em primeiro lugar,
o produto cartesiano, que é o produto
categórico em Conj, pode ser dotado de
uma estrutura de produto em Grp (isto é
consequência de ter o funtor de esquecimento
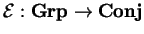 um adjunto à esquerda, dado pela estruturação
livre; ver (A.4)), e também pode ser
dotado de uma estrutura de produto em Diff.
Isto permite que o morfismo em Grp dado pela
multiplicação
um adjunto à esquerda, dado pela estruturação
livre; ver (A.4)), e também pode ser
dotado de uma estrutura de produto em Diff.
Isto permite que o morfismo em Grp dado pela
multiplicação
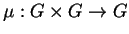 seja morfismo em Diff.
A aplicação do funtor derivada
seja morfismo em Diff.
A aplicação do funtor derivada
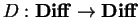 ao morfismo
ao morfismo 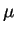 resulta
num morfismo em Diff
resulta
num morfismo em Diff
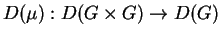 ;
em
particular, derivando na origem
;
em
particular, derivando na origem
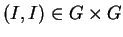 resulta numa aplicação linear entre os
espaços tangentes ((B.5))
resulta numa aplicação linear entre os
espaços tangentes ((B.5))
Uma álgebra de Lie
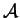 sobre um corpo k
é um espaço vetorial sobre k dotado
de uma operação bilinear
sobre um corpo k
é um espaço vetorial sobre k dotado
de uma operação bilinear
que satisfaz [a,a]=0 para qualquer 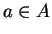 e a identidade de Jacobi
e a identidade de Jacobi
|
[[a,b],c]+
[[b,c],a]+[[c,a],b]=0.
|
(1.2.1) |
Dado um grupo de Lie G, a
estrutura de grupo em
G dota o espaço tangente na identidade
D(G)I da estrutura de uma álgebra de Lie
(ver (B.5)). Esta estruturação se
manifesta de várias maneiras:
por exemplo, derivando o morfismo 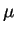 de multiplicação. Para calcular esta
derivada na identidade
de multiplicação. Para calcular esta
derivada na identidade 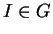 toma-se
uma parametrização local (U,V,h) onde
U é aberto em
toma-se
uma parametrização local (U,V,h) onde
U é aberto em 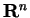 ;
sem perda de
generalidade pode ser exigido
;
sem perda de
generalidade pode ser exigido 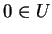 com
h(0)=I, a identidade em G.
Então
com
h(0)=I, a identidade em G.
Então
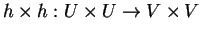 é parametrização local de
é parametrização local de
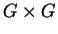 em torno da identidade (I,I)
de
em torno da identidade (I,I)
de 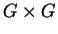 .
A parametrização faz recair o cálculo
da derivada de
.
A parametrização faz recair o cálculo
da derivada de 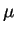 em (I,I) no cálculo da
derivada de
em (I,I) no cálculo da
derivada de
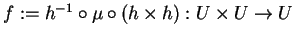 ,
onde
,
onde
é definido em uma vizinhança apropriada
de (0,0).
Expandindo a série de Taylor
de f em torno de (0,0),
e usando
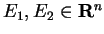 ,
resulta em
,
resulta em
onde
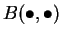 é uma aplicação
bilinear e as reticências indicam termos de ordem
superior. Com esta forma bilinear define-se
é uma aplicação
bilinear e as reticências indicam termos de ordem
superior. Com esta forma bilinear define-se
[E1,E2]=B(E1,E2)-B(E2,E1).
A associatividade de 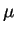 implica
f(f(E1,E2),
E3)=f(E1,f(E2,E3)), que levada à série
de Taylor implica
implica
f(f(E1,E2),
E3)=f(E1,f(E2,E3)), que levada à série
de Taylor implica
B(B(E1,E2),E3)=B(E1,B(E2,E3)).
Daí segue que
![\begin{align}[[E_1&,E_2],E_3]=\notag\\
&B(B(E_1,E_2)E_3)-B(E_3,
B(E_1,E_2))+B(E_3,B(E_2,E_1))-B(B(E_2,E_1),E_3).\notag
\end{align}](img874.gif)
Somando as equações correspondentes para os
termos
[[E2,E3],E1] e
[[E3,E1],E2]
há cancelamento completo de todos os termos
à direita, e logo é satisfeita a
identidade de Jacobi
[[E1,E2],E3]+[[E2,E3],E1]+
[[E3,E1],E2]=0.
Assim, identificando Ei com o vetor tangente
de
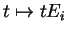 ,
o espaço tangente D(G)I de um grupo
de Lie na identidade tem a estrutura de uma
álgebra de Lie. Esta estrutura se manifestará
sempre que a estrutura diferencial (do grupo
como objeto de Diff) e algébrica (dele
como objeto de Grp) forem usadas em conjunto.
Por exemplo, para qualquer variedade diferenciável
M,
objeto de Diff, o espaço de campos vetoriais
(ou, equivalentemente, de derivações da
álgebra
,
o espaço tangente D(G)I de um grupo
de Lie na identidade tem a estrutura de uma
álgebra de Lie. Esta estrutura se manifestará
sempre que a estrutura diferencial (do grupo
como objeto de Diff) e algébrica (dele
como objeto de Grp) forem usadas em conjunto.
Por exemplo, para qualquer variedade diferenciável
M,
objeto de Diff, o espaço de campos vetoriais
(ou, equivalentemente, de derivações da
álgebra
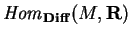 ;
ver (B.5)),
;
ver (B.5)),
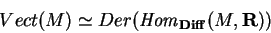 |
(1.2.2) |
tem naturalmente
a estrutura de uma álgebra de Lie
(em geral de dimensão infinita). Esta estrutura,
presente em qualquer variedade diferenciável,
não é a estrutura relevante se M=G
for um grupo de Lie: neste caso observa-se que
G age em Vect(G) da seguinte maneira.
A multiplicação à esquerda
é isomorfismo em Diff (não sendo sequer
morfismo em Grp), e se
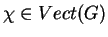 então
então
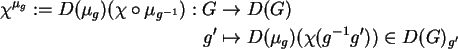
é um campo vetorial em Vect(G). Isto define
uma ação de G em Vect(G), e
um campo
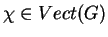 é dito invariante
à esquerda se
é dito invariante
à esquerda se
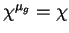 .
O subconjunto GVect(G) de campos
invariantes à esquerda é uma sub-álgebra de
Lie de Vect(G); esta
sub-álgebra GVect(G) é
isomorfa à álgebra de Lie de G definida como
o espaço tangente na identidade D(G)I com
a operação definida como acima, através do
isomorfismo
.
O subconjunto GVect(G) de campos
invariantes à esquerda é uma sub-álgebra de
Lie de Vect(G); esta
sub-álgebra GVect(G) é
isomorfa à álgebra de Lie de G definida como
o espaço tangente na identidade D(G)I com
a operação definida como acima, através do
isomorfismo
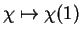 .
Visto na
encarnação de derivações (1.2.2),
um campo
.
Visto na
encarnação de derivações (1.2.2),
um campo 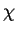 encarado como uma derivação
de
encarado como uma derivação
de
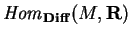 é invariante à esquerda se comutar com a
transformação linear
é invariante à esquerda se comutar com a
transformação linear
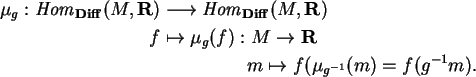
Além destas duas aparições da álgebra de
Lie de um grupo de Lie G, é necessário ao que
segue considerar ainda uma terceira, obtida
através
da ação de G dada por conjugação:
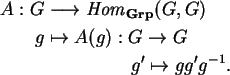
O morfismo A(g)
é isomorfismo em Grp e em
Diff, sendo composta de translações
à direita e à esquerda. Considerando-o como
isomorfismo em Diff podemos tomar sua
derivada na identidade I de G: esta derivada
se denota por
e
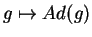 define uma ação de G
em
define uma ação de G
em
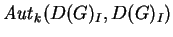 (isto é,
automorfismos de D(G)I como espaço vetorial
sobre k). Como
(isto é,
automorfismos de D(G)I como espaço vetorial
sobre k). Como
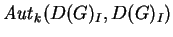 tem
uma estrutura de grupo de Lie (ver exemplo 1.
abaixo), é possível tomar a derivada de
tem
uma estrutura de grupo de Lie (ver exemplo 1.
abaixo), é possível tomar a derivada de
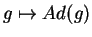 na identidade I,
obtendo uma aplicação de D(G)I no espaço
tangente de
na identidade I,
obtendo uma aplicação de D(G)I no espaço
tangente de
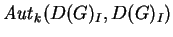 em sua
identidade
em sua
identidade
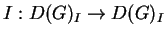 .
Como
.
Como
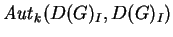 (sendo imagem inversa
do aberto
(sendo imagem inversa
do aberto
 pela função
contínua
pela função
contínua  )
é aberto em
)
é aberto em
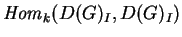 ,
este espaço tangente
é simplesmente
,
este espaço tangente
é simplesmente
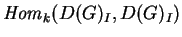 ,
e a
derivada D(Ad)I define uma ação de
álgebras de Lie, denotada por
,
e a
derivada D(Ad)I define uma ação de
álgebras de Lie, denotada por
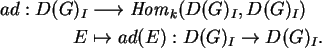
A operação
![\begin{align}D(G)_I\times D(G)_I&\longrightarrow
D(G)_Inotag\\
(E,E')&\mapsto [E,E']:= ad(E)(E')\notag
\end{align}](img894.gif)
é uma (terceira) forma de dotar D(G)I de uma
estrutura de álgebra de Lie. Assim, com um
embarras de richesses, foi indicado o
Teorema de Estruturação do Espaço
Tangente na Identidade como álgebra de Lie.
Se G for um grupo de Lie então o espaço
tangente D(G)I na identidade tem naturalmente a
estrutura de uma álgebra de Lie.
O que falta para ser visto da prova do teorema
depende de como se interprete a palavra
``naturalmente''. As três maneiras de definir
esta estrutura devem servir como uma justificativa
da qualificação ``natural'', mas então
deve ser provado que estas três maneiras coincidem;
isto não é difícil: a representação
adjunta
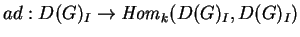 ,
que foi a última forma de apresentar
a estrutura, é calculada pela série de Taylor,
como na primeira definição. Em cada uma das
formas de apresentar foram omitidos detalhes (como
a prova da identidade de Jacobi), que são
rotineiros.
,
que foi a última forma de apresentar
a estrutura, é calculada pela série de Taylor,
como na primeira definição. Em cada uma das
formas de apresentar foram omitidos detalhes (como
a prova da identidade de Jacobi), que são
rotineiros.
O Teorema acima define um funtor da categoria
de GrpLie de grupos de Lie para a categoria
AlgLie de álgebras de Lie:
Exemplos e Exercícios
1. A álgebra de Lie de
 .
O grupo de Lie
.
O grupo de Lie
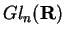 é o grupo de
transformações lineares inversíveis
de
é o grupo de
transformações lineares inversíveis
de 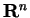 ;
o cálculo que se segue se
aplica para o grupo de transformações lineares
de qualquer espaço vetorial V de dimensão
finita sobre k.
;
o cálculo que se segue se
aplica para o grupo de transformações lineares
de qualquer espaço vetorial V de dimensão
finita sobre k.
Para tomar uma parametrização local em torno
da identidade
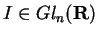 satisfazendo as
condições descritas acima basta fazer
satisfazendo as
condições descritas acima basta fazer
com (cij) matriz 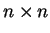 tomada em uma
vizinhança apropriada U da origem em
tomada em uma
vizinhança apropriada U da origem em
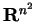 .
A expansão de Taylor de
.
A expansão de Taylor de
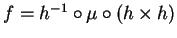 é então simplesmente
é então simplesmente
f(A,B)=A+B+(AB-BA),
onde A,B estão
no espaço
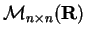 de matrizes
de matrizes 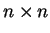 com coeficientes
reais. Assim, a álgebra de Lie de
com coeficientes
reais. Assim, a álgebra de Lie de
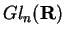 é o espaço
é o espaço
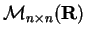 com a operação dada por
[A,B]=AB-BA.
Esta álgebra é denotada por
com a operação dada por
[A,B]=AB-BA.
Esta álgebra é denotada por
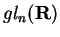 .
.
2. O caso de
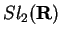 . Um cálculo
análogo pode ser feito para
. Um cálculo
análogo pode ser feito para
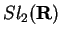 tomando a parametrização em torno de
tomando a parametrização em torno de
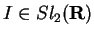 dada por
dada por
onde a entrada d é obtida implicitamente.
De fato, vale
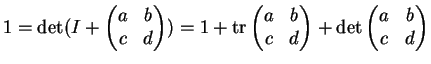 ,
e
a condição para o determinante
ser 1 requer
,
e
a condição para o determinante
ser 1 requer
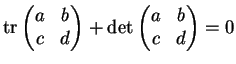 .
Pelo teorema da função
implícita esta condição define
implicitamente d como função suave
perto da origem.
.
Pelo teorema da função
implícita esta condição define
implicitamente d como função suave
perto da origem.
A álgebra de Lie de
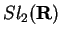 é
dada pela subálgebra de
é
dada pela subálgebra de
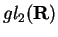 dada pelas matrizes de traço nulo,
como segue de uma aplicação da
aplicação exponencial abaixo. Ela é
denotada por
dada pelas matrizes de traço nulo,
como segue de uma aplicação da
aplicação exponencial abaixo. Ela é
denotada por
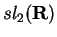 .
.
3. A aplicação exponencial.
Dado um vetor tangente
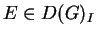 na
álgebra de Lie
na
álgebra de Lie
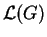 de um grupo
de Lie G, pelo teorema de existência e
unicidade de equações diferenciais
ordinárias existe uma caminho
de um grupo
de Lie G, pelo teorema de existência e
unicidade de equações diferenciais
ordinárias existe uma caminho
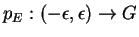 tendo E como vetor
tangente. A associação
tendo E como vetor
tangente. A associação
define a aplicação exponencial
A aplicação exponencial é uma
transformação natural
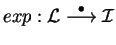 ,
onde
,
onde
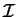 denota o funtor identidade na categoria
de grupos de Lie.
denota o funtor identidade na categoria
de grupos de Lie.
Para
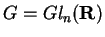 a álgebra de Lie
é o conjunto das matrizes
a álgebra de Lie
é o conjunto das matrizes 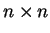 com
[A,B]=AB-BA, como visto em 1..
O sistema
x'(t)=Ax(t) com condição
inicial x(0)=1 tem solução
com
[A,B]=AB-BA, como visto em 1..
O sistema
x'(t)=Ax(t) com condição
inicial x(0)=1 tem solução
e logo a aplicação exponencial neste caso
é a exponencial usual
exp(A)=eA.
Se G é um grupo de Lie e H um subgrupo conexo
(ou, pelo menos, com um número de componentes
conexas enumerável) então
Se
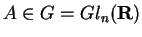 é tal que
A=MJM-1,
onde J é sua forma de Jordan, então
é tal que
A=MJM-1,
onde J é sua forma de Jordan, então
e logo
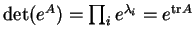 .
Pelo cálculo da exponencial obtido para
.
Pelo cálculo da exponencial obtido para
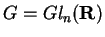 e usando o enunciado acima
com
e usando o enunciado acima
com
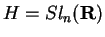 ,
segue que a álgebra de
Lie
,
segue que a álgebra de
Lie
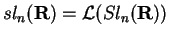 de
de
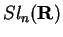 é dada pelas matrizes
é dada pelas matrizes 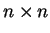 de traço nulo,
conforme anunciado em 2..
de traço nulo,
conforme anunciado em 2..




Next: A Álgebra dos Grupos
Up: Bons Antecedentes Algébricos
Previous: Grupos Clássicos: Definições
Nicolau C. Saldanha
1999-08-10
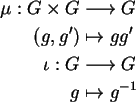
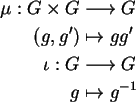
![]() um adjunto à esquerda, dado pela estruturação
livre; ver (A.4)), e também pode ser
dotado de uma estrutura de produto em Diff.
Isto permite que o morfismo em Grp dado pela
multiplicação
um adjunto à esquerda, dado pela estruturação
livre; ver (A.4)), e também pode ser
dotado de uma estrutura de produto em Diff.
Isto permite que o morfismo em Grp dado pela
multiplicação
![]() seja morfismo em Diff.
A aplicação do funtor derivada
seja morfismo em Diff.
A aplicação do funtor derivada
![]() ao morfismo
ao morfismo ![]() resulta
num morfismo em Diff
resulta
num morfismo em Diff
![]() ;
em
particular, derivando na origem
;
em
particular, derivando na origem
![]() resulta numa aplicação linear entre os
espaços tangentes ((B.5))
resulta numa aplicação linear entre os
espaços tangentes ((B.5))
![]() sobre um corpo k
é um espaço vetorial sobre k dotado
de uma operação bilinear
sobre um corpo k
é um espaço vetorial sobre k dotado
de uma operação bilinear
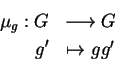
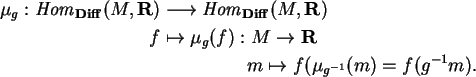
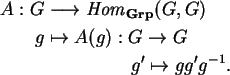
![]() ,
que foi a última forma de apresentar
a estrutura, é calculada pela série de Taylor,
como na primeira definição. Em cada uma das
formas de apresentar foram omitidos detalhes (como
a prova da identidade de Jacobi), que são
rotineiros.
,
que foi a última forma de apresentar
a estrutura, é calculada pela série de Taylor,
como na primeira definição. Em cada uma das
formas de apresentar foram omitidos detalhes (como
a prova da identidade de Jacobi), que são
rotineiros.
![]() .
O grupo de Lie
.
O grupo de Lie
![]() é o grupo de
transformações lineares inversíveis
de
é o grupo de
transformações lineares inversíveis
de ![]() ;
o cálculo que se segue se
aplica para o grupo de transformações lineares
de qualquer espaço vetorial V de dimensão
finita sobre k.
;
o cálculo que se segue se
aplica para o grupo de transformações lineares
de qualquer espaço vetorial V de dimensão
finita sobre k.
![]() satisfazendo as
condições descritas acima basta fazer
satisfazendo as
condições descritas acima basta fazer
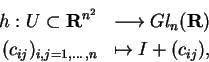
![]() . Um cálculo
análogo pode ser feito para
. Um cálculo
análogo pode ser feito para
![]() tomando a parametrização em torno de
tomando a parametrização em torno de
![]() dada por
dada por
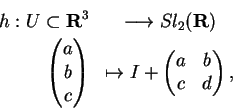
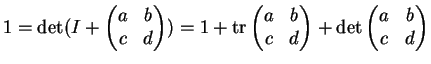 ,
e
a condição para o determinante
ser 1 requer
,
e
a condição para o determinante
ser 1 requer
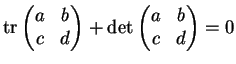 .
Pelo teorema da função
implícita esta condição define
implicitamente d como função suave
perto da origem.
.
Pelo teorema da função
implícita esta condição define
implicitamente d como função suave
perto da origem.
![]() é
dada pela subálgebra de
é
dada pela subálgebra de
![]() dada pelas matrizes de traço nulo,
como segue de uma aplicação da
aplicação exponencial abaixo. Ela é
denotada por
dada pelas matrizes de traço nulo,
como segue de uma aplicação da
aplicação exponencial abaixo. Ela é
denotada por
![]() .
.
![]() na
álgebra de Lie
na
álgebra de Lie
![]() de um grupo
de Lie G, pelo teorema de existência e
unicidade de equações diferenciais
ordinárias existe uma caminho
de um grupo
de Lie G, pelo teorema de existência e
unicidade de equações diferenciais
ordinárias existe uma caminho
![]() tendo E como vetor
tangente. A associação
tendo E como vetor
tangente. A associação
![]() a álgebra de Lie
é o conjunto das matrizes
a álgebra de Lie
é o conjunto das matrizes ![]() com
[A,B]=AB-BA, como visto em 1..
O sistema
x'(t)=Ax(t) com condição
inicial x(0)=1 tem solução
com
[A,B]=AB-BA, como visto em 1..
O sistema
x'(t)=Ax(t) com condição
inicial x(0)=1 tem solução