O caso periódico

Vamos agora explicitar uma solução para a equação $\dot{M} = [M,C]$. A técnica a seguir foi desenvolvida por Adler e van Moerbeke [AM], e é uma área de pesquisa intensa. Apesar da analogia formal entre as equações nos dois casos, existe uma diferença substancial: C não é $\Pi_{anti}M$, porque as posições nos cantos têm sinais trocados. Isso leva a procurar um outro grupo G para o qual uma fatoração conveniente esteja relacionada a esta nova equação. Considere o grupo de laços, ${{\cal{L}}G}= {\cal{L}}GL(n,{\mathbb{C} })$, consistindo de funções suaves $f:{\mathbb{S} }^1 \to GL(n,{\mathbb{C} })$do círculo unitário para as matrizes inversíveis complexas, com multiplicação definida ponto a ponto. A série de Fourier de uma função assim é da forma

$$f(z) = \ldots + \frac{f_{-2}}{z^2} + \frac{f_{-1}}{z} + a_0 + f_1 z + f_2 z^2 + \ldots,$$

onde os coeficientes a_n são matrizes decaindo rapidamente quando $\vert n\vert \to \infty$. O grupo ortogonal e o grupo de matrizes triangulares superiores são substituídos pelo subgrupo ${{\cal{L}}U}$ de laços $f:{\mathbb{S} }^1 \to U(n,{\mathbb{C} })$ tomando valores sobre matrizes unitárias, e o subgrupo ${{\cal{L^+}}G}$ dos laços que admitem continuação analítica para o interior do disco unitário consistindo de matrizes inversíveis e que sejam triangulares superiores com diagonal positiva em z=0.

Para começar, não é claro, mas é verdade, que ${{\cal{L}}G}= {{\cal{L}}U}\ {{\cal{L^+}}G}$. O resultado que faz o papel da ortogonalização de Gram-Schmidt nesse caso pode ser encontrado em [PS] (e continua sendo Gram-Schmidt no contexto adequado). O resultado é mais estrito: os dois termos da fatoração dependem suavemente do laço inicial, e herdam a mesma suavidade -- em particular, suas séries de Fourier decaem com a mesma intensidade. A demonstração de unicidade com as exigências de normalização feitas acima é um pouco diferente da habitual: vamos a ela. Suponha que o laço L(z) admita duas fatorações desse tipo,

L(z) = U(z)R(z) = V(z) S(z).

Então

$$L^*(z)L(z) = R^*(z)R(z) = S^*(z)S(z), \quad z\in {\mathbb{S} }^1,$$

onde a estrela é a operação matricial habitual, e daí

$$(S^*)^{-1}(z)R^*(z) = S(z)R^{-1}(z), \quad z\in{\mathbb{S} }^1, \tag{$\ast$ } \ast$$

na qual o lado direito tem uma continuação analítica (inversível) para o interior do disco unitário, e o lado esquerdo pode ser escrito como

$$(S^*)^{-1}(z)R^*(z) = (S^*)^{-1}({\overline{1/z}})R^*({\overline{1/z}}), \quad z\in {\mathbb{S} }^1.$$

A segunda representação obviamente tem uma continuação analítica para fora do disco unitário, que pode até ser estendida para $z = \infty$. Então os dois lados da equação $(\ast)$descrevem um laço que admite continuação analítica para dentro e fora do círculo unitário, limitada em todo ${\mathbb{C} }$ -- por Liouville,

$$S(z) = C R(z), \quad \vert z\vert \le 1,$$

onde C, uma matriz constante, tem que ser triangular superior com diagonal positiva para z = 0. Assim, todas as fatorações do laço original são da forma

$$L(z) = U(z) C^{-1} C R(z), \quad z\in {\mathbb{S} }^1,$$

para U(z) C^-1 unitária, o que obriga C a ser também unitária -- mais uma vez, não há muitas escolhas: C=I, e fica mostrada a unicidade da fatoração.

Formalmente, a decomposição do grupo induz uma decomposição aditiva na álgebra de Lie associada ${\cal{LG}}$, que consiste de séries

$$a(z) = \ldots + \frac{a_{-2}}{z^2} + \frac{a_{-1}}{z} + a_0 + a_1 z + a_2 z^2 + \ldots$$

sem a exigência de invertibilidade de $a(z), z \in {\mathbb{S} }^1$. A sub-álgebra ${{\cal{L}}U}$ associada ao subgrupo ${{\cal{L}}U}$consiste de elementos da forma

$$\ldots + \frac{a_{-2}}{z^2} + \frac{a_{-1}}{z} + a_0 -a_{-1}^* z - a_{-2}^* z^2 + \ldots,$$

com a₀ anti-hermitiana. A sub-álgebra ${\cal{L}^+}\cal{G}$ de ${{\cal{L^+}}G}$ tem por elementos

$$a_0 + a_1 z + a_2 z^2 + \ldots,$$

onde agora a₀ é triangular superior. É claro que existe uma única decomposição da álgebra ${\cal{LG}}$, dada por

$$a = \Pi_{anti} a +\Pi_{sup} a,$$

onde
$$\begin{align}\Pi_{anti} a &= \ldots + \frac{a_{-2}}{z^2} + \frac{a_{-1}}{z} + (\... ...p} a_0) + (a_1 + a_{-1}^*) z + (a_2 + a_{-2}^*) z^2 + \ldots. \notag \end{align}$$

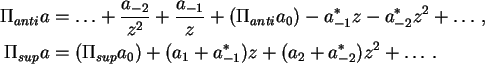
Bom, esse é o grupo de interesse -- resta ver porque. Para começar, interprete a equação original, $\dot{M} = [M,C]$, como um caso especial da família de equações

$$\dot{L}(t,z) = [L(t,z),B(t,z)], \quad z \in {\mathbb{S} }^1,$$

onde

$$L(t,z) = \begin{pmatrix}a_1 & b_1 & 0 & \ldots & z^* b_n \\ ... ...&\ldots&b_{n-1}\\ z b_n & 0 &\ldots&b_{n-1}&a_n \end{pmatrix}$$

e

$$B(t,z) = \begin{pmatrix}0 & -b_1 & 0 & \ldots & z^* b_n\\ b... ...ldots&-b_{n-1}\\ -z^* b_n&0&\ldots&b_{n-1}& 0 \end{pmatrix}.$$

Obviamente, M = M(t) = L(t,1), B = B(t) = B(t,1). O fato surpreendente é que, para resolver essa única equação, vale a pena considerar (e resolver) todas as equações juntas. O acoplamento das equações só aparece no processo de solução: vem das exigências de analiticidade nas decomposições tanto a nível de grupo quanto da álgebra.

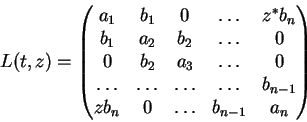
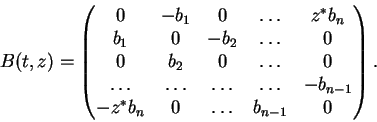
Note que para cada $z \in {\mathbb{S} }^1,$a forma de par de Lax das equações tem por conseqüência a preservação do espectro de L(t,z), quando t varia. Isso faz pensar que obtivemos uma quantidade enorme de leis de conservação para a equação de interesse, mas essas leis são altamente dependentes: o leitor está convidado a estudar o espectro da matriz tridiagonal periódica hermitiana L(0,z)para valores diferentes de $z \in {\mathbb{S} }^1$.

Mais interessante é o fato que as leis de conservação, independentes ou não, ganharam uma interpretação geométrica: as raízes de $p(z,\lambda) = \det(L(t,z) - \lambda I)$não dependem do tempo -- a superfície de Riemann associada a $p(z, \lambda) = 0$ expressa as leis de conservação. Isso não vem ao caso no momento: vamos em vez descrever a solução do látice de Toda periódico por meio da fatoração no grupo de laços.

Teorema: A solução da equação $\dot{L}(t,z) = [L(t,z),B(t,z)],\ \ L(0,z)=L_0(z), z\in{\mathbb{S} }^1,$ é dada por

L(t,z) = [U(t,z)]^* L₀(z) U(t,z),

onde U(t) é obtida pela fatoração

$$\exp(t L_0(z)) = U(t,z) R(t,z),$$

em que $U(t,z) \in {{\cal{L}}U}$ e $R(t,z) \in {{\cal{L^+}}G}$.

Demonstração: Imitando as contas do caso aberto, é só verificar que as fatorações foram bem escolhidas. Derivando as duas evoluções,
$$\begin{align}\dot{L}(t,z) &= [\dot{U}(t,z)]^* L_0 U(t,z) + [U(t,z)]^* L_0 \dot{U... ...t,z)R(t,z) + U(t,z)\dot{R}(t,z), \quad z \in {\mathbb{S} }^1, \notag \end{align}$$
e daí, sempre para $z \in {\mathbb{S} }^1$,
$$\begin{align}\dot{L}(t,z) &= L(t,z) [U(t,z)]^*\dot{U}(t,z) + [\dot{U}(t,z)]^* U(... ...(t,z) &= [U(t,z)]^* \dot{U}(t,z) + \dot{R}(t,z)[R(t,z)]^{-1}. \notag \end{align}$$
Como U(t,z) é unitária, o laço

$$[U(t,z)]^*\dot{U}(t,z)$$

consiste de matrizes anti-hermitianas. Por sua vez, R(t,z) admite uma continuação analítica para o interior do círculo unitário, que na origem é igual a uma matriz triangular superior: o mesmo vale para $\dot{R}(t,z)[R(t,z)]^{-1}$. Assim, a segunda equação descreve a decomposição de L(t,z) numa soma de laços nas sub-álgebras ${{\cal{L}}U}$ e ${\cal{L}^+}\cal{G}$,

$$L(t,z) = \Pi_{anti} L(t,z) + \Pi_{sup} L(t,z),$$

onde

$$\Pi_{anti} L(t,z) = [U(t,z)]^* \dot{U}(t,z), \quad \Pi_{sup} L(t,z) =\dot{R}(t,z)[R(t,z)]^{-1}.$$

Agora, a justificativa de toda a construção: $\Pi_{anti} L(t,z) = B(t,z)$. Logo, mais uma vez, $\dot{L}(t,z) = L(t,z) B(t,z) - B(t,z) L(t,z).$         $\blacksquare$

A partir daqui, muitos caminhos bifurcam. Mais do que no caso aberto, é difícil ver que a construção preserva a forma tridiagonal periódica de L(t,z). E mais uma vez, existe uma interpretação das equações como sistemas integráveis em órbitas coadjuntas (associadas a um grupo de laços). Apesar do espaço ambiente ser de dimensão infinita, as órbitas de interesse são de dimensão finita. A dualidade necessária para identificar o dual da álgebra entretanto requer um certo cuidado técnico [DLT2]. Assim, novamente a invariância temporal da forma do laço admite uma interpretação geométrica, como no caso de dimensão finita, devida essencialmente à forma especial da órbita coadjunta em que se encontra a condição inicial L₀(z). E como no caso de dimensão finita, existe uma família de equações, parametrizada por polinômios, que são resolvidas pela mesma fatoração, e cujos fluxos induzidos comutam entre si.

Uma alternativa para a solução do látice de Toda periódico, historicamente anterior, e igualmente interessante, é devida a Kac e Van Moerbeke [KM]. O laço L(t,z) induz um divisor D(t) na superfície de Riemann mantida fixa pela evolução. A imagem desse divisor pelo mapa de Jacobi descreve uma linha reta na imagem: nesse processo, as variáveis que linearizam a família de fluxos integráveis aparecem naturalmente.