[Date Prev][Date Next][Thread Prev][Thread Next][Date Index][Thread Index]
Re: [obm-l] Matrizes
- To: obm-l@xxxxxxxxxxxxxx
- Subject: Re: [obm-l] Matrizes
- From: "Marcelo Salhab Brogliato" <msbrogli@xxxxxxxxx>
- Date: Thu, 28 Jun 2007 11:20:43 -0300
- DKIM-Signature: a=rsa-sha1; c=relaxed/relaxed; d=gmail.com; s=beta; h=domainkey-signature:received:received:message-id:date:from:to:subject:in-reply-to:mime-version:content-type:references; b=bivvyHufTLNnE0BoXCt12DSp4UK2o80d0OGp++2dMBJze7KQ2knctoJIi6rwW2QwRhm++hnpbY8A/yBdsoc/IhYhZgcvjtoQ1wULgWZQ9J4fMSOfsvLrmAPARB1RS/L9SRQ8x2miJGW6BzHuszfAYms7W8f0Fo9OhT2C1vM0d14=
- DomainKey-Signature: a=rsa-sha1; c=nofws; d=gmail.com; s=beta; h=received:message-id:date:from:to:subject:in-reply-to:mime-version:content-type:references; b=Tbthf6dXnR/57d6M303adslPy7Mq6MePiTGJYhZOrwyuN8YtKcdj4tKgtJj1n4enOhZUDx2C/xDn+nu7WrtVEHkXscd0XmrSeja3zHzH5MTJeweRbRrHi7KYa/WQd8R8zgdHWpFiYjBnfcOiivh3UdcRr3yKOvO4XH9WKKiTI+Y=
- In-Reply-To: <015501c7b979$57195d90$0200000a@METRICAL01>
- References: <015501c7b979$57195d90$0200000a@METRICAL01>
- Reply-To: obm-l@xxxxxxxxxxxxxx
- Sender: owner-obm-l@xxxxxxxxxxxxxx
Olá,
J = (0 -1 ; 1 0) .... S = (a b ; c d) .... JS = (-c -d ; a b)
S^t J S = (0 -ad+bc ; -bc+ad 0) = (0 -1 ; 1 0)
assim:
-ad + bc = -1
-bc + ad = 1 [igual a de cima]
temos que encontrar a,b,c,d tais que: ad - bc = 1
este é um sistema nao linear de 4 variaveis e 1 equacao..
Uma matriz de ordem 2 é simpléticas se, e somente se, é solucao do sistema.
abracos,
Salhab
On 6/28/07, Rejane <rejane@rack.com.br> wrote:
Olá,
aguém poderia me ajudar com essas duas questões?
Seja A uma matriz m x n tal que B = ( AT A ) seja inversível. Prove que C = A B-¹ AT é uma matriz simétrica.
Seja J = 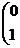
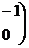 . Diremos que uma matriz de ordem 2 é simplética se ST JS = J. Encontre todas as matrizes reais de ordem 2 que são simpléticas.
. Diremos que uma matriz de ordem 2 é simplética se ST JS = J. Encontre todas as matrizes reais de ordem 2 que são simpléticas.
. Diremos que uma matriz de ordem 2 é simplética se ST JS = J. Encontre todas as matrizes reais de ordem 2 que são simpléticas.