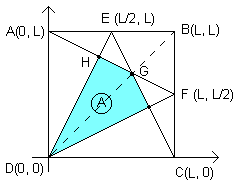
--- Daniel Pini <daniel@fnn.net> escreveu: > Em um quadrado ABCD de área S, os pontos E e F são > médios dos lados AB e BC. O segmento DF se corta com > AE em M; e o segmento CF se corta com o DE em P e > com AE em N. A área do quadrilatero DMNP é ? > R;(no gabarito é 4S/15) Olá Daniel! Na minha resposta os pontos têm uns nomes diferentes dos seus, mas estou mandando uma figura e acho que dá pra entender. Coloque o vértice D no ponto zero dos eixos cartesianos, com os vértices A e C sobre os eixos y e x respectivamente. Chamemos de "L" o lado do quadrado, o que faz com que as coordenadas dos vértices sejam: A(0, L), B(L, L), C(L, 0), D(0, 0) Veja a figura que enviei anexada. Nela você também pode ver os pontos médios E e F com suas coordenadas (L/2, L) e (L, L/2) respectivamente. Como essa figura é simétrica, ao traçarmos BD, esse segmento passará pelo ponto G, e ainda dividirá o quadrilátero cuja área estamos procurando em dois triângulos congruentes. Então se acharmos a área do triângulo DGH, por exemplo, já teremos a área do quadrilátero procurada, que será o dobro da área desse triângulo. A reta BD é a reta y = x (é a reta que passa pelos pontos (0, 0) e (L, L)) e a reta AF é a reta y = -x/2 + L (passa pelos pontos (0, L) e (L, L/2)). E como G é o ponto de intersecção dessas duas retas, temos que igualar o valor de y das duas equações: x = -x/2 + L 3x/2 = L x = 2L/3 Então as coordenadas de G são (2L/3, 2L/3). Agora podemos achar as coordenadas do ponto H com a intersecção das retas AF e DE, cujas equações são respectivamente: y = -x/2 + L y = 2x E podemos achar as coordenadas do ponto H se igualarmos os valores de y das duas equações: -x/2 + L = 2x L = 2x + x/2 5x/2 = L x = 2L/5 Achamos a abcissa de H, agora achamos a ordenada: y = 2x y = 2.2L/5 y = 4L/5 Assim, as coordenadas do ponto H são (2L/5, 4L/5). Agora vemos que se chamarmos a área que queremos de A, podemos escrever que: A/2 = ABD - AGB - AHD Onde ABD, AGB e AHD são as áreas desses 3 triângulos. A área de ABD é metade da área do quadrado ABCD que tem lado L e portanto área igual a L². Para acharmos a área de AGB, chamaremos de base do triângulo o lado AB, que tem medida L. Assim a altura do triângulo será a distância de AB até G. Como a distância de G até o lado CD, que é o eixo x, é de 2L/3 pois este é o valor da sua coordenada y, a distância de G até o lado AB será 1/3 porque a soma dessas duas distâncias tem que dar o tamanho da altura do quadrado, que é L. Agora achamos a área do triângulo de base L e altura L/3: AGB = L.(L/3)/2 AGB = L²/6 Para o triângulo AHD, chamaremos de base o lado AD que tem medida L e nesse caso a altura do triângulo será a distância de H até o lado AD, que é o eixo y, e assim será exatamente o valor da coordenada x do ponto H, que é 2L/5. Agora acharemos a área do triângulo de base L e altura 2L/5: AHD = L.(2L/5)/2 AHD = L²/5 E agora vamos achar o valor de A que é metade da área que temos ao tirar as áreas de AGB e AHD da área ABD: A/2 = ABD - AGB - AHD A/2 = L²/2 - L²/6 - L²/5 A/2 = (15L² - 5L² - 6L²)/30 A/2 = 4L²/30 A/2 = 2L²/15 A = 4L²/15 Mas o problema pediu a área em função da área S do quadrado. Assim, como sabemos que S = L², podemos escrever que: A = 4S/15 Abraços, Rafael. _______________________________________________________________________ Yahoo! Mail Mais espaço, mais segurança e gratuito: caixa postal de 6MB, antivírus, proteção contra spam. http://br.mail.yahoo.com/
areaquadrinotri2.gif