Matrizes de Kasteleyn

Kasteleyn resolveu o problema de contar coberturas por dominós de um retângulo $n \times m$ calculando o determinante de uma matriz. Veremos como usar o determinante de uma matriz K com coeficientes da forma $\pm q^e$, $e \in {\mathbb{Z} }$, para q-contar as coberturas por dominós de uma região: como esta matriz é uma generalização da contruida por Kasteleyn vamos chamá-la de matriz de Kasteleyn.

Lembramos que a matriz de adjacência A de um grafo é uma matriz simétrica com uma linha (e uma coluna) correspondente a cada vértice do grafo. O coeficiente a_ij é igual a 1 se os vértices i e j forem adjacentes e 0 caso contrário. Se o grafo for bipartido, teremos

$$A = \begin{pmatrix}0 & B \\ B^t & 0 \end{pmatrix}$$

desde que listemos primeiro todos os vértices brancos e depois os vértices pretos. Assim, na matriz B, linhas correspondem a vértices brancos e colunas correspondem a vértices pretos e b_ij = 1 se o vértice branco i é vizinho do vértice preto je 0 caso contrário. Na figura abaixo mostramos um exemplo de região quadriculada e seu grafo bipartido correspondente. Neste exemplo

$$B = \begin{pmatrix} 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 &... ...0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 \end{pmatrix}.$$

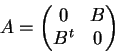
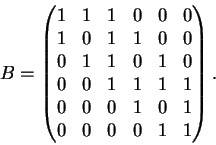
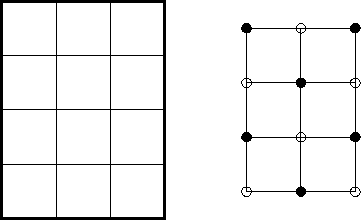
Cada cobertura por arestas do grafo corresponderá a um monômio não nulo na expansão de $\det(B)$; o determinante será portanto o número de coberturas ``pares'' menos o número de coberturas ``ímpares''. Em outras palavras, o número de coberturas por arestas do grafo é o permanente de B; infelizmente o permanente tem muito menos propriedades algébricas interessantes do que o determinante.

No caso de coberturas por dominós, podemos construir a partir de B uma matriz K tal que

$$\det(K) = \sum_T 1.$$

A mágica consiste em fazer com que o sinal do produto dos coeficientes correspondentes a uma cobertura tenha sempre o mesmo sinal que a permutação correspondente, de tal forma que as contribuições ao determinante sempre se somam. Podemos ainda construir uma matriz K_qmultiplicando alguns coeficientes de K por potências de qde tal forma que

$$\det(K_q) = \sum_T q^{h(T)}.$$

Vejamos um exemplo: na figura abaixo indicamos os coeficientes a serem introduzidos na matriz K_qperto de cada aresta. Assim, a entrada i,j de K_q tem o valor indicado na aresta que liga o vértice i branco ao vértice j preto, ou zero se não existir tal aresta (os vértices são numerados na ordem em que se lê). Temos

$$K_q = \begin{pmatrix} 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 0 & -q^{-... ...0 & 1 & 0 & -q^{-3} \\ 0 & 0 & 0 & 0 & 1 & -q^3 \end{pmatrix}$$

e $\det(K) = q^3 + q^2 + 2 q + 3 + 2 q^{-1} + q^{-2} + q^{-3}$.

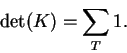
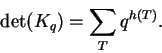
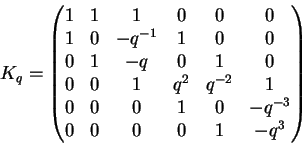
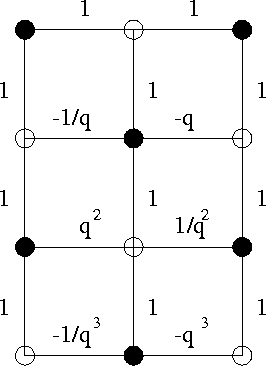
Estes coeficientes podem ser construidos da seguinte forma: tome as arestas de uma cobertura e atribua a elas coeficientes tais que o monômio correspondente traga a contribuição correta ao determinante de K_q. A seguir, tome uma sub-árvore maximal do grafo contendo todas as arestas já consideradas na fase anterior e atribua a todas as novas arestas desta árvore coeficientes arbitrários (por exemplo, sempre 1). Procure agora um quadrado (i.e., uma posição de flip) tal que três das arestas já tenham coeficientes e atribua à aresta restante um coeficiente tal que o produto dos coeficientes sobre as duas arestas correspondentes ao flip positivo seja -q vezes o produto dos coeficientes sobre as outras duas arestas. Repita o processo até que todas as arestam tenham recebido coeficientes.

A construção garante que se uma cobertura traz a contribuição correta a $\det K_q$ então toda cobertura vizinha por um flip também traz a contribuição correta. Observe que a paridade da permutação é invertida a cada flip mas o sinal do produto dos coeficientes das arestas está sendo devidamente compensado. Se a região for simplesmente conexa então todas as coberturas são ligadas por flips, o que demonstra nossa afirmação.

O caso de coberturas por lozangos é análogo, com a diferença que flips não mais invertem a paridade da permutação. Assim, para atribuir coeficientes às arestas que não pertencem à árvore maximal devemos procurar hexágonos tais que cinco das seis arestas já receberam coeficientes e fazer com que o produto dos coeficientes das três arestas correspondentes ao flip positivo seja q vezes o produto dos coeficientes sobre as outras três arestas.