Funções altura e a altura total de uma cobertura

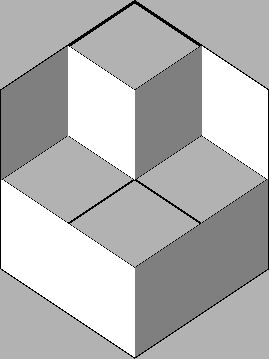
Uma das ferramentas mais simples e poderosas para o estudo de coberturas por dominós ou lozangos são as funções altura. A forma mais simples de apresentar funções altura é provavelmente olhar para uma cobertura por lozangos, talvez pintando os lozangos como abaixo.

Olhando para esta figura, é quase inevitável ver uma pilha de cubos unitários ([DT]). Se as arestas dos cubos forem paralelas aos eixos x, y e z, a figura é obtida projetando ortogonalmente a pilha sobre o plano x+y+z = 0. O valor de x+y+z em um vértice é deduzido portanto não pela posição do vértice no plano e sim pela interpretação da figura como projeção em um plano de um objeto tridimensional. Ou seja, o valor de x+y+z depende da cobertura por lozangos mas x-y, x-z ou y-z não: x+y+z é nossa função altura. 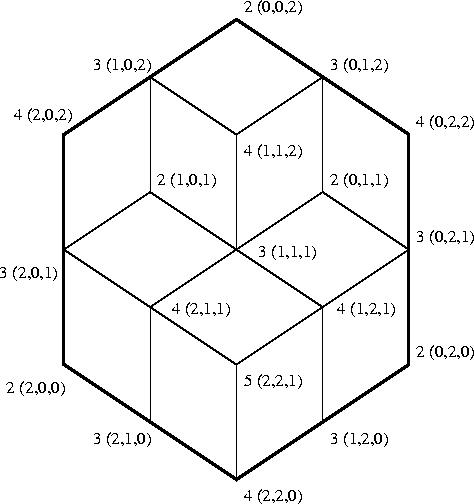Na figura abaixo indicamos o valor da função altura e as coordenadas em ${\mathbb{R} }^3$ dos vértices dos lozangos.

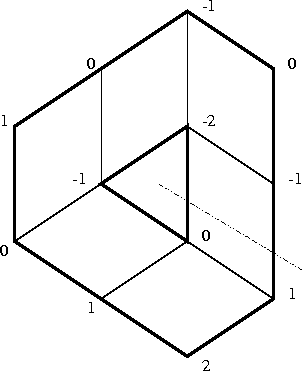
É interessante tornar independente de visualização o processo de obter a função altura de uma cobertura de lozangos. Observemos que bordos de lozangos têm três direções possíveis, correspondentes aos três eixos (em ${\mathbb{R} }^3$). Se andamos sobre um bordo de lozango o valor da coordenada correspondente ao eixo sobe ou desce de 1 e as demais coordenadas permanecem constantes; o valor da função altura x+y+zdeve portanto também subir ou descer de 1 dependendo da direção, conforme indicado pelas setas na figura abaixo. Isto nos permite calcular a diferença entre o valor da função altura em dois pontos: completamos a definição escolhendo um ponto do bordo da região como ponto base e declarando que a função altura neste ponto é zero. Resta demonstrar que a definição acima é consistente, i.e., que o valor da função altura em um dado ponto independe da escolha do caminho ou, equivalentemente, que o aumento no valor da função correspondente a um caminho fechado é sempre zero.

Vemos que as setas orientam os bordos de triângulos equiláteros, no sentido anti-horário para triângulos com vértice para a esquerda e no sentido horário para triângulos com vértice para a direita. Se mantivermos todas as arestas este padrão de setinhas (uma espécie de 1-forma discreta) não pode ser integrado, i.e., não existe uma função tal que o padrão de setinhas descreva a diferença entre o valor da função em pontos vizinhos. Voltando à analogia com formas diferenciais, isto ocorre porque o contorno de um triângulo tem integral 3 ou -3, ou seja, a forma não é exata. Se juntarmos os triângulos dois a dois em uma cobertura por lozangos e eliminarmos as arestas interiores aos lozangos então a integral ao redor de cada lozango passa a ser 0 e a 1-forma passa a ser pelo menos fechada.

Se a região for simplesmente conexa podemos concluir que a 1-forma é exata e integrá-la para obter a função altura. Se a região não for simplesmente conexa, nem sempre podemos definir globalmente uma função altura (da mesma forma que não podemos definir uma função argumento em ${\mathbb{R} }^2 - \{0\}$). Podemos ou introduzir um corte ou definir um conceito de seção altura ([STCR]). Aqui consideraremos apenas regiões simplesmente conexas de modo que não discutiremos estas dificuldades.

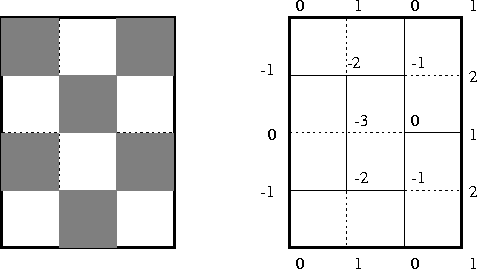
Esta segunda forma de definir a função altura (localmente via diferenças) generaliza-se facilmente para dominós. Pintamos os quadrados de branco e preto; definimos que ao andar pelo bordo de um dominó o valor da função altura aumenta de 1 (resp., diminui de 1) se o quadrado à esquerda do caminho é branco (resp., preto). Em outras palavras, o bordo de quadrados brancos (resp. pretos) é orientado no sentido anti-horário (resp. horário). Como no caso dos lozangos, isto nos permite associar uma função altura a cada cobertura por dominós de uma região simplesmente conexa. A figura abaixo mostra a função altura associada a uma cobertura por dominós.

Funções altura permitem demonstrar que o espaço das coberturas por lozangos ou dominós de regiões simplesmente conexas são conexos via alguns movimentos simples chamados flips ([T], [STCR]). Para dominós, um flip consiste em tomar dois dominós paralelos vizinhos formando um quadrado $2 \times 2$ e girá-los de $90^\circ$; para lozangos um flip consiste em tomar três lozangos vizinhos formando um hexágono regular e girá-los de $60^\circ$. O que há de especial nestes movimentos é que eles alteram o valor da função altura em um único ponto: o centro do quadrado ou hexágono. Flips podem assim ser naturalmente classificados como positivos (quando aumentam o valor da função altura) ou negativos (caso contrário). Podemos definir a altura total de uma cobertura como sendo o número de flips positivos menos o número de flips negativos usados para chagar na cobertura em questão a partir de uma cobertura fixa, chamada de cobertura base. Equivalentemente, podemos calcular a altura total de uma cobertura tomando a função altura para a cobertura, subtraindo daí a função altura para a cobertura base, somando o valor desta diferença sobre todos os vértices de dominó (resp., lozango) e dividindo o total por 4 (resp., 3). Para o caso de coberturas por lozangos, a altura total é simplesmente o número de cubinhos na pilha de cubos correspondente. Denotaremos a altura total de uma cobertura T por h(T).