Coberturas por dominós e por lozangos

Um problema clássico de combinatória é o de contar as coberturas por arestas de um grafo, freqüentemente de um grafo bipartido. Uma cobertura por arestas é um conjunto de arestas do grafo tal que todo vértice é o extremo de exatamente uma aresta do conjunto. Não tentaremos discutir o problema nesta versão geral: estaremos apenas interessados em grafos que, informalmente falando, são localmente como ${\mathbb{Z} }^2$. O grafo ${\mathbb{Z} }^2$ é o grafo infinito cujos vértices são pares (i,j), com $i, j \in {\mathbb{Z} }$, com arestas ligando (i,j) a $(i \pm 1, j)$ e $(i, j \pm 1)$. Não veremos aqui a definição desta classe de grafos; consideraremos apenas uma subclasse já bastante rica, a dos subgrafos (não necessariamente completos) conexos e finitos de ${\mathbb{Z} }^2$. A figura abaixo mostra exemplos de grafos deste tipo.

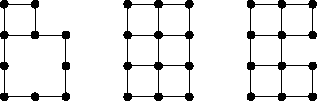
Uma forma útil de desenhar este tipo de grafo é substituir cada vértice por um quadrado unitério. Vértices vizinhos correspondem a quadrados adjacentes; quando dois vértices vizinhos em ${\mathbb{Z} }^2$ pertencem a nosso grafo mas a aresta que os liga não, dizemos que há uma parede entre os quadrados. Assim, um grafo vira uma região quadriculada, possivelmente com paredes internas. Os grafos da figura anterior correspondem às regiões abaixo.

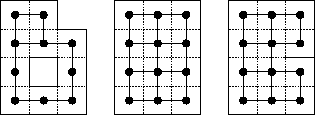
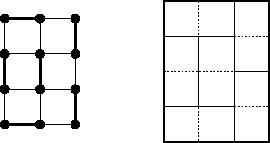
Arestas no grafo podem ser traduzidas como dominós dentro da região correspondente: o dominó cobre os quadrados associados aos vértices da aresta. Daí nossa identificação entre coberturas por arestas e coberturas por dominós: uma cobertura por dominós é simplesmente uma forma de encher uma caixa (a região) com dominós. A figura abaixo mostra uma cobertura por arestas de um grafo e a cobertura por dominós a ele associada.

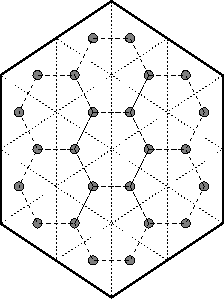
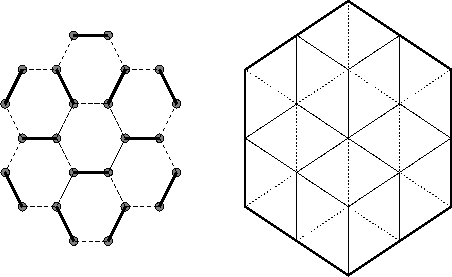
Uma classe de regiões similar é a de regiões formadas por triângulos equiláteros de aresta 1; regiões deste tipo correspondem a subgrafos da ``colméia infinita'' mostrada abaixo. Ao invés de dominós, devemos considerar lozangos de lado 1 e ângulos internos de $\pi/3$ e $2\pi/3$; como antes, coberturas por arestas no grafo correspondem a coberturas por lozangos na região: a figura abaixo mostra um exemplo desta correspondência.

Um dos nossos objetivos neste capítulo é o de mostrar como contar coberturas. Chamando a cobertura típica de T, queremos assim calcular $\sum_T 1$. Na próxima seção atribuiremos a cada cobertura T um índice h(T)que nos permitirá q-contar coberturas, i.e., calcular $\sum_T q^{h(T)}$.