Next: Coberturas por domin�s e Up: Domin�s e q-contagem Previous: N�meros binomiais

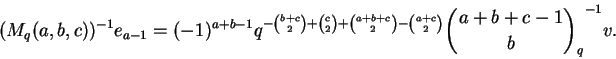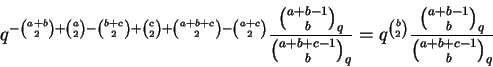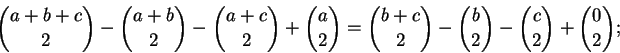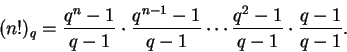
N�meros binomiais e q-contagem

Na se��o anterior supomos que o leitor conhecia a fun��o fatorial. Vamos come�ar esta se��o definindo (n!)_q.

Defini��o 1.7: Seja n um natural; definimos

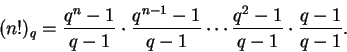
$\begin{displaymath}(n!)_q = \frac{q^n - 1}{q-1} \cdot \frac{q^{n-1} - 1}{q-1} \cdots \frac{q^2 - 1}{q - 1} \cdot \frac{q - 1}{q - 1}. \end{displaymath}$

� claro que podemos tamb�m definir recursivamente (0!)_q = 1,

$\begin{displaymath}(n!)_q = \frac{q^n - 1}{q - 1} ((n-1)!)_q = (q^{n-1} + q^{n-2} + \cdots + q + 1) ((n-1)!)_q. \end{displaymath}$

Vejamos agora uma interpreta��o combinat�ria para estes polin�mios.

Lembramos que n! � o n�mero de permuta��es de $\{1, 2, \ldots, n\}$ . Definimos o n�mero de invers�es $i(\pi)$ de uma permuta��o $\pi$ como sendo o n�mero de pares (i,j) com $1 \le i < j \le n$ tais que $\pi(i) > \pi(j)$ .

Proposi��o 1.8: Seja n um natural; temos

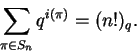
$\begin{displaymath}\sum_{\pi \in S_n} q^{i(\pi)} = (n!)_q. \end{displaymath}$

Ou seja, o polin�mio (n!)_q serve para q-contar as permuta��es $\pi$ com rela��o a este �ndice $i(\pi)$ .

Dem: Usando indu��o, basta mostrar que

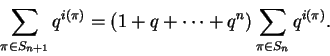
$\begin{displaymath}\sum_{\pi \in S_{n+1}} q^{i(\pi)} = (1 + q + \cdots + q^n) \sum_{\pi \in S_n} q^{i(\pi)}. \end{displaymath}$

Pensando em permuta��es como listas de n�meros, um elemento de S_n+1 � obtido a partir de um elemento de S_ninserindo o n�mero n+1 em alguma posi��o. Se n+1 for inserido no final, n�o criamos nenhuma nova invers�o; se for inserido na pen�ltima posi��o, criamos uma invers�o e finalmente se for inserido no in�cio criamos n invers�es. Em geral, a partir de uma permuta��o com k invers�es criamos n+1permuta��es com $k, k+1, \ldots k+n$ novas invers�es, o que demonstra nossa f�rmula para (n!)_q. $\blacksquare$

Defini��o 1.9: Sejam n e m inteiros. Definimos

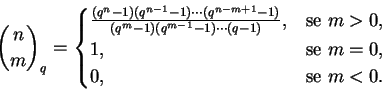
$\begin{displaymath}\binom{n}{m}_q = \begin{cases} \frac{(q^n - 1)(q^{n-1} - 1)\c... ... 0,\\ 1,&\text{se } m = 0,\\ 0,&\text{se } m < 0. \end{cases}\end{displaymath}$

Assim $\binom{n}{m}_q \in {\mathbb{C} }(q)$ fica definido para quaisquer n, m inteiros. Observe que substituindo q por 1 recuperamos os n�meros binomiais. Observe tamb�m que quando n � natural e $0 \le m \le n$ temos

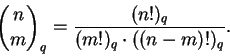
$\begin{displaymath}\binom{n}{m}_q = \frac{(n!)_q}{(m!)_q \cdot ((n-m)!)_q}. \end{displaymath}$

Estas defini��es podem ser estendidas a dom�nios ainda maiores mas isto est� fora de nossos interesses neste cap�tulo.

Proposi��o 1.10: Sejam n e m um inteiros. Temos
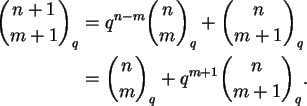
$\begin{align}\binom{n+1}{m+1}_q &= q^{n-m} \binom{n}{m}_q + \binom{n}{m+1}_q \notag\\ &= \binom{n}{m}_q + q^{m+1} \binom{n}{m+1}_q.\notag \end{align}$

Dem: Basta substituir. $\blacksquare$

No caso cl�ssico, vimos que $\binom{x}{m}$ � um polin�mio de grau mna vari�vel x. No nosso caso, podemos fazer uma afirma��o semelhante. Para todo natural m existe um polin�mio $P_m \in {\mathbb{C} }(q)[X]$ de grau m na vari�vel X tal que $\binom{n}{m}_q = P_m(q^n)$ para todo inteiro n. De fato,

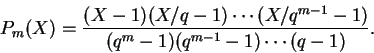
$\begin{displaymath}P_m(X) = \frac{(X - 1)(X/q - 1)\cdots (X/q^{m-1} - 1)}% {(q^m - 1)(q^{m-1} - 1)\cdots (q - 1)}. \end{displaymath}$

Mais geralmente, se $Q \in {\mathbb{C} }(q)[X]$ tem grau menor ou igual a mna vari�vel X ent�o existem $b_0, \ldots, b_n \in {\mathbb{C} }(q)$ tais que

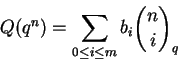
$\begin{displaymath}Q(q^n) = \sum_{0 \le i \le m} b_i \binom{n}{i}_q \end{displaymath}$

para todo inteiro n.

Vejamos agora interpreta��es combinat�rias para $\binom{n}{m}_q$ . Para isso voltemos � interpreta��o de $\binom{n}{m}$ como o n�mero de caminhos ligando v�rtices em um ret�ngulo de lados m e n-m. Para $\binom{n}{m}_q$ , cada caminho contribui com q^a, onde a � a �rea abaixo do caminho. Para um subconjunto de m elementos de $\{1, 2, \ldots n\}$ , portanto, o expoente de q � a soma dos elementos do subconjunto menos $1 + 2 + \cdots + m = m(m+1)/2$ . Assim, o caminho na nossa figura na se��o anterior corresponde a um termo de q²⁴. O leitor pode verificar diretamente, por exemplo, que

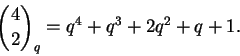
$\begin{displaymath}\binom{4}{2}_q = q^4 + q^3 + 2 q^2 + q + 1. \end{displaymath}$

Um racioc�nio combinat�rio simples nos d� a f�rmula de recorr�ncia, demonstrando que nossa interpreta��o � correta. Seja (provisoriamente) F(a,b) o polin�mio em q definido como acima em um ret�ngulo $a \times b$ . Se a = 0 ou b = 0 temos $F(a,b) = \binom{a+b}{a}_q = 1$ . Se $a, b \ge 1$ , o �ltimo trecho do caminho pode ser vertical ou horizontal. Se for horizontal, retirando este �ltimo trecho temos um caminho de mesma �rea em um ret�ngulo $a \times (b-1)$ . Se for vertical, retirando este �ltimo trecho temos um caminho em um ret�ngulo $(a-1) \times b$ , mas a �rea diminuiu de b. Somando estas contribui��es temos

F(a,b) = F(a,b-1) + q^b F(a-1,b)

o que � equivalente a recorr�ncia da proposi��o 1.10.

Esta interpreta��o � �til para ajudar a ver alguns fatos b�sicos sobre $\binom{n}{m}_q$ . Refletindo o ret�ngulo (e os caminhos) na diagonal x=y temos $\binom{n}{m}_q = \binom{n}{n-m}_q$ . O grau de $\binom{n}{m}_q$ � m(n-m), a �rea total do ret�ngulo; os coeficientes de 1 e de q^m(n-m) s�o ambos iguais a 1, correspondendo aos caminhos no extremo de baixo e de cima. Girando o caminho de meia volta ao redor do centro do ret�ngulo trocamos o valor da �rea de i por m(n-m) - i: isto prova que os coeficientes de qⁱ e de q^{m(n-m) - i}s�o sempre iguais.

Existe uma outra defini��o combinat�ria importante para q-n�meros binomiais usando �lgebra linear sobre corpos finitos.

Proposi��o 1.11: Seja ${\mathbb{F} }_q$ o corpo finito com q elementos (onde q � uma pot�ncia de primo) e seja V um ${\mathbb{F} }_q$ -espa�o vetorial de dimens�o n; V tem exatamente $\binom{n}{m}_q$ subespa�os W de dimens�o m.

Observemos que aqui, pela primeira vez, q deixa de ser uma vari�vel puramente formal e passa a assumir valores inteiros, de tal forma que $\binom{n}{m}_q$ passa tamb�m a assumir valores inteiros. Daremos duas demonstra��es independentes para esta nova interpreta��o combinat�ria de $\binom{n}{m}_q$ : uma por indu��o, usando as f�rmulas de recorr�ncia, e outra relacionando mais diretamente este problema combinat�rio com o primeiro (que fala de caminhos em uma grade).

Dem: A demonstra��o � por indu��o. Chamamos provisoriamente de f(n,m,q)o n�mero de subespa�os de dimens�o m de $V \equiv {\mathbb{F} }_q^n$ . Como s� existe um subespa�o de dimens�o 0 e um subespa�o de dimens�o n, temos f(n,0,q) = f(n,n,q) = 1 para todo $n \ge 0$ . Para calcular f(n+1,m+1,q), consideremos $V_1 = {\mathbb{F} }_q^n \subset V = {\mathbb{F} }_q^{n+1}$ . Seja $W \subset V$ um subespa�o de dimens�o m+1; a dimens�o de $W_1 = W \cap V_1$ pode ser m ou m+1. No primeiro caso temos f(n,m,q) poss�veis W₁e cada um deles precisa ser engordado com um elemento de V - V₁para virar um W: existem qⁿ⁺¹ - qⁿ = qⁿ (q-1) elementos de V - V₁mas cada W � gerado por q^m+1 - q^m = q^m (q-1) destes elementos. Assim, temos q^n-m f(n,m,q) subespa�os Wpara os quais $W \cap V_1$ tem dimens�o m. Por outro lado, temos f(n,m+1,q) subespa�os Wpara os quais esta dimens�o � m+1; somando os dois casos temos

f(n+1,m+1,q) = q^n-m f(n,m,q) + f(n,m+1,q);

como esta recorr�ncia � a mesma que encontramos para $\binom{n}{m}_q$ e as condi��es iniciais tamb�m s�o as mesmas temos $f(n,m,q) = \binom{n}{m}_q$ .

Para a segunda demonstra��o, lembramos que podemos descrever um subespa�o W (de dimens�o m) de Kⁿ (onde K � um corpo) via uma matriz $A \in K^{m \times n}$ de posto m: W � o espa�o gerado pelas linhas de A. Para cada subespa�o W existem muitas matrizes A correspondentes: mais precisamente, duas matrizes A₁ e A₂ definem o mesmo subespa�o Wse e somente se existe uma matriz quadrada invers�vel B com A₁ = B A₂. A forma usual de tomar um representante de cada classe de equival�ncia � considerar matrizes escalonadas por linhas, i.e., para cada $A \in K^{m \times n}$ de posto mexiste uma �nica matriz invers�vel B tal que BA � escalonada por linhas. Lembramos que uma matriz escalonada por linhas � aquela que satisfaz as seguintes condi��es:

o primeiro elemento n�o nulo de cada linha � sempre 1,
em uma coluna onde aparece o primeiro elemento n�o nulo de uma linha todos os outros elementos s�o iguais a 0,
se a linha i₁ est� acima da linha i₂, o primeiro elemento n�o nulo da linha i₁aparece antes do primeiro elemento n�o nulo da linha i₂.

Um exemplo talvez torne mais claro o significado destas condi��es; a matriz

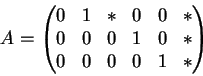
$\begin{displaymath}A = \begin{pmatrix} 0 & 1 & \ast & 0 & 0 & \ast \\ 0 & 0 & 0 & 1 & 0 & \ast \\ 0 & 0 & 0 & 0 & 1 & \ast \end{pmatrix} \end{displaymath}$

� escalonada por linhas, onde os $\ast$ 's indicam posi��es que podem ser preenchidas com qualquer elemento de K. Chamemos de tipo de W (ou de A) ao conjunto dos �ndices (j) das colunas onde aparece o primeiro elemento n�o nulo de alguma linha: o exemplo acima tem tipo $\{2,4,5\}$ ; mais precisamente, variando o valor dos $\ast$ 's temos todas as matrizes A de tipo $\{2,4,5\}$ . Os tipos poss�veis s�o os subespa�os de m elementos de $\{1, 2, \ldots n\}$ , que equivalem aos caminhos em um ret�ngulo de m linhas e n-m colunas: este caminho � obtido a partir da matriz jogando fora as colunas onde aparece o primeiro elemento n�o nulo de alguma linha (estas colunas s�o obrigatoriamente preenchidas pelos vetores da base can�nica) e separando as posi��es 0 (onde devemos obrigatoriamente escrever 0) das posi��es $\ast$ (onde temos liberdade de escrever qualquer elemento de K). O caminho correspondente � matriz A acima est� indicado a seguir. $\blacksquare$

$\begin{figure}\begin{center} \epsfig{width=3cm,file=q1-2c.eps}\end{center} \end{figure}$

Vejamos agora resultados an�logos aos da primeira se��o.

Proposi��o 1.12: Para quaisquer $n \in {\mathbb{N} }$ , $m, \ell \in {\mathbb{Z} }$ temos

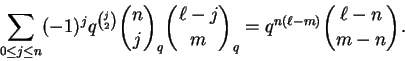
$\begin{displaymath}\sum_{0 \le j \le n} (-1)^j q^{\binom{j}{2}} \binom{n}{j}_q \binom{\ell-j}{m}_q = q^{n(\ell-m)} \binom{\ell-n}{m-n}. \end{displaymath}$

Dem: Por indu��o em n, sendo trivial o caso n = 0. O caso n = 1 � a identidade recursiva da Proposi��o 1.10 (apenas mudando o nome das vari�veis):

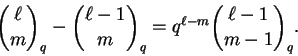
$\begin{displaymath}\binom{\ell}{m}_q - \binom{\ell-1}{m}_q = q^{\ell-m} \binom{\ell-1}{m-1}_q.\end{displaymath}$

Suponha a identidade demonstrada para n; para n+1 temos
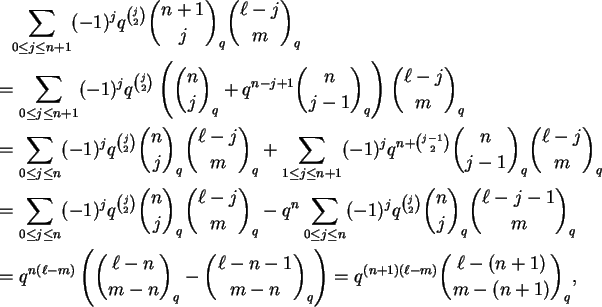
$\begin{align}&\phantom{=} \sum_{0 \le j \le n+1} (-1)^j q^{\binom{j}{2}} \binom{... ..._q}\right) = q^{(n+1)(\ell-m)} \binom{\ell-(n+1)}{m-(n+1)}_q, \notag \end{align}$
o que demonstra a identidade para n+1 e conclui a demonstra��o. $\blacksquare$

Observe a total analogia entre a Proposi��o 1.4 e a Proposi��o 1.12; at� a demonstra��o da proposi��o mais geral � obtida simplesmente inserindo q nos lugares apropriados.

Corol�rio 1.13: Seja n um inteiro positivo e $P \in {\mathbb{C} }(q)[X]$ um polin�mio de grau menor do que n em X. Ent�o

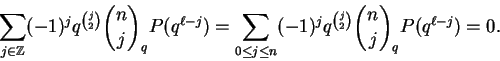
$\begin{displaymath}\sum_{j \in {\mathbb{Z} }} (-1)^j q^{\binom{j}{2}} \binom{n}{... ...n} (-1)^j q^{\binom{j}{2}} \binom{n}{j}_q P(q^{\ell - j}) = 0. \end{displaymath}$

Dem: An�loga � do Corol�rio 1.5, usando a Proposi��o 1.12. $\blacksquare$

Finalmente, a Proposi��o 1.14 abaixo � an�loga � Proposi��o 1.6.

Proposi��o 1.14: Para quaisquer naturais a, b, c temos
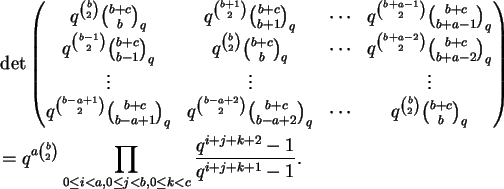
$\begin{align}&\det \begin{pmatrix} q^{\binom{b}{2}} \binom{b+c}{b}_q & q^{\binom... ... \le j < b, 0 \le k < c} \frac{q^{i+j+k+2}-1}{q^{i+j+k+1}-1}. \notag \end{align}$

Novamente o lado direito � invariante por permuta��es de a, b, c, o que n�o � evidente para o lado esquerdo. Por outro lado, o lado esquerdo � claramente um polin�mio em q; o leitor � convidado a tentar demonstrar diretamente que o lado direito � um polin�mio em q.

Usaremos na demonstra��o a equa��o

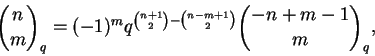
$\begin{displaymath}\binom{n}{m}_q = (-1)^m q^{\binom{n+1}{2} - \binom{n-m+1}{2}} \binom{-n+m-1}{m}_q, \end{displaymath}$

que vem de escrevermos
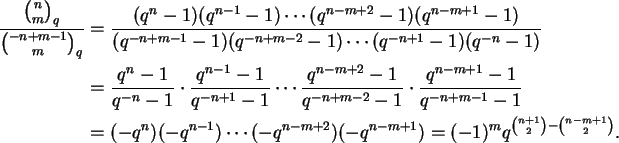
$\begin{align}\frac{\binom{n}{m}_q}{\binom{-n+m-1}{m}_q} &= \frac{(q^n - 1)(q^{n-... ...)(-q^{n-m+1}) = (-1)^m q^{\binom{n+1}{2} - \binom{n-m+1}{2}}. \notag \end{align}$
Como a demonstra��o segue muito de perto a da Proposi��o 1.6 seremos um pouco mais sucintos.

Dem: Seja

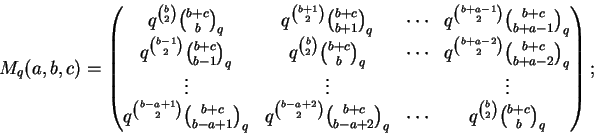
$\begin{displaymath}M_q(a,b,c) = \begin{pmatrix} q^{\binom{b}{2}} \binom{b+c}{b}_... ... \cdots & q^{\binom{b}{2}} \binom{b+c}{b}_q \\ \end{pmatrix}; \end{displaymath}$

por indu��o, basta mostrar que

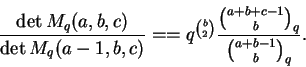
$\begin{displaymath}\frac{\det M_q(a,b,c)}{\det M_q(a-1,b,c)} = = q^{\binom{b}{2}} \frac{\binom{a+b+c-1}{b}_q}{\binom{a+b-1}{b}_q}. \end{displaymath}$

Defina

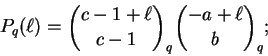
$\begin{displaymath}P_q(\ell) = \binom{c-1+\ell}{c-1}_q \binom{-a+\ell}{b}_q; \end{displaymath}$

observe que $P_q(\ell)$ pode ser escrito como $P(q^\ell)$ onde $P \in {\mathbb{C} }(q)[X]$ tem grau b+c-1. Temos $P_q(-c+1) = P_q(-c+2) = \cdots = P_q(-2) = P_q(-1) = 0$ , $P_q(a) = P_q(a+1) = \cdots = P_q(a+b-2) = P_q(a+b-1) = 0$ e

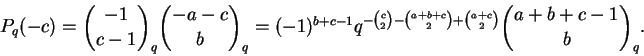
$\begin{displaymath}P_q(-c) = \binom{-1}{c-1}_q \binom{-a-c}{b}_q = (-1)^{b+c-1}... ...{2} - \binom{a+b+c}{2} + \binom{a+c}{2}} \binom{a+b+c-1}{b}_q. \end{displaymath}$

Seja $v \in ({\mathbb{C} }(q))^a$ dado por v_i = (-1)ⁱ P_q(a-i-1):

$\begin{displaymath}v = \left({P_q(a-1), -P_q(a-2), \ldots, (-1)^{a-2} P_q(1), (-1)^{a-1} P_q(0)}\right) \end{displaymath}$

ou seja

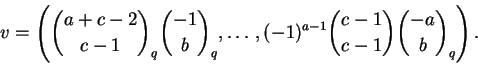
$\begin{displaymath}v = \left({ \binom{a+c-2}{c-1}_q \binom{-1}{b}_q, \ldots, (-1)^{a-1} \binom{c-1}{c-1} \binom{-a}{b}_q }\right). \end{displaymath}$

Temos

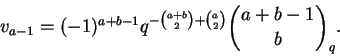
$\begin{displaymath}v_{a-1} = (-1)^{a+b-1} q^{- \binom{a+b}{2} + \binom{a}{2}} \binom{a+b-1}{b}_q. \end{displaymath}$

Se w = M_q(a,b,c) v temos
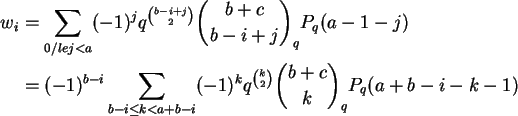
$\begin{align}w_i &= \sum_{0 /le j < a} (-1)^j q^{\binom{b-i+j}{2}} \binom{b+c}{... ...+b-i} (-1)^k q^{\binom{k}{2}} \binom{b+c}{k}_q P_q(a+b-i-k-1) \notag \end{align}$
e usando o corol�rio acima temos que

w_i = (-1)^b-i+1 (S^-_i + S⁺_i)

onde
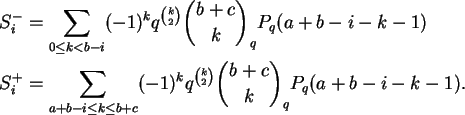
$\begin{align}S^-_i &= \sum_{0 \le k < b-i} (-1)^k q^{\binom{k}{2}} \binom{b+c}{k... ...b+c} (-1)^k q^{\binom{k}{2}} \binom{b+c}{k}_q P_q(a+b-i-k-1). \notag \end{align}$
Mas se $0 \le k < b-i$ temos $a \le a+b-i-k-1 < a+b$ , assim P_q se anula em todos os termos do somat�rio que define S^-_ie temos S^-_i = 0 para qualquer valor de i. Por outro lado, se i < a-1 e $a+b-i \le k \le b+c$ temos -c < a+b-i-k-1 < 0 e P se anula agora em todos os termos do somat�rio que define S⁺_i. Assim temos w_i = 0 para i < a-1. Se i = a-1, o �nico termo do somat�rio S⁺_i que n�o se anula � para k = b+c e temos
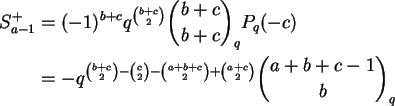
$\begin{align}S^+_{a-1} &= (-1)^{b+c} q^{\binom{b+c}{2}} \binom{b+c}{b+c}_q P_q(-... ...{2} - \binom{a+b+c}{2} + \binom{a+c}{2}} \binom{a+b+c-1}{b}_q \notag \end{align}$
e

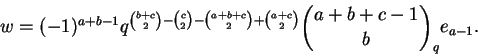
$\begin{displaymath}w = (-1)^{a+b-1} q^{\binom{b+c}{2} -\binom{c}{2} - \binom{a+b+c}{2} + \binom{a+c}{2}} \binom{a+b+c-1}{b}_q e_{a-1}. \end{displaymath}$

Podemos escrever v = (M_q(a,b,c))^-1 wdonde

$\begin{displaymath}(M_q(a,b,c))^{-1} e_{a-1} = (-1)^{a+b-1} q^{- \binom{b+c}{2} ... ...inom{a+b+c}{2} - \binom{a+c}{2}} {\binom{a+b+c-1}{b}_q}^{-1} v.\end{displaymath}$

Assim, a entrada (a-1,a-1) de (M_q(a,b,c))^-1 �

$\begin{displaymath}q^{- \binom{a+b}{2} + \binom{a}{2} - \binom{b+c}{2} + \binom{... ...{\binom{b}{2}} \frac{\binom{a+b-1}{b}_q}{\binom{a+b+c-1}{b}_q} \end{displaymath}$

pois

$\begin{displaymath}\binom{a+b+c}{2} - \binom{a+b}{2} - \binom{a+c}{2} + \binom{a... ...= \binom{b+c}{2} - \binom{b}{2} - \binom{c}{2} + \binom{0}{2}; \end{displaymath}$

de fato, basta observar que $\binom{x}{2}$ � um polin�mio de grau 2. Mas por Cramer esta entrada � $\det M_q(a-1,b,c) / \det M_q(a,b,c)$ , o que conclui a demonstra��o. $\blacksquare$

Next: Coberturas por domin�s e Up: Domin�s e q-contagem Previous: N�meros binomiais

Nicolau C. Saldanha
1999-08-10