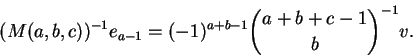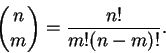
Vamos começar com uma definição usual.
Definição 1.1:
Definimos os números binomiais pela fórmula
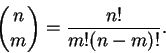
Outras possíveis definições são a recursiva e a algébrica, que enunciaremos como proposições.
Proposição 1.2:
Os números binomiais satisfazem
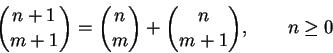

Dem: Indução.
![]()
Proposição 1.3: (Binômio de Newton)
Para todo
![]() vale a identidade de polinômios
vale a identidade de polinômios
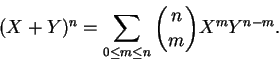
Dem: Indução.
![]()
Observemos ainda que
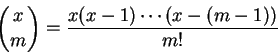
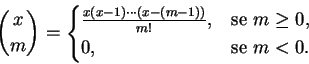
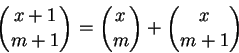
Existem inúmeras interpretações combinatórias para números binomiais:
a mais conhecida é que
![]() é o número de subconjuntos
de m elementos de um conjunto de n elementos dado
(por exemplo,
é o número de subconjuntos
de m elementos de um conjunto de n elementos dado
(por exemplo,
![]() ).
Outra interpretação interessante
é como o número de caminhos de comprimento n (o valor mínimo)
ligando (0,m) e (n-m,0)andando sempre por retas verticais ou horizontais inteiras,
conforme ilustrado abaixo.
Uma demonstração bijetiva deste fato consiste em tomar para cada caminho
o conjunto das posições ao longo do caminho dos segmentos verticais:
este é um subconjunto de m elementos de
).
Outra interpretação interessante
é como o número de caminhos de comprimento n (o valor mínimo)
ligando (0,m) e (n-m,0)andando sempre por retas verticais ou horizontais inteiras,
conforme ilustrado abaixo.
Uma demonstração bijetiva deste fato consiste em tomar para cada caminho
o conjunto das posições ao longo do caminho dos segmentos verticais:
este é um subconjunto de m elementos de
![]() .
O caminho na figura abaixo corresponde ao subconjunto
.
O caminho na figura abaixo corresponde ao subconjunto
![]() .
.

Existem muitíssimas identidades interessantes envolvendo números binomiais. Enunciaremos agora algumas que serão usadas mais adiante.
Proposição 1.4:
Para quaisquer
![]() ,
,
![]() e
e
![]() temos
temos
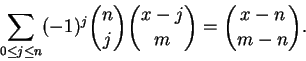
Dem:
Por indução em n, sendo trivial o caso n = 0.
O caso n = 1 é a identidade recursiva da Proposição 1.2
(apenas mudando o nome das variáveis):
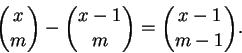
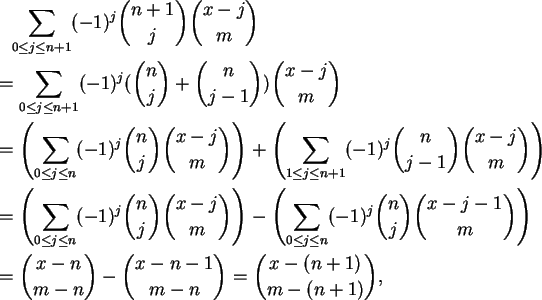
Corolário 1.5:
Seja
![]() um inteiro positivo e
um inteiro positivo e
![]() ,
,
![]() ,
um polinômio de grau menor do que n. Então
,
um polinômio de grau menor do que n. Então
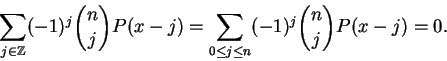
Observe que apenas um número finito de termos do primeiro somatório são diferentes de 0: exatamente aqueles valores considerados no segundo somatório.
Dem:
Podemos escrever
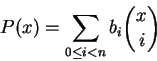
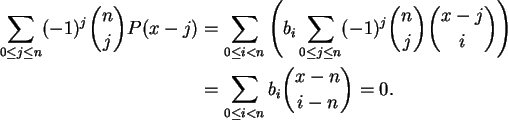
Proposição 1.6:
Para quaisquer naturais a, b, c temos
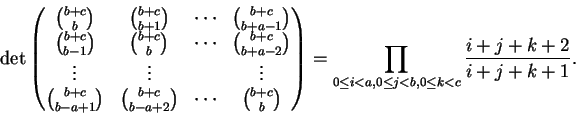
Observe que a matriz é quadrada de ordem a. Observe também que do lado direito os papéis de a, b e csão intercambiáveis, o que não ocorre do lado esquerdo. Por outro lado, o lado esquerdo é claramente inteiro; o leitor pode tentar mostrar diretamente que o lado direito é inteiro.
Na demonstração da proposição usaremos a equação
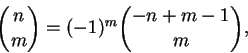
Dem:
Os casos a = 0 e a = 1 são triviais. Definamos
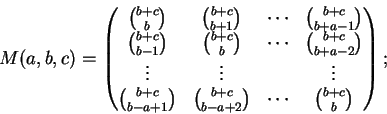
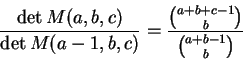
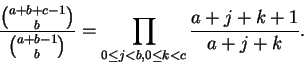
Defina
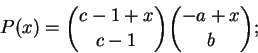
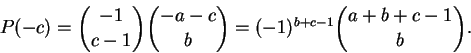
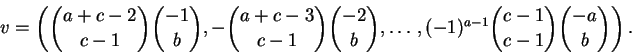
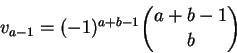
Calculemos a i-ésima coordenada wi de w.
Temos, por uma simples mudança de índices,
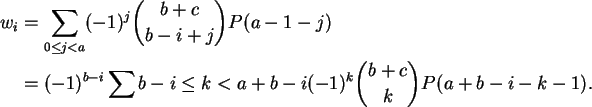
Mas pelo corolário temos
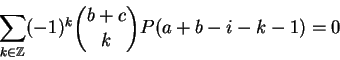
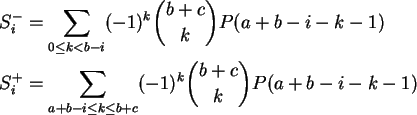
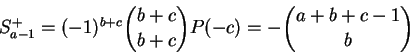
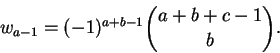
Podemos escrever
v = (M(a,b,c))-1 wdonde