Uma Visão Elementar de Supersimetria

Os físicos teóricos consideram a supersimetria uma idéia tão bela que mesmo na ausência de qualquer indício empírico direto da sua verdade, e somente um indireto de que talvez seja verdade ([Wi]), quase todas as propostas atuais de teorias fundamentais incorporam a supersimetria. Pelas suas propriedades matemáticas e conseqüências físicas marcantes, as teorias supersimétricas destacam-se entre os candidatos mais promissores para a nossa próxima visão do mundo físico. Mas o que é a supersimetria? Não é fácil formular a resposta em termos leigos. Há várias razões para isto. Em primeiro lugar, a supersimetria, do jeito que o físico a entende, combina de uma maneira não trivial a simetria do espaço-tempo e uma relação entre os dois tipos fundamentais de campos físicos, os bosônicos e os fermiônicos ([So]). Há muita especificidade nesta mistura, e isto oculta as propriedades essenciais das estruturas matemáticas envolvidas, apesar destas existirem independentemente de qualquer relação com o espaço-tempo. De fato, todo aluno de matemática já é familiar, sem perceber isto, com vários exemplos delas. Em segundo lugar, uma boa parte de supersimetria é formal, ou seja, tem mais a ver com expressões e não com objetos matemáticos ``verdadeiros''. Simetrias formais não tem muita graça, a qual só aparece com as interpretações. Interpretações em termos de teorias quânticas fundamentais estão longe da experiência leiga. Infelizmente as conseqüências mais notáveis e úteis aparecem só na teoria quântica. Fora deste contexto só um apelo à beleza é capaz de manter interesse. Finalmente, a abordagem matemática correta exige idéias que raramente fazem parte das matérias usuais de cursos de matemática, e o aluno de modo geral tem pouca familiaridade com elas, apesar de muitas serem bastante elementares. Tentaremos, por meio de exemplos simples, apresentar aqui uma visão elementar deste assunto tão extraordinário.

Considere a expressão xy e uma substituição $\phi$ para x e $\psi$ para y. Por exemplo, $\phi=(-x)$ e $\psi=(-y)$ . Temos agora (-x)(-y). É tentador dizer que temos xy de novo, mas com qual justificativa? Uma seria dizer que x e y são números, ou matrizes, ou outros objetos parecidos, e portanto as propriedades elementares destes justificam a conclusão. Ou seja, as expressões são interpretadas e dada a interpretação podemos provar que $\phi\psi = xy$ . Por outro lado, numa abordagem mais formal, podemos introduzir algumas regras pelas quais uma expressão poderia ser transformada numa outra e assim, após um número finito de aplicações destas regras, $\phi\psi$ se transforma em xy. Assim não dizemos o que x e y são mas somente o que pode ser feito com expressões que os envolvem.

Digamos que $\alpha$ e $\beta$ são quaisquer justaposições de símbolos, e admitamos as seguintes regras de reescrita:

$\begin{displaymath}-(-\alpha) \mapsto \alpha, \quad (\alpha)(-\beta) \mapsto -(\alpha)\beta \end{displaymath}$

$\begin{displaymath}(-x)(-y) \mapsto -(-x)y \mapsto xy.\end{displaymath}$

A supersimetria atua em situações intermediárias entre as interpretadas e as formais, onde certos símbolos tem interpretação em termos de objetos matemáticos ``usuais'', e outros não. Isto dá lugar a muita perplexidade em quem aborda o assunto pela primeira vez, especialmente aos estudiosos de matemática que tentam entender a literatura física.

Dado que contemplamos substituições pelas quais $\phi\psi$ pode ser ``transformado'' de volta a xy, ou seja, em que xy é ``invariante'', é tentador dizer que estamos diante de um ``grupo de invariância''. O contexto porém é muito solto e não há necessariamente um grupo a vista. Às vezes achamos grupos e às vezes não. Às vezes achamos algo que tem muitas coisa em comum com grupos mas que estritamente falando não o são. Supergrupos são exemplos destes últimos objetos. Supersimetria na sua abordagem formal é ``simetria'' em relação a um ``grupo'' que de fato não o é. É de fato um tipo de grupo quântico.

Consideremos algumas interpretações de xy. Os símbolos x e y então indicam objetos matemáticos de algum tipo e portanto $\phi$ e $\psi$ devem ser objetos do mesmo tipo. Impomos a condição $\phi\psi = xy$ . Se o tipo é número então simplesmente passamos de um par de números a outro par que tem o mesmo produto. Não há estrutura de grupo evidente nesta situação. Mesmo sendo possível achar um grupo de transformações $(x,y) \mapsto (\phi(x,y) , \psi(x,y))$ para o qual $\phi\psi = xy$ , não é esta a idéia. Não estamos exigindo que $\phi$ e $\psi$ dependam de x e y, simplesmente que os substituam. A situação muda um pouco se x e y agora são interpretados como funções definidas no plano $\hbox{\blackboard R}^2$ , a saber, as funções coordenadas. Neste caso $\phi$ e $\psi$ são funções também e temos $\phi(x,y)\psi(x,y)=xy$ . Há muitos grupos de transformações $(x,y) \mapsto (\phi(x,y) , \psi(x,y))$ que podem ser formados por tais pares de funções. O conjunto de todas as inversíveis que levam cada conjunto de nível da função xy em si mesmo, é o maior grupo deste tipo. Este tem dimensão infinita.

Uma situação mais restrita acontece quando interpretamos x e y como elementos geradores do anel polinomial ${\cal R} =\hbox{\blackboard R}[x,y]$ . Um par de polinômios, $(\phi,\psi)$ , satisfaz $\phi(x,y)\psi(x,y)=xy$ se e só se tem uma das seguintes formas:

$\begin{displaymath}(\lambda, \lambda^{-1}xy),\quad (\lambda^{-1}xy, \lambda), \quad (\lambda x, \lambda^{-1}y),\quad (\lambda y, \lambda^{-1}x) \end{displaymath}$

Um outro caso, ainda em $\hbox{\blackboard R}[x,y]$ , é a expressão x²+y². Agora $\phi$ e $\psi$ são necessariamente polinômios lineares, $\phi(x,y) = ax + by$ e $\psi(x,y) = cx+dy$ , tais que a matriz

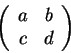
$\begin{displaymath}\left(\begin{array}{cc} a & b \\ c & d\end{array}\right) \end{displaymath}$

Uma situação também interessante acontece se x e y são geradores da álgebra exterior $\Lambda(\hbox{\blackboard R}^2)$ onde por xyentendemos $x\wedge y$ . Temos $\phi = a + bx + cy+dxy$ e $\psi = s + tx + uy +vxy$ . Do $\phi\psi = xy$ deduzimos, as = 0, at+ bs = 0, au + cs = 0, e bu- ct +av+ ds = 1. Entre as soluções destas equações estão aquelas com a=s=d=v=0 e bu- ct=1. Estas definem um grupo isomorfo a $\hbox{SL}(2,\hbox{\blackboard R})$ , dado pelas matrizes

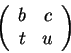
$\begin{displaymath}\left(\begin{array}{cc} b & c \\ t & u \end{array}\right) \end{displaymath}$

O caso de álgebras pode ser considerado algo intermediário entre o interpretado e o formal. Para $\hbox{\blackboard R}[X]$ , por exemplo, não precisamos dizer o que X é, só que algumas regras, tais como Xⁿ X^m = X^n+m, são válidas. Assim há algo de ``formal''. Os coeficientes c_n em $\sum_nc_nX^n$ , porém, são números, e portanto há também algo de ``interpretado''. Uma lição que podemos tirar destes exemplos é que a medida que introduzimos elementos ``formais'' nos objetos designados por x e y, mais possibilidade temos de perceber alguma estrutura de grupo presente, mas pelo fato de ``substituição'' não ser exatamente a mesma coisa que ``transformação'', é possível esperar outras possibilidades.

No resto deste capítulo, vamos explorar algumas estruturas algébricas inspiradas por teorias físicas. A título de conveniência, supomos que todas as álgebras são reais. O caso complexo em geral é uma fácil adaptação, e a maioria das considerações valem para corpos gerais de característica diferente de 2.

A mecânica quântica divide os objetos físicos em bosônicos e fermiônicos. Este fato é expresso algebricamente por comutação de operadores no primeiro caso e por anti-comutação no segundo. Esta diferença é fundamental para toda a teoria.

Lembramos que numa álgebra associativa ${\cal A}$ dizemos que acomuta com b se o comutador [a,b]=ab-ba =0. Dizemos que a anti-comuta com b se o anti-comutador $\{a,b\} = ab+ba = 0$ . Ora, se a e b comutam com c, então ab também comuta com c. Porém, se a e b anti-comutam com c, então ab em geral não anti-comuta com c mas comuta com ele. Mais ainda, se a comuta com c, e b anti-comuta com c (ou vice-versa), então abanti-comuta com c. Se denotamos por ${\cal C}_0$ a subálgebra de elementos que comutam com c, e por ${\cal C}_1$ o subespaço daqueles que anti-comutam com c, então têm-se ${\cal C}_0{\cal C}_0\cup{\cal C}_1{\cal C}_1\subset{\cal C}_0$ e ${\cal C}_0{\cal C}_1\cup{\cal C}_1{\cal C}_0\subset{\cal C}_1$ , o que nos leva a introduzir as álgebras graduadas.

Seja S um semigrupo. Uma álgebra ${\cal A}$ é uma álgebra S-graduada se existem subespaços vetoriais ${\cal A}_s$ para $s\in S$ tais que ${\cal A}=\oplus_{s\in S}{\cal A}_s$ e ${\cal A}_s{\cal A}_r\subset{\cal A}_{sr}$ . Um elemento $a\in{\cal A}$ é dito homogêneo de grau s se $a\in{\cal A}_s$ . Neste caso denotamos o grau de a por |a|. No que segue, vamos introduzir expressões que são válidas somente para elementos homogêneos, sem chamar atenção para este fato, entendendo que a presença na expressão do grau de um elemento já indica que ele deve ser homogêneo.

Um morfismo entre duas álgebras S-graduadas ${\cal A}$ e ${\cal B}$ é um morfismo de álgebras $\phi$ que preserva a graduação, isto é $\phi({\cal A}_s)\subset {\cal B}_s$ .

A supersimetria utiliza álgebras $\hbox{\blackboard Z}_2$ -graduadas, também conhecidas como superálgebras. Se ${\cal A}$ é uma superálgebra então ${\cal A}_0$ é conhecida como a subálgebra bosônica, e ${\cal A}_1$ como o subespaço fermiônico (o qual não é uma subálgebra). No caso de dimensão finita vamos indicar em geral uma base de ${\cal A}_0$ por $b_1,\dots,b_n$ e uma base de ${\cal A}_1$ por $f_1,\dots,f_m$ , e dizer que ${\cal A}$ é de tipo (n,m).

Seja ${\cal A}$ uma superálgebra. A aplicação bilinear $[ \cdot,\cdot]_s$ definida por

O supercolchete combina propriedades do comutador e do anti-comutador de uma maneira sistemática. Na literatura física vê-se freqüentemente a expressão muito feia, $[a,b\}$ , com o colchete a esquerda e a chave a direita, para denotar o supercomutador.

As propriedades do supercomutador assemelham-se às propriedades do colchete de Lie, porém, com algumas mudanças de sinal. Em primeiro lugar, tem-se a relação de simetria graduada

[a,[b,c]_s]_s+ (-1)^|a|(|b|+|c|)[b,[c,a]_s ]_s+ (-1)^|c|(|a|+|b|)[c,[a,b]_s]_s=0

(3.3)

[a,bc]_s= [a,b]_sc+(-1)^|a||b|b[a,c]_s

(3.4)

(-1)^|a||c|[a,[b,c]_s]_s+ (-1)^|a||b|[b,[ c,a]_s]_s+ (-1)^|c||b|[c,[a,b]_s]_s=0

(3.5)

É notável que o anti-comutador $\{\cdot,\cdot\}$ por si só, não satisfaça nenhuma identidade parecida com a de Jacobi.

Algumas álgebras familiares já são superálgebras de forma natural. A álgebra polinomial real $\hbox{\blackboard R}[X]$ da variável Xé naturalmente $\hbox{\blackboard R}[X^2]\oplus X\hbox{\blackboard R}[X^2]$ . Outros dois exemplos são a álgebra exterior $\Lambda(\hbox{\blackboard V})$ de um espaço vetorial $\hbox{\blackboard V}$ e a álgebra de Clifford ${\cal C}\ell(\hbox{\blackboard V},\beta)$ de um espaço vetorial $\hbox{\blackboard V}$ com uma forma bilinear simétrica não-degenerada $\beta$ . A subálgebra bosônica consiste de somas de produtos (exterior ou de Clifford, conforme o caso) de um número par de elementos de $\hbox{\blackboard V}$ , e o subespaço fermiônico de somas de produtos de um número ímpar. Note que a álgebra comutativa $\hbox{\blackboard R}[X]$ não é supercomutativa, já que $[X,X]_s= 2X^2 \neq 0$ enquanto a álgebra supercomutativa $\Lambda(\hbox{\blackboard V})$ não é comutativa já que para $v,w\in\hbox{\blackboard V}$ tem-se $v\wedge w = - w \wedge v$ .

No mundo de objetos $\hbox{\blackboard Z}_2$ -graduados o análogo correto de comutatividade é a supercomutatividade. Álgebras comutativas no sentido usual devem ser consideradas como essencialmente não comutativas neste contexto.

Uma superálgebra de Lie é uma álgebra $\hbox{\blackboard Z}_2$ -graduada ${\cal A}$ cujo produto, denotado por $[ \cdot,\cdot]_s$ , satisfaz as propriedades (3.2) e (3.5) acima. Qualquer superálgebra associativa é uma superálgebra de Lie com o produto sendo o supercomutador. Uma representação de uma superálgebra de Lie ${\cal A}$ é uma aplicação linear $\phi:{\cal A}\to{\cal B}$ para uma superálgebra associativa ${\cal B}$ , preservando a graduação, tal que

$\begin{displaymath} \phi([a,b]_s)=[\phi(a),\phi(b)]_s= \phi(a)\phi(b)-(-1)^{\vert a\vert\vert b\vert}\phi(b)\phi(a) \end{displaymath}$

(3.6)

Vários teoremas usuais sobre álgebras de Lie têm análogos muito parecidos para superálgebras de Lie. Assim, superálgebras de Lie podem ser representadas universalmente numa superálgebra associativa envolvente. Seja ${\cal A}$ uma superálgebra de Lie e seja $\tilde{\cal A}$ a álgebra tensorial plena do espaço vetorial ${\cal A}$ . Tem-se

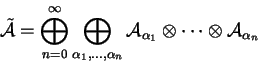
$\begin{displaymath}\tilde{\cal A}=\bigoplus_{n=0}^\infty\bigoplus_{\alpha_1,\dot... ..._n} {\cal A}_{\alpha_1}\otimes\cdots\otimes{\cal A}_{\alpha_n} \end{displaymath}$

Vale também o análogo do teorema de Birkoff-Witt. Seja ${\cal A}$ de tipo (n,m), então uma base para ${\cal U}({\cal A})$ é dado por produtos de forma $b_1^{k_1}\cdots b_n^{k_n}f_1^{\ell_1}\cdots f_m^{\ell_m}$ onde $k_i \geq 0$ são inteiros e $\ell_i\in\{0,1\}$ . O caso de todos os k_i e $\ell_j$ iguais a zero corresponde ao elemento unidade.

Como um exemplo considere a superálgebra de Lie com ${\cal A}_0=\{0\}$ e ${\cal A}_1$ sendo um espaço vetorial qualquer. Neste caso [ a,b ]_s= 0 para qualquer par de elementos, e o ideal ${\cal I}$ é gerado por todos os produtos tensoriais $a\otimes b + b \otimes a$ para todos os $a,b \in {\cal A}_1$ . Disso vê-se que ${\cal U}({\cal A})$ é $\Lambda({\cal A}_1)$ , a álgebra exterior de ${\cal A}_1$ . Como outro exemplo ilustrativo seja ${\cal A}$ de tipo (n,m). Assuma que ${\cal A}_0$ seja uma álgebra de Lie abeliana e que [ b_i,f_j ]_s=0. Temos $[f_i,f_j ]_s= \sum_k c_{ijk}b_k$ . Vemos de (3.1) que c_ijk=c_jik, mas (3.3) não impõe mais nenhuma relação. Considere o caso particular de n=1, m=2 com $[f_1,f_1]_s= 2\alpha b$ , $[f_1, f_2 ]_s= [f_2, f_1 ]_s= \beta b$ , e $[f_2,f_2 ]_s=2\gamma b$ . Em ${\cal U}({\cal A})$ há relações $f_1^2=\alpha b$ , $f_1f_2 + f_2f_1 = \beta b$ , e $f_2^2 =\gamma b$ . É fácil ver que como espaço vetorial tem-se ${\cal U}({\cal A}) = \hbox{\blackboard R}[b] \oplus\hbox{\blackboard R}[b]f_1 \oplus\hbox{\blackboard R}[b]f_2 \oplus \hbox{\blackboard R}[b]f_1f_2$ .

É instrutivo considerar a álgebra de Lie ${\cal L}({\cal A})\subset {\cal U}({\cal A})$ gerada por ${\cal A}$ contida em ${\cal U}({\cal A})$ . Suponha $\alpha=1$ e $\beta=\gamma=0$ . Vamos demonstrar que ${\cal L}({\cal A})$ contém todos os monômios de forma b^k f₁para k natural.

Primeiro, [f₁, f₂] = 2f₁f₂, e portanto $f_1f_2 \in {\cal L}({\cal A})$ . Note que b comuta com tudo. Suponha, por indução em n, que bⁿf₂ e bⁿf₁f₂ pertencem a ${\cal L}({\cal A})$ . A hipótese é verdadeira para n=0. De [f₁,f₁f₂]= 2bf₂ tem-se [f₁, bⁿ f₁f₂]=2bⁿ⁺¹f₂ e assim $b^{n+1}f_2\in{\cal L}({\cal A})$ . Também [f₁, bⁿ⁺¹f₂] = 2bⁿ⁺¹f₁f₂ e portanto $b^{n+1}f_1f_2\in{\cal L}({\cal A})$ , o que completa a demonstração.

O ponto essencial deste resultado é que ${\cal L}({\cal A})$ tem dimensão infinita. Assim uma superálgebra de Lie ${\cal A}$ de dimensão finita foi usada para codificar uma álgebra de Lie ${\cal L}({\cal A})$ usual de dimensão infinita.

Interessa à física as simetrias da matriz de espalhamento S. Este é um operador unitário no espaço de Hilbert dos estados físicos que descreve os detalhes de processos elementares. Existem duas noções de simetria, (1) um operador unitário^3.1 U tal que USU^*=S, e (2) um operador auto-adjunto K tal que [K,S]=0. No segundo caso, sob condições adequadas, o grupo unitário $U(\tau)=\exp(i\tau K)$ para $\tau\in\hbox{\blackboard R}$ , fornecido pelo teorema espectral, satisfaz $U(\tau)SU(\tau)^*=S$ , e portanto é um grupo de de simetrias unitárias. Um tal operador K é conhecido como simetria infinitesimal. Formalmente, se K e L são simetrias infinitesimais, então pela identidade de Jacobi temos [[K,L],S]=0. Assim, ainda formalmente, as simetrias infinitesimais, multiplicados pelo número imaginário i, formam uma álgebra de Lie. Na teoria relativista do campo quântico, a álgebra de Lie de simetrias infinitesimais contém, como subálgebras, uma imagem isomorfa à álgebra de Lie do grupo de Poincaré (gerado por translações no espaço-tempo e transformações de Lorentz) e uma álgebra de Lie de dimensão finita de simetrias internas que relaciona propriedades de espécies diferentes de partículas (por exemplo prótons e nêutrons). Esforços iniciais de combinar de uma maneira não trivial as simetrias do espaço-tempo e as simetrias internas, o que daria uma teoria com poder de previsão maior, encontrou um obstáculo no famoso ``no-go theorem'' de Coleman e Mandula ([CM]). Este afirma que na teoria relativista de campo quântico, qualquer álgebra de Lie de dimensão finita de simetrias infinitesimais que estende a simetria de Poincaré, é necessariamente uma soma direta (e portanto uma combinação trivial) da álgebra de Poincaré com a álgebra de simetrias internas. A supersimetria evita este teorema postulando uma superálgebra de Lie de dimensão finita de simetrias infinitesimais, a qual, como vimos no exemplo anterior, é capaz de gerar uma álgebra de Lie de dimensão infinita e portanto foge das hipótese do teorema de Coleman-Mandula.

Retornando ao contexto físico em discussão, uma álgebra de Lie de dimensão finita de simetrias infinitesimais, pode ser, em princípio, exponenciada a uma representação unitária do grupo de Lie correspondente, formando assim um grupo de simetrias unitárias. Se porém temos uma superálgebra de Lie de simetrias infinitesimais, uma exponenciação, em princípio, nos levaria a elementos de um problemático grupo de Lie de dimensão infinita. Seria genial se tivermos um processo análogo ao de exponenciação que resultaria num objeto que codificaria o suposto grupo de Lie de dimensão infinita de maneira parecida com a codificação de álgebras de Lie de dimensão infinita por superálgebras de Lie de dimensão finita. Isto nos leva a considerar supergrupos.

Um espaço vetorial $\hbox{\blackboard Z}_2$ -graduado é um espaço vetorial $\hbox{\blackboard V}$ junto com uma decomposição numa soma direta de dois subespaços $\hbox{\blackboard V}=\hbox{\blackboard V}_0\oplus\hbox{\blackboard V}_1$ . A álgebra $\hbox{End}(\hbox{\blackboard V})$ tem agora uma $\hbox{\blackboard Z}_2$ -graduação natural. Temos $L\in\hbox{End}_i(\hbox{\blackboard V})$ se $L(\hbox{\blackboard V}_j)\subset \hbox{\blackboard V}_{i+j}$ . Em termos de matrizes em blocos temos

$\begin{displaymath} L=\left(\begin{array}{cc} L_{00} & L_{01} \\ L_{10} & L_{11... ...t(\begin{array}{cc} 0 & L_{01} \\ L_{10} & 0\end{array}\right) \end{displaymath}$

(3.7)

Um dos subespaços $\hbox{\blackboard V}_i$ é usualmente considerado como bosônico e o outro como fermiônico, embora a definição não faça distinção entre os dois. A $\hbox{\blackboard Z}_2$ -graduação de $\hbox{End}(\hbox{\blackboard V})$ não depende de qual dos subespaços é identificado como bosônico. Uma tal identificação, quando é feita, tem que ser baseada em considerações adicionais.

Seja ${\cal A}$ uma superálgebra de Lie e $\hbox{\blackboard V}$ um espaço vetorial $\hbox{\blackboard Z}_2$ -graduado. Por uma representação de ${\cal A}$ em $\hbox{\blackboard V}$ entendemos uma representação em $\hbox{End}(\hbox{\blackboard V})$ como definida anteriormente.

Sejam ${\cal A}$ uma superálgebra de Lie, ${\cal B}$ uma superálgebra associativa de dimensão finita e $\lambda:{\cal A}\to{\cal B}$ uma representação. Temos as exponenciais $\exp(\lambda(a))\in{\cal B}$ , mas em geral não podemos compô-las: $\exp(\lambda(a))\exp(\lambda(b))$ em geral não é da forma $\exp(\lambda(c))$ para algum $c\in {\cal A}$ , nem para o caso de a e b serem restritos a uma vizinhança suficientemente pequena de zero, como seria o caso de álgebras de Lie usuais.

$\begin{displaymath} \exp(A)\exp(B) = \exp(C) = \exp\left(\sum_{n=1}^\infty\frac{1}{n!} C_n\right) \end{displaymath}$

(3.8)

$\begin{displaymath}C=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]+\frac{1}{12}[B,[B,A]]) + \cdots\end{displaymath}$

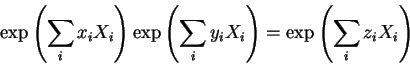
$\begin{displaymath}\exp\left(\sum_i x_i X_i\right)\exp\left(\sum_i y_i X_i\right)= \exp\left(\sum_i z_i X_i\right) \end{displaymath}$

Sejam ${\cal A}$ e ${\cal B}$ duas superálgebras. Definimos o produto tensorial $\hbox{\blackboard Z}_2$ -graduado ${\cal A}\hat\otimes{\cal B}$ . Como espaço vetorial, ${\cal A}\hat\otimes{\cal B}$ é o produto tensorial ${\cal A}\otimes{\cal B}$ usual. A multiplicação, porém, é definida por

$\begin{displaymath}(a\otimes b)(c\otimes d)=(-1)^{\vert b\vert\vert c\vert}ac\otimes bd \end{displaymath}$

$\begin{displaymath}[a\otimes b, c\otimes d ]_s= (-1)^{\vert b\vert\vert c\vert}\... ...ert\vert c\vert} ca\otimes[b,d ]_s+[a,c ]_s\otimes bd \right) \end{displaymath}$

(3.9)

Consideremos agora que b e d são ``elementos'' com propriedades fixas a-priori e que a e c são ``coeficientes'' cujas propriedades podemos escolher à vontade. Se estamos interessados nas propriedades dos ``elementos'' em relação ao supercolchete, então o lado direito tem o supercolchete conveniente [b, d ]_s mas também o produto incômodo bd. Porém, se assumirmos que ${\cal A}$ é supercomutativo, então [a,c ]_s= 0 e temos

$\begin{displaymath}[a\otimes b, c\otimes d ]_s= (-1)^{\vert b\vert\vert c\vert} ac\otimes[b,d ]_s \end{displaymath}$

(3.10)

Baseado nestas considerações, é de fato fácil provar que se ${\cal A}$ é uma superálgebra supercomutativa e ${\cal L}$ é uma superálgebra de Lie, então ${\cal A}\hat\otimes{\cal L}$ é uma superálgebra de Lie se definirmos o supercolchete por (3.10). Note que a subálgebra bosônica, que é uma álgebra de Lie usual, corresponde a |a|=|b| e |c|=|d|, e assim tanto a parte bosônica quanto a fermiônica de ${\cal L}$ , isto é a superálgebra de Lie inteira, é codificada na álgebra de Lie usual $({\cal A}\hat\otimes{\cal L})_0$ . Isto nos permite usar a formula de Baker-Campbell-Hausdorff para tratar superálgebras de Lie.

Ao introduzir superálgebras, descobrimos que para explorar as suas propriedades somos forçados a estender a idéia de $\hbox{\blackboard Z}_2$ -graduação a quase todos os outros objetos matemáticos em volta. Assim entramos no mundo da ``supermatemática'', com superespaços, supervariedades, etc. O prefixo ``super'', que soa tão pomposo, significa simplesmente ``estendido para objetos $\hbox{\blackboard Z}_2$ -graduados''. Vem junto a idéia de que os elementos ``fermiônicos'' de qualquer um destes objetos anticomutam, e que as noções, e definições da matemática costumeira devem ser modificados pela introdução de um sinal negativo cada vez que uma permuta de dois elementos fermiônicos aparece nas fórmulas usuais. Assim comutador vira anticomutador para elementos fermiônicos, a identidade de Jacobi vira a identidade (3.3) e assim por diante.

Interprete agora a soma $A=\sum_i x_i b_i + \sum_j \theta_jf_j$ como $A=\sum _i x_i\otimes b_i + \sum_j \theta_j\otimes f_j$ onde os x_i e $\theta_j$ são bases para o subespaço bosônico e fermiônico respectivamente de uma superálgebra associativa supercomutativa que denotaremos por ${\cal R}^{[n\vert m]}$ .

Podemos agora interpretar A como um elemento de ${\cal R}^{[n\vert m]}\hat\otimes{\cal A}$ . Do mesmo jeito $B=\sum_i y_i b_i + \sum_j \eta_if_j$ pode ser reescrito como $B=\sum_ i y_i\otimes b_i + \sum_j \eta_j\otimes f_j$ e interpretado também como elemento de ${\cal R}^{[n\vert m]}\hat\otimes{\cal A}$ . Infelizmente se precisamos trabalhar com A e B ao mesmo tempo, não podemos considerar os dois como elementos de ${\cal R}^{[n\vert m]}\hat\otimes{\cal A}$ . Podemos porém considerar todos os coeficientes como elementos de ${\cal R}^{[2n\vert 2m]}$ e assim tanto A quanto B como elementos de ${\cal R}^{[2n\vert 2m]}\hat\otimes{\cal A}$ .

Aplicando agora a formula de Baker-Campbell-Hausdorff a e^Ae^B e usando (3.10), vemos que podemos escrever e^Ae^B=e^Conde $C=\sum_i z_i\otimes b_i + \sum_j \zeta_j\otimes f_j$ e os coeficientes z_i e $\zeta_j$ são séries formais de potências em x_i, y_i, $\theta_j$ e $\eta_j$ . Tais séries formais podem ser um pouco simplificadas. Devido à natureza anticomutativa dos elementos fermiônicos de ${\cal R}^{[2n\vert 2m]}$ , qualquer produto destes com mais que 2m elementos é zero e qualquer outro produto é igual a um da forma $\theta_1^{\mu_1}\theta_2^{\mu_2}\cdots\theta_m^{\mu_m} \eta_1^{\nu_1}\eta_2^{\nu_2} \cdots\eta_m^{\nu_m}$ onde $\mu_i,\,\nu_j\in\{0,1\}$ . Escreva este produto como $\theta ^\mu\eta^\nu$ . Temos então $z_i = \sum_{\mu\nu}z_{i{\mu\nu}}\theta^\mu\eta^\nu$ e $\zeta_j = \sum_{\mu\nu}\zeta_{j{\mu\nu}}\theta^\mu\eta^\nu$ onde cada $z_{i{\mu\nu}}$ e $\zeta_{j{\mu\nu}}$ é uma série formal de potências agora somente nos x_i e y_i.

Neste ponto podemos adotar uma de duas atitudes. A primeira (que pode ser chamada de ``híbrida'') é considerar os x_i e y_i como variáveis reais, do mesmo jeito que acontece no caso de álgebra de Lie. Neste caso as séries formais convergem para |x_i| e |y_j|suficientemente pequenos. Temos então uma coisa parecida com uma lei de produto de um grupo de Lie local: de fato, os z_i00 definem precisamente uma tal lei. Isto pode ser elaborado para definir um supergrupo de Lie como sendo um grupo de Lie cuja álgebra de Lie é precisamente a subálgebra bosônica ${\cal L}_0$ e que possui estrutura adicional para levar em conta o subespaço fermiônico ${\cal L}_1$ . A outra atitude é continuar considerando os x_i e y_i como elementos bosônicos de uma superálgebra supercomutativa e considerar que o processo de exponenciação gera um supergrupo de Lie formal análogo a um grupo de Lie formal.

Não vamos explorar em profundidade nenhuma destas atitudes. A híbrida é que prevalece na literatura física e portanto vamos adotá-la no restante deste capítulo. Apresentamos agora alguma nomenclatura e algumas convenções da literatura física. Dada a álgebra ${\cal R}^{[n\vert m]}$ , o subespaço $\hbox{\blackboard R}^{[n\vert m]}$ gerado por $x_1,\dots,x_n$ e $\theta_1,\dots,\theta_m$ é conhecido como superespaço. Os x_i e os $\theta_j$ são conhecidos como coordenadas do superespaço. Já que um elemento geral da álgebra tem a forma $F = \sum_\mu f_\mu\theta^\mu$ onde os $f_\mu$ são polinômios em $x_1,\dots,x_n$ , dizemos mais geralmente que $F(x,\theta)$ é uma superfunção, ou uma função no superespaço se é da forma $F(x,\theta) =\sum_\mu f_\mu(x)\theta^\mu$ onde os $f_\mu$ são agora simplesmente funções reais de x e não mais restritos a ser polinômios. Uma superfunção então é simplesmente uma coleção de funções reais. O conjunto de superfunções obviamente forma uma nova álgebra que estende ${\cal R}^{[n\vert m]}$ . A derivada parcial de F em relação a x_i é definida da maneira natural,

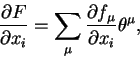$\begin{displaymath}\frac{\partial F}{\partial x_i} = \sum_\mu \frac{\partial f_\mu}{\partial x_i}\theta^\mu, \end{displaymath}$

(3.11)

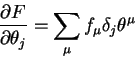$\begin{displaymath}\frac{\partial F}{\partial \theta_j} = \sum _\mu f_\mu\delta_j\theta^\mu \end{displaymath}$

(3.12)

$\begin{displaymath}\frac{\partial}{\partial \theta_1}\theta_1\theta_2=\theta_2, ... ... \frac{\partial}{\partial \theta_2}\theta_1\theta_2=-\theta_1 \end{displaymath}$

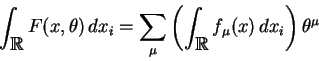
$\begin{displaymath}\int_{\hbox{\blackboard R}}F(x,\theta)\,dx_i = \sum_\mu\left(\int_{\hbox{\blackboard R}}f_\mu(x)\,dx_i\right)\theta^\mu\end{displaymath}$

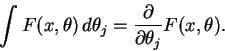
$\begin{displaymath}\int F(x,\theta)\,d\theta_j = \frac{\partial}{\partial \theta_j}F(x,\theta).\end{displaymath}$

$\begin{displaymath}\int \theta\, d\theta = 1, \quad \int d\theta = 0.\end{displaymath}$

Esta regra, em analogia com a integral de Lebesgue, é adotada para fazer a integral invariante em relação a translação por qualquer elemento fermiônico $\eta$ que anticomute com todos os $\theta_k$ .

$\begin{displaymath}\int F(x,\dots,\theta_j+\eta,\dots)\,d\theta_j= \int F(x,\dots,\theta_j,\dots)\,d\theta_j\end{displaymath}$

$\begin{displaymath}\int\cdots\int F(x,\theta)\,dx_1dx_2\cdots dx_nd\theta_1d\the... ...\theta_m = \int\cdots\int f_{1\cdots 1}(x)\,dx_1dx_2\cdots dx_n\end{displaymath}$

$\begin{displaymath}F(X_1(x,\theta),\dots,X_n(x,\theta), \Theta_1(x,\theta),\dots,\Theta_m(x,\theta))\end{displaymath}$

$\begin{displaymath}X_i(x,\theta) = \xi_i(x) + \zeta_i(x,\theta)\end{displaymath}$

$\begin{displaymath} f(X(x,\theta))= \sum_\alpha \frac{\partial^{\alpha_1+\cdots... ...a_n}}(\xi(x)) (\zeta_1)^{\alpha_1}\cdots (\zeta_n)^{\alpha_n} \end{displaymath}$

(3.13)

Passamos agora a considerar certos exemplos simples. Seja ${\cal L}$ de tipo (1,1). Suponha que o único supercolchete não zero entre os geradores seja [f,f]_s= 2b. Agora é fácil calcular pela formula de Baker-Campbell-Hausdorff que

$\begin{displaymath} \exp(xb+\theta f) \exp(yb+\eta f_1)= \exp((x+y-\theta\eta)b + (\theta+\eta)f) \end{displaymath}$

(3.14)

$\begin{displaymath} (x,\theta)\cdot(y,\eta) = (x+y- \theta\eta,\theta+\eta) \end{displaymath}$

(3.15)

Vamos denotar este supergrupo por $\hbox{\blackboard G}$ . Servirá como exemplo para o resto deste capítulo.

O produto ingênuo (3.15) deixa muito a desejar. A medida que ``multiplicamos'' cada vez mais elementos, precisamos introduzir uma superálgebra ${\cal R}^{[k\vert k]}$ cada vez maior para expressar um número cada vez maior de ``valores de parâmetros''. Em geral, nenhum número finito de variáveis pode dar conta da estrutura algébrica de um supergrupo nesta visão ingênua, pois, como já vimos, a álgebra de Lie em ${\cal U}({\cal L})$ gerado por ${\cal L}$ tem dimensão infinita em geral, e assim, qualquer ``produto de grupo'' de dimensão finito é incapaz de capturar o conteúdo matemático de um supergrupo. Interpretando xe y como números reais não ajuda pois as variáveis fermiônicas não podem ser interpretados desta maneira e assim somas como $x+y-\theta\eta$ não teriam nenhuma interpretação clara.

A literatura física de modo geral simplesmente ignora estes fatos, pois as regras para fazer cálculos com superalgebras são de qualquer maneira bastante claras e eficazes. Uma abordagem um pouco mais sistemática é apresentada em ([DeW]) onde, em primeiro lugar, introduz-se um estoque infinito de variáveis fermiônicas $\zeta_1,\zeta_2,\dots$ e, em segundo lugar, a noção de número complexo é estendida a tais chamados supernúmeros que são somas z= z_b+z_s onde $z_b\in \hbox{\blackboard C}$ e z_s é uma série formal com coeficientes complexos de produtos finitos dos $\zeta_i$ . Num gesto poético, z_b é chamado o ``corpo'' de z e z_s a ``alma''. Embora isto produza um cálculo formal bem definido, deixa muito a desejar quanto a matemática.

Felizmente todas as dificuldades podem ser facilmente resolvidas se interpretamos supegrupos em termos de álgebras de Hopf. Deste ponto de vista se grupos clássicos são álgebras de Hopf comutativas, então supergrupos são superálgebras de Hopf supercomutativas. A álgebra universal envolvente de uma álgebra de Lie é, de uma forma natural, uma álgebra de Hopf cocomutativa na qual o processo de exponenciação para o grupo de Lie formal correspondente é simplesmente a passagem para o dual, que é uma álgebra de Hopf comutativa. O caso de superálgebras de Lie está em perfeita analogia com isto. Não vamos porém desenvolver aqui esta teoria. Veja ([Ko]) para um tratamento da ``supermatemática'' em termos de superálgebras de Hopf.

Agora que chegamos a um entendimento elementar de supergrupos, estamos prontos para abordar o conceito de supersimetria. Primeiro devemos entender o que seria uma ação de um supergrupo. Adotando a idéia de que todos os objetos devem ser entendidos como ``superobjetos'', isto é, a abordagem inteira deve ser em termos de $\hbox{\blackboard Z}_2$ -graduação, o objeto mais simples sobre o qual um supergrupo poderia agir parece ser o superespaço $\hbox{\blackboard R}^{[n\vert m]}$ . Na literatura física o superespaço é descrito como um ``espaço no qual, além de um conjunto de coordenadas comutativas usuais $x_1,\dots,x_n$ , há também um conjunto de coordenadas anti-comutativas $\theta_1,\dots,\theta_m$ ''. Nas teorias físicas os $x_1,\dots,x_n$ são considerados coordenadas de um ponto no espaço-tempo e portanto o superespaço é visto como uma extensão do espaço tempo. Não vamos tentar aqui dar qualquer sentido a esta idéia além de puramente metafórico ou formal, apesar de que a idéia possa ser levada mais a sério. Os superespaços estão entre os exemplos mais simples de ``geometrias não comutativas'', mas por serem supercomutativas ainda devem ser consideradas ``clássicas''.

Vamos abordar aqui uma versão ingênua de ação. Já que os nossos supergrupos são ``exponenciações'' de superálgebras de Lie, é natural tentar definir uma ação de um supergrupo ``exponenciando'' uma representação de uma superálgebras de Lie ${\cal L}$ de tipo (n,m). Sejam $\hbox{\blackboard V}$ um espaço vetorial $\hbox{\blackboard Z}_2$ -graduado e $\hat\cdot:{\cal L}\to \hbox{End}(\hbox{\blackboard V})$ um homomorfismo de superálgebras. Ingenuamente a ``ação'' de um ``elemento'' $\exp (t_1b_1+\cdots t_nb_n + \theta_1f_1 + \cdots \theta_mf_m)$ do supergrupo sobre um elemento $v\in \hbox{\blackboard V}$ seria dado por $\exp (t_1\hat b_1+\cdots+ t_n\hat b_n + \theta_1\hat f_1 + \cdots +\theta_m\hat f_m)v$ . Como antes, adotando a atitude híbrida podemos considerar os t_i como números reais, mas os $\theta_i$ devem ser considerados objetos externos.

Vamos agora construir um ação do nosso supergrupo $\hbox{\blackboard G}$ . Como b comuta com tudo, temos que $\exp(t\hat b+\theta\hat f)=\exp(t\hat b)\exp(\theta \hat f)$ . Dado que $(\theta f)^2=0$ , o segundo fator é formalmente igual a $I+\theta \hat f$ . Assim

$\begin{displaymath}\exp(t\hat b+\theta\hat f)=\exp(tb)(I+\theta \hat f)\end{displaymath}$

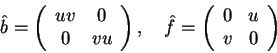$\begin{displaymath}\hat b = \left(\begin{array}{cc} uv & 0 \\ 0 & vu \end{array}... ... f = \left(\begin{array}{cc} 0 & u \\ v & 0 \end{array}\right) \end{displaymath}$

(3.16)

$\begin{displaymath} \exp(t\hat b+\theta\hat f): (x,\alpha)\mapsto e^{tuv}(x+u\theta \alpha, \alpha + v\theta x) \end{displaymath}$

(3.17)

Representações em $\hbox{\blackboard R}^{[2\vert 2]}$ são mais interessantes. Um caso particularmente instrutivo é dado por

$\displaystyle \hat b: (x,y,\alpha,\beta)$	$\textstyle \mapsto$	$\displaystyle (-y, x, -\beta, \alpha)$	(3.18)
$\displaystyle \hat f: (x,y,\alpha,\beta)$	$\textstyle \mapsto$	$\displaystyle (\alpha, \beta, -y,x )$	(3.19)

$\begin{displaymath} (x,y,\alpha,\beta) \mapsto(x+\theta\alpha, y+\theta\beta, \alpha-\theta y, \beta + \theta x) \end{displaymath}$

(3.20)

$\begin{displaymath} x^2+y^2+2\alpha\beta \end{displaymath}$

(3.21)

$\begin{displaymath}(x+\theta\alpha)^2+ (y+\theta\beta)^2 +2(\alpha-\theta y) (\beta + \theta x) \end{displaymath}$

Para apreciar como a física constrói teorias supersimétricas de campos quânticos, é preciso elaborar um pouco mais as nossa construções. As teorias física são quase exclusivamente lagrangianas. Isto quer dizer que são determinadas por um funcional dos campos. Para simplicidade suponha que $\phi(x)$ é um campo escalar e $x\in \hbox{\blackboard R}^4$ é um ponto do espaço-tempo com x₄sendo o tempo. Seja $\phi_i(x)$ a derivada parcial de $\phi$ em relação a x_i. Uma função de $\phi(x)$ e das suas derivadas, ${\cal L}(\phi(x),\phi_1(x),\phi_2(x),\phi_4(x),\phi_4(x))$ , onde ${\cal L}(v_0,v_1,v_2,v_3,v_4)$ é uma função em $\hbox{\blackboard R}^5$ , chama-se uma lagrangiana de $\phi$ . A integral $S(\phi)=\int_{\hbox{\blackboard R}^4}{\cal L}(\phi(x),\phi_i(x))dx$ chama-se o funcional ação de $\phi$ (não confunda este uso da palavra ``ação'' com ação de grupo e outros conceitos semelhantes). Um campo $\phi$ é um ponto crítico deste funcional (no sentido de cálculo de variações) se e somente se satisfaz a equação de Euler-Lagrange:

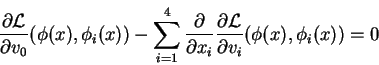
$\begin{displaymath}\frac{\partial {\cal L}}{\partial v_0}(\phi(x),\phi_i(x))-\su... ...x_i}\frac{\partial {\cal L}}{\partial v_i}(\phi(x),\phi_i(x))=0\end{displaymath}$

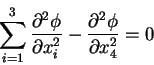
$\begin{displaymath}\sum_{i=1}^3\frac{\partial^2 \phi}{\partial x_i^2} -\frac{\partial^2 \phi}{\partial x_4^2}=0\end{displaymath}$

Considere agora uma ação $\phi\mapsto g\cdot \phi$ de um grupo de Lie G sobre os campos. Dizemos que a teoria lagrangiana é simétrica por ação de G se o conjunto de soluções das equações de Euler-Lagrange é invariante. Em determinadas condições, para criar uma teoria simétrica, é suficiente que a ação $S(\phi)$ seja invariante, isto é $S(g\cdot \phi)=S(\phi)$ . É portanto importante poder achar integrais de funções de campos e suas derivadas que são invariantes por ação de grupos de Lie. Este é um assunto próprio já suficientemente sofisticado que não podemos abordar aqui. Apresentamos somente um exemplo simples. Seja $A=\sum_{i=1}^3A_i\,dx_i$ uma 1-forma em $\hbox{\blackboard R}^3$ e seja G o grupo $\hbox{SO}(3)$ de rotações que age sobre A de modo usual de mudança de coordenadas, a saber, se $R\in\hbox{SO}(3)$ então $(R\cdot A)(Rx) = A(x)$ . Em termos de componentes (A₁,A₂,A₃) temos então $(R\cdot A)_i(x)= \sum_jR_{ij}A_j(R^{- 1}x)$ . Usando o produto interno usual em $\hbox{\blackboard R}^3$ como métrica Riemanniana, fica óbvio que a integral de ||A||² e ||dA||² são invariantes por esta ação e que a integral de A₁² não o é. No caso particular de $A = d\phi$ , temos a lagrangiana $\vert\vert d\phi\vert\vert^2$ com a equação de Euler-Lagrange sendo $\Delta \phi=0$ .

Teorias supersimétricas são aquelas cujo funcional S é invariante sob ação de supergrupos. Os campos agora são funções definidos não no espaço-tempo mas no superespaço que estende espaço-tempo. Aparece porém mais uma consideração que também vem da física quântica. Como já falamos, existem dois tipos de campos quânticos fundamentais, os bosônicos e os fermiônicos. O valor do campo no superespaço portanto também deve pertencer a um superespaço, isto é, poderia ter componentes bosônicos e fermiônicos.

Retornamos ao nosso simples exemplo em $\hbox{\blackboard R}^{[1\vert 1]}$ . Por uma função neste superespaço $\Lambda(x,\alpha)$ nós já entendemos uma expressão $f(x) + g(x)\alpha$ onde f e gsão funções reais. Agora devemos considerar que $f(x) = F(x) + \phi(x)$ e $g(x) = G(x) + \psi(x)$ onde $\phi(x)$ e $\psi(x)$ são fermiônicos. Com isto, e com a idéia que estamos ainda lidando com a situação clássica, e tomando a atitude híbrida, podemos considerar que F e G são funções reais mas que $\phi(x)$ e $\psi(x)$ pertencem a uma superalgebra supercomutativa sem que haja qualquer relação entre estes elementos além de anticomutatividade. Ou seja, estamos contemplando uma superálgebra supercomutativa com um número não enumerável de geradores fermiônicos, a saber, alem do $\alpha\in{\cal R}^{[1\vert 1]}$ todos os $\phi(x)$ e $\psi(x)$ para $x\in \hbox{\blackboard R}$ . A literatura física diz que $\psi$ e $\phi$ são campos com ``valores grassmanianos''. Como base de regras formais de reescrita isto não deve causar nenhuma objeção, mas a interpretação destes objetos dentro de construções matemáticas mais estruturadas ainda é um ponto polêmico ([Sc]).

O nosso supergrupo $\hbox{\blackboard G}$ age sobre $(x,\alpha)$ pela regra (3.17), mas devemos também considerar que possa agir sobre os ``componentes'' $(F, G, \phi, \psi)$ em cada ponto como acontece com a ação de SO(3) sobre os componentes de uma 1-forma, como discutido acima. Assim por exemplo a ação $\Lambda\mapsto\tilde\Lambda$ do ``elemento'' $I+\theta f$ de $\hbox{\blackboard G}$ , seria dado por

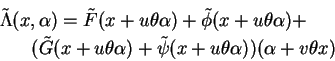
$\begin{eqnarray*}\lefteqn{\tilde\Lambda(x,\alpha) = \tilde F(x+u\theta \alpha) +... ...eta \alpha) + \tilde \psi(x+u\theta \alpha))(\alpha + v\theta x) \end{eqnarray*}$

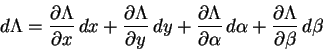
$\begin{displaymath}d\Lambda=\frac{\partial \Lambda}{\partial x}\,dx+ \frac{\part... ...lpha}\,d\alpha+ \frac{\partial \Lambda}{\partial \beta}\,d\beta\end{displaymath}$

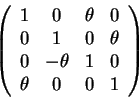
$\begin{displaymath}\left(\begin{array}{cccc} 1 & 0 & \theta & 0 \\ 0 & 1 & 0 &... ... 0 & -\theta & 1 & 0 \\ \theta & 0 & 0 & 1 \end{array}\right)\end{displaymath}$

$\begin{displaymath}\int\int\int\int<d\Lambda,d\Lambda>\, dxdyd\alpha d\beta\end{displaymath}$

$\begin{displaymath}2\int\int(\nabla F\cdot \nabla G + \nabla\phi \cdot\nabla\psi + G^2)\,dxdy\end{displaymath}$

Neste ponto podemos esquecer os passos que levaram a esta integral e simplesmente considerá-lo como o funcional de um problema de cálculo de variações clássico cujas equações de Euler- Lagrange são

$\displaystyle \Delta F = 2G,$	$\textstyle \quad$	$\displaystyle \Delta G =0$	(3.22)
$\displaystyle \Delta \phi = 0,$	$\textstyle \quad$	$\displaystyle \Delta \psi =0$	(3.23)

Toda a máquina de supersimetria agora desapareceu e podemos encarar a supersimetria como simplesmente uma maneira de construir lagrangianas. As propriedade marcantes de sistemas físicos supersimétricos somente aparecem na teoria quântica, portanto equações acima são muito sem graça. O exemplo também é muito simplificado. O que é extraordinário é que os sistemas assim construídos por meio de supersimetria que estendem a simetria clássica do espaço-tempo não só constituem candidatos muito atraentes para teorias físicas básicas, mas também têm fornecido instrumentos para novas descobertas na matemática pura como invariantes de nós, tranças e variedades de dimensão três e quatro.

Podemos agora, pelo menos em palavras, resumir o que são as teorias físicas supersimétricas. São sistemas lagrangianos de campos físicos que podem ser descritos da seguinte maneira:

Uma lagrangiana é supersimétrica se é invariante por um conjunto de regras de reescrita. Embora o funcional ação de um conjunto de campos seja escrito como $\int {\cal L}\,dx_1\cdots dx_n d\theta_1 \cdots d\theta_m$ , para saber se isto é supersimétrico ou não, não é necessário interpretar nem os campos, nem as coordenadas no superespaço, nem a integral. Não é necessário saber o que são estas coisas. Temos simplesmente uma expressão, mais sofisticada que o nosso xy no início, é verdade, mas nada essencialmente diferente. A expressão é invariante por um conjunto de regras de reescrita que são ditadas por uma superálgebra de Lie. Eis a supersimetria neste nível. Uma vez que a teoria é quantizada, a superalgebra de Lie que deu lugar ao conjunto de regras de reescrita agora se incorpora numa superálgebra de Lie de simetrias infinitesimais, e esta superálgebra de operadores traz conseqüências extraordinárias para a teoria quantizada. Isto não é mais formal mas concreto. Nisto temos o próprio milagre de supersimetria e a sua beleza tão admirada pelos físicos.