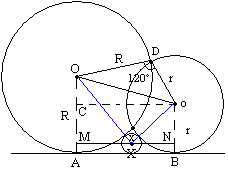
Olá Daniel! --- Daniel Pini <daniel@fnn.net> escreveu: > Duas circunferencias de raios R e r cortam-se > ortogonalmente. Traça-se a tangente externa BC ( B e > C pontos de contato). Calcular o raio da > circunferencia que é tangente externamente às duas > primeiras e tangente a reta BC. > R: Rr/2(R+r+2(Rr)^1/2) Tenho aqui a resolução de uma questão semelhante, mas ao invés de um ângulo de 90° as circunferências se cortam sob um ângulo de 120°. Veja se com essa resolução você consegue fazer a sua que é semelhante. Questão: Duas circunferências de raios R e r cortam-se sob um ângulo de 120º. Traça-se a tangente comum externa AB(A e B pontos de contato). Determine o raio da circunferência que é tangente às duas primeiras e tangente à reta AB. Olhe para a figura 2circ120grau.gif que enviei. A circunferência de centro O tem raio R, a circunferência de centro o (minúsculo) tem raio r e a circunferência tangente às outras duas e à reta AB tem centro X e raio x. O ponto D é um dos pontos de intersecção entre as duas circunferências de centros O e o. Basicamente usaremos o fato de que os segmentos MN e Co são congruentes. Para calcularmos Co precisamos da medida de Oo, que podemos achar usando a lei dos cossenos no triângulo ODo: Oo² = OD² + Do² - 2.OD.Do.(cos 120°) Oo² = R² + r² - 2.R.r.(-1/2) Oo² = R² + r² + Rr Podemos agora calcular o tamanho de Co através do Teorema de Pitágoras no triângulo retângulo OCo: OC² + Co² = Oo² (R - r)² + Co² = R² + r² + Rr Co = raiz(3Rr) Agora podemos achar o comprimento dos segmentos MX e XN pelo teorema de Pitágoras nos triângulos OMX e oNX respectivamente: - No OMX OM² + MX² = OX² (R - x)² + MX² = (R + x)² MX = 2.raiz(Rx) - No oNX oN² + XN² = oX² (r - x)² + XN² = (r + x)² XN = 2.raiz(rx) E agora como MX + XN = MN: MN = Co MX + XN = Do 2.raiz(Rx) + 2.raiz(rx) = raiz(3Rr) 2.raiz(x).[raiz(R) + raiz(r)] = raiz(3Rr) raiz(x) = raiz(3Rr)/2.[raiz(R) + raiz(r)] x = 3Rr/4.[R + 2.raiz(Rr) + r] > Duas circunferencias de raios R e são tangentes > externamente em A. Traça-se a tangente externa BC ( > B e C pontos de contato). Calcular o raio da > circunferencia inscrita no triangulo mixtilíneo > ABC.( o que é um triangulo mixtilineo ABC?) > R: Rr/(R+r+2(Rr)^1/2) O triângulo mistilímeo não tem os lados retos. Olhe para a figura 2circtrimistilineo.gif que enviei. A circunferência de centro O tem raio R, a circunferência de centro o (minúsculo) tem raio r e a circunferência inscrita no triângulo mistilíneo ABC tem centro X e raio x. Basicamente usaremos o fato de que os segmentos MN e Do são congruentes. Podemos calcular o tamanho de Do através do Teorema de Pitágoras no triângulo retângulo ORo: OR² + Do² = Oo² (R - r)² + Do² = (R + r)² Do = 2.raiz(Rr) Agora podemos achar o comprimento dos segmentos MX e XN pelo teorema de Pitágoras nos triângulos OMX e oNX respectivamente: - No OMX OM² + MX² = OX² (R - x)² + MX² = (R + x)² MX = 2.raiz(Rx) - No oNX oN² + XN² = oX² (r - x)² + XN² = (r + x)² XN = 2.raiz(rx) E agora como MX + XN = MN: MN = Do MX + XN = Do 2.raiz(Rx) + 2.raiz(rx) = 2.raiz(Rr) raiz(Rx) + raiz(rx) = raiz(Rr) raiz(x).[raiz(R) + raiz(r)] = raiz(Rr) raiz(x) = raiz(Rr)/[raiz(R) + raiz(r)] x = Rr/[R + 2.raiz(Rr) + r] Abraços, Rafael. _______________________________________________________________________ Yahoo! Mail Mais espaço, mais segurança e gratuito: caixa postal de 6MB, antivírus, proteção contra spam. http://br.mail.yahoo.com/
2circ120grau.gif
2circtrimistilineo.gif