Oi de novo!
Já que ninguém respondeu, estou mandando a minha
resolução que achei horrível! Por isso quero saber se
alguém tem alguma idéia de fazer de uma maneira mais
simples do que isso.
--- Rafael WC <rwcinoto@yahoo.com> wrote:
> Olá Pessoal!
>
> Alguém conseguiria resolver essa pra mim? Não tô
> conseguindo...
>
> AB = 8,AC = 5 e BC = 7 são os lados de um triangulo
> ABC. Inscreve-se neste triangulo uma circunferencia
> e
> traça-se-lhe a tangente paralela ao lado BC, cujos
> pontos de interceção com os lados AB e AC são D e E.
> Calcular a razão ID/IE, sendo I o ponto de contato
> da tangente DE com a circunferencia inscrita no ABC.
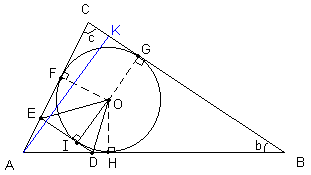
Estou enviando uma figura pra ver se ajuda. Na figura
desenhei o triângulo ABC, inscrevi uma circunferência
de centro O, cujos pontos de tangência aos lados AAC,
BC e AB são respectivamente F, G, H. Depois tracei uma
tangente ao círculo paralela ao lado BC, com ponto de
tangência I e cruzando os lados AB e AC em D e E.
Ainda marquei dois ângulos que iremos precisar, os
ângulos ABC e ACB, que chamei de b e c
respectivamente.
Primeiro vamos calcular a altura do triângulo para
sabermos o seno e cosseno dos ângulos b e c.
Poderíamos usar aqui a lei dos cossenos, mas também
podemos usar a fórmula de Herão para a área, que é
dada por:
área = raiz[p.(p - AB).(p - AC).(p - BC)]
onde p = semi-perímetro
Como AB = 8, AC = 5 e BC = 7, o semi perímetro é:
2p = 8 + 5 + 7
2p = 20
p = 10
E a área será:
área = raiz[p.(p - AB).(p - AC).(p - BC)]
área = raiz[10.(10 - 8).(10 - 5).(10 - 7)]
área = raiz(10.2.5.3)
área = raiz(10.10.3)
área = 10.raiz(3)
Então podemos encontrar a altura AK do triângulo,
relativa ao lado BC por exemplo:
área = base x altura/2
área = BC x AK/2
10.raiz(3) = 7 x AK/2
20.raiz(3) = 7 x AK
AK = 20.raiz(3)/7
Então podemos achar seno, cosseno e tangente de b e c:
sen b = AK/AB
sen b = [20.raiz(3)/7]/8
sen b = [20.raiz(3)/7].(1/8)
sen b = [5.raiz(3)/7].(1/2)
sen b = 5.raiz(3)/14
cos² b + sen² b = 1
cos² b + [5.raiz(3)/14]² = 1
cos² b = 1 - [5.raiz(3)/14]²
cos² b = 1 - 75/196
cos² b = (196 - 75)/196
cos² b = 121/196
cos b = 11/14
tg b = sen b/cos b
tg b = [5.raiz(3)/14]/(11/14)
tg b = 5.raiz(3)/11
sen c = AK/AC
sen c = [20.raiz(3)/7]/5
sen c = [20.raiz(3)/7].(1/5)
sen c = 4.raiz(3)/7
cos² c + sen² c = 1
cos² c + [4.raiz(3)/7]² = 1
cos² c = 1 - [4.raiz(3)/7]²
cos² c = 1 - 48/49
cos² c = (49 - 48)/49
cos² c = 1/49
cos c = 1/7
tg c = sen c/cos c
tg c = [4.raiz(3)/7]/(1/7)
tg c = 4.raiz(3)
Como ED é paralela a BC, quando traçamos os raios OI e
OG até os pontos de tangência, eles formam um segmento
de reta GI, pois os dois raios são perpendiculares a
duas paralelas por um mesmo ponto.
No quadrilátero BGOH, como a soma dos ângulos internos
tem que dar 360°, sabemos que o ângulo GOH = 180° - b.
Como GOI = 180° (pois vimos que é uma reta),
concluímos que HOI = b (pois é suplementar de GOH).
Os triângulos ODH e ODI são congruentes, pois são
triângulos retângulos com dois lados congruentes: o
lado OD comum e os lados OH e OI, que são raios da
circunferência. Assim, o ângulo entre esses lados é
congruente. Isso quer dizer que OD divide o ângulo HOI
(que vale b) em dois ângulos congruentes, de medida
b/2.
Com isso, podemos achar o lado DI em função de OI,
pela tangente de b/2.
Pela fórmula da tangente do arco duplo temos:
tg 2x = 2.tg x/(1 - tg² x)
(tg 2x).(1 - tg² x) = 2.tg x
tg 2x - (tg 2x).(tg² x) = 2.tg x
(tg 2x).(tg² x) - tg 2x + 2.tg x = 0
Fazendo x = b/2, temos:
(tg 2x).(tg² x) - tg 2x + 2.tg x = 0
(tg 2.b/2).(tg² b/2) - tg 2.b/2 + 2.tg b/2 = 0
(tg b).(tg² b/2) - tg b + 2.tg b/2 = 0
Como sabemos o valor de tg b:
[5.raiz(3)/11].(tg² b/2) - 5.raiz(3)/11 + 2.tg b/2 = 0
multiplica tudo por 11,
[5.raiz(3)].(tg² b/2) - 5.raiz(3) + 11.2.tg b/2 = 0
[5.raiz(3)].(tg² b/2) - 5.raiz(3) + 22.tg b/2 = 0
multiplica tudo por raiz(3),
[5.raiz(3)].(tg² b/2) - 5.raiz(3) + 22.tg b/2 = 0
(5.3).(tg² b/2) - 5.3 + 22.raiz(3).tg b/2 = 0
15.(tg² b/2) - 15 + 22.raiz(3).tg b/2 = 0
Mas iso é uma equação do segundo grau. Vamos chamar tg
b/2 de y, para facilitar:
15.(tg² b/2) - 15 + 22.raiz(3).tg b/2 = 0
15.y² - 15 + 22.raiz(3).y = 0
15.y² + 22.raiz(3).y - 15 = 0
E pela fórmula de Báskara encontramos que:
y = [-11.raiz(3) +- 17.raiz(3)]/15
tg b/2 = [-11.raiz(3) +- 14.raiz(3)]/15
Como b/2 é um ângulo do primeiro quadrante, sua
tangente é positiva:
tg b/2 = [-11.raiz(3) + 14.raiz(3)]/15
tg b/2 = 3.raiz(3)/15
tg b/2 = raiz(3)/5
E finalmente encontramos:
tg b/2 = ID/OI
raiz(3)/5 = ID/OI
ID = OI.raiz(3)/5
E agora faremos as mesmas contas para encontrar IE em
função de OI. No quadrilátero CGOF, como a soma dos
ângulos internos tem que dar 360°, sabemos que o
ângulo GOF = 180° - c. Como GOI = 180° (pois vimos que
é uma reta), concluímos que FOI = c (pois é
suplementar de GOF).
Da mesma forma são congruentes os triângulos OEI e
OEF: são retângulos e têm dois lados congruentes, OE
(comum) e OI = OF (raios). Assim, o ângulo entre esses
lados é congruente. Isso quer dizer que OE divide o
ângulo FOI (que vale c) em dois ângulos congruentes,
de medida c/2.
Com isso, podemos achar o lado IE em função de OI,
pela tangente de c/2.
Pela fórmula da tangente do arco duplo, como já vimos,
temos:
(tg 2x).(tg² x) - tg 2x + 2.tg x = 0
Fazendo x = c/2, temos:
(tg 2x).(tg² x) - tg 2x + 2.tg x = 0
(tg 2.c/2).(tg² c/2) - tg 2.c/2 + 2.tg c/2 = 0
(tg c).(tg² c/2) - tg c + 2.tg c/2 = 0
Como sabemos o valor de tg c:
4.raiz(3).(tg² c/2) - 4.raiz(3) + 2.tg c/2 = 0
multiplica tudo por raiz(3),
4.3.(tg² c/2) - 4.3 + 2.raiz(3).tg c/2 = 0
12.(tg² c/2) - 12 + 2.raiz(3).tg c/2 = 0
divide tudo por 2,
6.(tg² c/2) - 6 + raiz(3).tg c/2 = 0
Mas iso é uma equação do segundo grau. Vamos chamar tg
c/2 de y, para facilitar:
6.(tg² c/2) - 6 + raiz(3).tg c/2 = 0
6.y² - 6 + raiz(3).y = 0
6.y² + raiz(3).y - 6 = 0
E pela fórmula de Báskara encontramos que:
y = [-raiz(3) +- 7.raiz(3)]/12
tg c/2 = [-raiz(3) +- 7.raiz(3)]/12
Como c/2 é um ângulo do primeiro quadrante, sua
tangente é positiva:
tg c/2 = [-raiz(3) + 7.raiz(3)]/12
tg c/2 = 6.raiz(3)/12
tg c/2 = raiz(3)/2
E finalmente encontramos:
tg c/2 = IE/OI
raiz(3)/2 = IE/OI
IE = OI.raiz(3)/2
Como o problema pediu a razão ID/IE:
= ID/IE
= [OI.raiz(3)/5]/[OI.raiz(3)/2]
= [OI.raiz(3)/5].[2/OI.raiz(3)]
= [OI/5].[2/OI]
= 2/5
Ufa!
Resposta: ID/IE = 2/5
Abraços,
Rafael
=====
Rafael Werneck Cinoto
ICQ# 107011599
rwcinoto@yahoo.com
rafael.caixa@gov.com.br
matduvidas@yahoo.com.br
http://www.rwcinoto.hpg.com.br/
__________________________________________________
Do You Yahoo!?
LAUNCH - Your Yahoo! Music Experience
http://launch.yahoo.com
circinsctri.gif