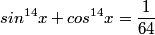Re: [obm-l] equação

["Ralph Teixeira" <ralphct@xxxxxxxxx>]

A ideia fundamental eh notar que a espressao do lado esquerdo eh NO MINIMO 1/64, e isto soh ocorre quando tanx=1. Vejamos como mostrar isto....

 

SOLUCAO I (COM CALCULO II):

 

Considere o problema de minimizar f(x,y)=x^14+y^14 sujeito aa restricao x^2+y^2=1. Use Lagrange, o minimo satisfaz:

 

14x^13=2kx

14y^13=2ky

(ou 2x=2y=0, o que claramente nao serve)

 

Casos:

i) Se x=0, entao y=+-1, entao f=1.

ii) Se y=0, entao x=+-1, entao f=1.

ii) Se x,y<>0 entao 14x^12=14y^12=2k; assim, x=+-y, isto eh, x e y sao ambos +-raiz(2)/2, e f(x,y)=1/64.

 

Assim, o minimo de f(x,y) eh 1/64, que soh ocorre quando x=+-raiz(2)/2 e y=+-raiz(2)/2.

 

Mas x=sint, y=cost satisfaz a restricao! Assim, a expressao do lado esquerdo eh sempre maior ou igual a 1/64, e a igualdade soh ocorre quando sinx=+-raiz2/2 e cosx=+-raiz2/2. Assim, x=kpi/2+pi/4 eh a solucao da sua equacao, k inteiro.

 

SOLUCAO II (COM CALCULO I):

Seja f(x)=(sinx)^14+(cosx)^14. Vamos encontrar o minimo de f(x), digamos, no intervalo [0,2pi], que eh um periodo de f. Note que f`(x)=14sinxcosx((sinx)^12-(cosx)^12). Fazendo f'(x)=0, temos 3 casos:

i) sinx=0 implica f(x)=1

ii) cosx=0 implica f(x)=1

iii) (sinx)^12=(cosx)^12 implica tanx=+-1, entao sinx e cosx sao +- raiz(2)/2, entao f(x)=1/64.

Como f tem de ter um minimo no intervalo fechado [0,2pi], ele eh 1/64, que soh ocorre em x=pi/4,3pi/4, 5pi/4 r 7pi/4. Como f eh periodica, este minimo soh poderah ocorrer nos pontos que correspondem a estes (modulo um periodo). Assim, as unicas solucoes sao x=kpi/2+pi/4, k inteiro.

 

SOLUCAO III (SEM CALCULO, MAS COM MUITO BRACO):

 

i) Pode ser cosx=0? Entao seria sinx=1, o que nao dah certo.

ii) Entao divida tudo por (cosx)^14. Usarei t=(tanx)^2 para economizar bits:

 

(tanx)^14 + 1 = (secx)^14 / 64

64(t^7 + 1) = (t+1)^7

Abre tudo (coragem e binomio de Newton!):

63t^7-7t^6-21t^5-35t^4-35t^3-21t^2-7t+63=0

Note que t=1 eh raiz, e dupla. Elimine-a via Briot-Ruffini (coragem!):

(t-1)^2.(63t^5+119t^4+154t^3+154t^2+119t+63)=0 

 

Soh que o polinomio da direita nao tem raizes positivas nem zero (se tivesse, como eh que aquele bando de numero positivo somado dava zero?). Por outro lado, soh interessam as raizes positivas (lembra que t eh a tangente AO QUADRADO; t negativo nao dah solucao alguma!). Entao soh pode ser t=1, tanx=+-1, e entao x=kpi/2+pi/4 com k inteiro.

 

---///---

 

Tenho certeza que ha outra solucao sem calculo (eu jah vi este problema em algum lugar, acho ateh que caiu em alguma prova quando eu estava na Turma IME/ITA, e eu acho que resolvi do jeito III, e todo mundo ficou embasbacado com a completa **feiura** da minha solucao bracal).

 

Abraco bracal,

                 Ralph

 

On Thu, Nov 1, 2001 at 12:12 AM, Pedro <npc1972@xxxxxxxxx> wrote:

Amigos da lista , me dê um idéia para essa equação:

---