Oi Peter!
Valeu pela dica. Vou tentar fazer com isso pra ver se
fica melhor porque ficou meio comprida a minha
resolução. Veja como acabei resolvendo depois de quase
fundir a cuca:
>Os raios dos circulos inscritos num triangulo
>retangulo ABC e nos dois triangulos ABH e ACH
>determinados pela altura relativa à hipotenusa BC são
>respectivamente r ,r1 e r2. Demonstrar que:
>r² = r1² + r2²
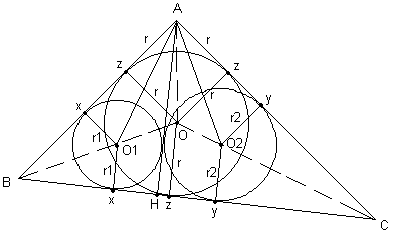
Estou mandando a figura (circinsexinscsemel1.gif) que
não é muito boa, mas é porque são muitos dados. Fiz o
triângulo ABC, retângulo em A, tracei a altura AH e as
3 circunferências em questão:
- a de centro O inscrita em ABC e com raio r;
- a de centro O1 inscrita em ABH e com raio r1;
- a de centro O2 inscrita em ACH e com raio r2.
Na cricunferência de centro O, tracei 3 raios nos
pontos de tangência com os lados AB, AC e BC,
tocando-os nos pontos z. Chamei esses 3 pontos de z,
porque você pode ver que no lado AB o segmento Bz é
congruente ao segmento Bz do lado BC. Assim como o
segmento Cz do lado AC é congruente a Cz do lado BC.
Na circunferência O1 tracei dois raios nos pontos de
tangência dos lados AB e BC, tocando-os nos pontos x.
Chamei os dois de x, porque você pode ver que o
segmento Bx do lado AB é congruente ao segmento Bx do
lado BC.
E por fim, na circunferência O2 tracei dois raios nos
pontos de tangência dos lados AC e BC, tocando-os nos
pontos y. Chamei os dois de y, porque você pode ver
que o segmento Cy do lado AC é congruente ao segmento
Cy do lado BC.
Agora vamos precisar de 4 semelhanças de triângulos.
Primeiro vamos ver que os triângulos AxO1 é semelhante
ao triângulo CyO2, pois os dois triângulos são
retângulos e o ângulo yCO2 mede C/2, assim como o
ângulo xAO1 que é metade do ângulo BAH (AO1 é
bissetriz). E o ângulo BAH é congruente ao ângulo C,
pois BAH é um triângulo retângulo.
Diante dessa semelhança, podemos escrever:
xO1/Ax = yO2/Cy
r1/(AB - Bx) = r2/Cy
E isolando AB:
r1/(AB - Bx) = r2/Cy
r1.Cy = r2.(AB - Bx)
r1.Cy = r2.AB - r2.Bx
r1.Cy + r2.Bx = r2.AB
AB = (r1.Cy + r2.Bx)/r2
Agora vamos ver a semelhança entre os triângulos AyO2
e BxO1. Você sabe que o ângulo xBO1 mede B/2 e como
CHA é retângulo, o ângulo CAH mede B, pois é o
complementar de C. Então, sendo AO2 bissetriz do
ângulo CAH, yAO2 mede B/2 também. SEndo os dois
triângulos retângulos eles são semelhantes. E podemos
escrever:
yO2/Ay = xO1/Bx
r2/(AC - Cy) = r1/Bx
E isolando AC:
r2/(AC - Cy) = r1/Bx
r2.Bx = r1.(AC - Cy)
r2.Bx = r1.AC - r1.Cy
r2.Bx + r1.Cy = r1.AC
AC = (r2.Bx + r1.Cy)/r1
Agora vamos ver a semelhança entre os triângulos CyO2
e CzO. Você pode ver que yO2 e Oz são paralelas então
os dois triângulos são semelhantes. Podemos escrever
as razões:
yO2/Cy = Oz/Cz
r2/Cy = r/Cz
E isolando Cy:
r2/Cy = r/Cz
Cy = r2.Cz/r
E a última semelhança é entre os triângulos BxO1 e
BzO, onde você que xO1 e Oz são paralelas. Então
podemos escrever as razões:
xO1/Bx = Oz/Bz
r1/Bx = r/Bz
E isolando Bx:
r1/Bx = r/Bz
Bx = r1.Bz/r
Agora vamos colocar o valor de Cy e Bx nas equações de
AB e AC:
AB = (r1.Cy + r2.Bx)/r2
AB = (r1.r2.Cz/r + r2.r1.Bz/r)/r2, simplifica r2,
AB = r1.Cz/r + r1.Bz/r, coloca r1/r em evidência,
AB = (r1/r).(Cz + Bz)
AC = (r2.Bx + r1.Cy)/r1
AC = (r2.r1.Bz/r + r1.r2.Cz/r)/r1, simplifica r1,
AC = r2.Bz/r + r2.Cz/r, coloca r2/r em evidência,
AC = (r2/r).(Bz + Cz)
Nas duas fórmulas aparece Bz + Cz, que se você olhar
na base BC da figura, verá que a soma desses dois
segmentos dá exatamente BC, então AC e AB ficam:
AB = (r1/r).(Cz + Bz)
AB = (r1/r).BC
AC = (r2/r).(Bz + Cz)
AC = (r2/r).BC
E como o triângulo ABC é retângulo, podemos escrever o
teorema de Pitágoras e substituir os valores de AB e
AC:
AB² + AC² = BC²
[(r1/r).BC]² + [(r2/r).BC]² = BC²
(r1/r)².BC² + (r2/r)².BC² = BC², simplifica BC²,
(r1/r)² + (r2/r)² = 1
r1²/r² + r2²/r² = 1, tira o mínimo,
r1²/r² + r2²/r² = r²/r²
r1² + r2² = r²
Como queríamos demonstrar.
--- peterdirichlet@zipmail.com.br wrote:
> Caro Rafael,
> agora eu tive uma ideia que pode ajudar.Se voce
> fizer AB=c AC=b, voce consegue
> achar AH,BC,BH e HC em funçao de b e
> c(dica:trigonometria).E,com as ditas
> medidas voce consegue achar os inraios que voce
> quer.E e so substituir e
> comemorar!!!!!
> Peterdirichlet
> PS.:estes tipos de exercicio sao bem comuns em
> olimpiadas!
=====
Rafael Werneck Cinoto
ICQ# 107011599
rwcinoto@yahoo.com
matduvidas@yahoo.com.br
http://www.rwcinoto.hpg.com.br/
__________________________________________________
Do You Yahoo!?
Yahoo! - Official partner of 2002 FIFA World Cup
http://fifaworldcup.yahoo.com
circinsexinscsemel1.gif