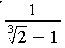Re: Racionalizar

["Alexandre F. Terezan" <aleterezan@xxxxxxxxxxxxx>]

seja k = raiz cúbica de 3

 

seja x^y = x elevado a y

 

Ora, do produto notável temos: a^3 - b^3 = (a - b)(a^2 + ab + b^2)

 

Substituindo a por k e b por 1, vem: k^3 - 1 = (k - 1)(k^2 + k + 1)

 

Mas k^3 - 1 = 2 - 1 = 1

 

Entao, para racionalizarmos a fracao 1/(k - 1), basta multiplicarmos tanto o numerador quanto o numerador por (k^2 + k + 1)...

 

Assim, teremos 1/(k - 1) = k^2 + k + 1

 

Espero ter ajudado.

 

 

----- Original Message -----

From: Davidson Estanislau

To: obm

Sent: Quinta-feira, 29 de Março de 2001 13:43

Subject: Racionalizar

 

    Caros colegas, como faço para racionalizar a seguinte expressão:

 

            

 

    Obrigado.

 

    Davidson