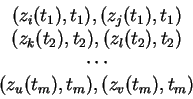Numa variedade M podemos definir transporte paralelo ao longo de
caminhos suaves em M usando uma 1-forma em M com valores matriciais.
A forma ![]() consiste de aplicações lineares dos espaços tangentes
de M nas matrizes
consiste de aplicações lineares dos espaços tangentes
de M nas matrizes
![]() .
Dado um caminho
.
Dado um caminho
![]() ,
temos a equação
,
temos a equação
Seja ![]() a matriz inversivel W(1) (transporte paralelo ao
longo de
a matriz inversivel W(1) (transporte paralelo ao
longo de ![]() ). Se
). Se ![]() e
e ![]() são caminhos em M tais
que
são caminhos em M tais
que
![]() então o caminho
então o caminho
![]() é definido
por
é definido
por ![]() para
para
![]() e
e
![]() para
para
![]() .
Pela unicidade de soluções de EDO's, temos que
.
Pela unicidade de soluções de EDO's, temos que
![]() .
.
Se a 1-forma é plana (flat) então pequenas variações do caminho,
fixando os pontos iniciais e finais não afetam
![]() .
Em outras
palavras,
.
Em outras
palavras,
![]() é invariante por homotopias do caminho
é invariante por homotopias do caminho ![]() que fixam
que fixam ![]() e
e ![]() .
Obtemos assim um homomorfismo
(a monodromia) do grupo fundamental de M nas matrizes
.
Obtemos assim um homomorfismo
(a monodromia) do grupo fundamental de M nas matrizes
![]() inversíveis.
inversíveis.
No artigo [KZ], os físicos Knizhnik e Zamolodchikov definiram uma conexão
plana em Cn pela fórmula
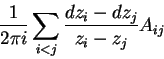
Estas relações e propriedades das formas
![]() garantem que a conexão é plana, ou seja que a 2-forma
de curvatura da conexão é identicamente nula. A verificação deste fato
pode ser encontrada no livro [Ka], capítulo XIX.
garantem que a conexão é plana, ou seja que a 2-forma
de curvatura da conexão é identicamente nula. A verificação deste fato
pode ser encontrada no livro [Ka], capítulo XIX.
Voltando à situação geral, o transporte paralelo ![]() pode ser
visto como limite de produtos de matrizes. Considere primeiro a equação
pode ser
visto como limite de produtos de matrizes. Considere primeiro a equação
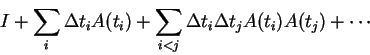
No caso da conexão KZ, a fórmula para o transporte paralelo é
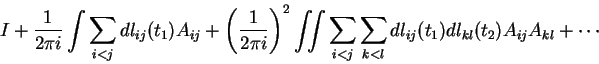
Se b é uma trança, a cada produto
![]() (de
m fatores) corresponde um conjunto de m pares de pontos em b (um
par para cada ti)
(de
m fatores) corresponde um conjunto de m pares de pontos em b (um
par para cada ti)