Ola Rejane,o triangulo DEF tambem eh equilatero (abaixo eu explico), so que, natualmente, maior que o triangulo ABC. Ou seja, eles sao semelhantes, com razao de semelhanca k = 10/100, ou melhor, k = 1/10. Recorde agora que se a razao de semelhanca entre duas figura eh k, entao a razao entre suas areas eh k². Portanto, a razao entre as areas sera:1/100.Por que o triangulo DEF tambem eh equilatero? Repare que os 3 triangulos ADE, EBF e CDF (ops!) sao congruentes entre si, pelo caso LAL. Por exemplo, considerando os triangulos ADE e EBF, temos que o lado BE eh congruente ao AD, o angulo EBF eh congruente ao angulo EAD (ambos de medida igual a 120º) e o lado BF eh congruente a AE, e assim, os lados DE e EF tem a mesma medida. Usando o mesmo raciocinio, voce conclui que o lado DF tem a mesma medida de DE e, consequentemente, de EF, provando queo triangulo DEF eh equilatero e possui os mesmos angulos do triangulo ABC (por isso eles sao semelhantes).Espero que tenha ajudado,Um abraco,Palmerim
Em 15/10/07, Rejane <rejane@rack.com.br> escreveu: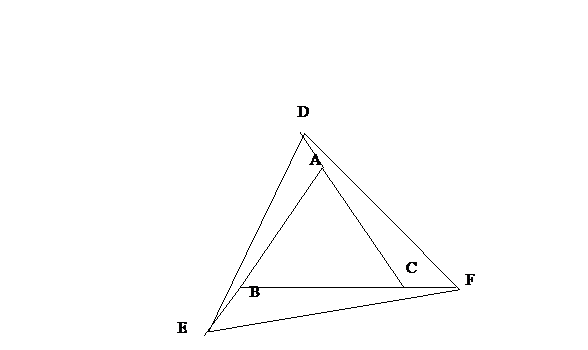
Por Favor, poderiam me ajudar com essa questĂŁo?
Obrigada
Os três lados do triângulo eqüilátero ABC foram prolongados de segmentos AD, BE e CF de
modo que m(AD) = m(BE) = m(CF) e que a medida do segmento AD corresponde a 10% da
medida do lado AC.
Encontrar a razão entre as áreas dos triângulos ABC e DEF.