Re: [obm-l] Um limite meio chato

[Ricardo Bittencourt <ricbit@xxxxxxxxxxxx>]

Claudio Buffara wrote:

>>>>xx=-1e-2:1e-6:1e-2;
> Eu nao conheco o Matlab. Isso quer dizer que voce criou uma "amostra" de
> 20001 vetores (xx,sen(xx)) com xx variando de -1/100 a 1/100 em intervalos
> de 1/10^6?

	Perfeito, isso mesmo.

> Ao fazer a aproximacao de sen(x) por um polinomio de grau m no intervalo
> [-a,a] (a > 0) via minimos quadrados, a partir de uma amostra de n pontos
> igualmente espacados, o que eu acho que acontece eh o seguinte: quando n ->
> infinito, os coeficientes do polinomio tendem aos coeficientes
> correspondentes dos termos de grau <= m da serie de Taylor de sen(x) em
> torno de x = 0. Alias, acho que isso vale pra qualquer funcao infinitamente
> diferenciavel e nao apenas sen(x).

	Concordo contigo!

> Por outro lado, para todo n finito, acho que os coeficientes do polinomio
> soh serao exatamente iguais aos da serie de Taylor da funcao se esta for uma
> funcao polinomial, apesar de se aproximarem destes a medida que n cresce.

	Eu acho que o que acontece é o seguinte:
conforme eu aperto o "a" da tua definição, os coeficientes
chegam mais e mais perto do Taylor, até que quando o
o "a" tende a zero, o polinômio, mesmo de grau finito,
tende aos primeiros termos do Taylor, e isso parece
indiferente se a função original é polinomial ou não.

	Pra mostrar isso fiz um programinha no matlab
que começa com a=100 e vai apertando o resultado. Tracei
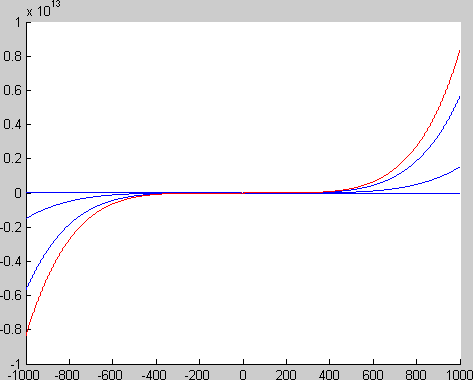
o gráfico dos polinômios resultantes, compare as aproximações
em azul ao polinômio de Taylor truncado, em vermelho.
Todos os polinômios são finitos e de grau 5:

a=100; for i=1:6, x=-a:a*1e-3:a; y=sin(x); a=a*0.5; p=polyfit (x,y,5), 
hold on; t=-1000:1e-2:1000; plot (t,polyval(p,t)); end; plot 
(t,polyval([1/120 0 -1/3 0 1 0],t),'red');

	O lance é que eu lembro de ter feito isso analiticamente,
mas já faz tempo tempo que tive aquela aula, que já não lembro
mais os detalhes.

----------------------------------------------------------------
Ricardo Bittencourt                   http://www.mundobizarro.tk
ricbit@700km.com.br           "tenki ga ii kara sanpo shimashou"
------ União contra o forward - crie suas proprias piadas ------