> 1-Prove que em um triângulo qualquer , suas medianas
> o divide em outros
> 6 triângulos de mesma área.
Olá Rick!
Espero que a figura siga junto...
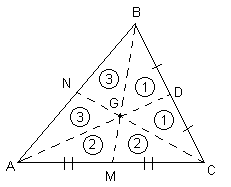
Nessa figura, coloquei os números em alguns triângulos
para identificarmos algumas áreas. Repare que coloquei
o número 1 nos triângulos BDE, BDG e CDG. Você pode
ver que a área dos triângulo BDG e CDG são iguais,
pois os dois triângulos têm a mesma base (BD = DC) e
os dois têm a mesma altura (distância do ponto G até o
lado BC).
Feito isso, também podemos concluir a mesma coisa com
relação aos triângulos AMG e CMG, pelo mesmo motivo,
as bases são iguais e a altura é a mesma. Por isso,
assinalei esses dois triângulos com o nº 2.
E da mesma forma, temos que BGN e AGN têm a mesma
área. E foram assinalados com o nº 3.
Agora repare também que, o triângulo ADB tem a mesma
área do triângulo ADC, pois ambos têm a mesma base e a
mesma altura. Ou seja, cada um tem metade da área do
triângulo ABC. Então vamos escrever essas áreas, em
função dos números. Vou chamar as áreas que estão com
o nº 1 de A1, as com o nº2 de A2 e as outras de A3:
ADB = ADC
BDG + BGN + GNA = DCG + CGM + GMA
A1 + A3 + A3 = A1 + A2 + A2
A3 + A3 = A2 + A2
2.A3 = 2.A2
A3 = A2
Agora podemos também ver que as áreas dos triângulos
BMA e BMC são iguais, pois os dois têm a mesma base
(MC = MA) e a mesma altura (distância do vértice B ao
lado AC). Então escrevendo em função das áreas dos
triângulos menores:
BMA = BMC
MAG + ANG + NGB = GCM + GCD + BGD
A2 + A3 + A3 = A2 + A1 + A1
A3 + A3 = A1 + A1
2.A3 = 2.A1
A3 = A1
Como A1 = A3 e A3 = A2, concluímos que:
A1 = A2 = A3
Então, as 6 áreas em que ficou dividido o triângulo
ABC são todas iguais e equivalem a 1/6 da área total
do triângulo ABC cada uma.
> Um abraço..
> Rick Barbosa====
>
Outro,
Rafael.
=====
Rafael Werneck Cinoto
ICQ# 107011599
rwcinoto@yahoo.com
rafael.caixa@gov.com.br
matduvidas@yahoo.com.br
http://www.rwcinoto.hpg.com.br/
__________________________________________________
Do You Yahoo!?
Yahoo! Games - play chess, backgammon, pool and more
http://games.yahoo.com/
baricentros+baric2.gif