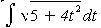Caro Davidson,
Faça t=Sqrt[5] / 2 tan u; dt = Sqrt[5] / 2
sec^2 u du,
Sqrt[5 + 4 t^2] = Sqrt[5 + 5 tan^2 u] = Sqrt[5] sec
u
Então
ISqrt[5+4t^2]dt=Sqrt[5] I sec u Sqrt[5] / 2
sec^2 u du = 5 / 2 Isec^3 du =
= 5/2 ( 1/2 sec u tan u + 1/2 Isec
u du) = 5/4 sec u tan u + 5/4 ( ln |sec u + tan u| ) + c
Lembre-se que tan u = 2t /Sqrt[5], logo a
hipotenusa é Sqrt[5+4t^2] , e sec u =
Sqrt[5+4t^2] / Sqrt[5] .
Agora basta substituir na integral.
Verifique se eu não errei alguma
coisa.
Símbolos: Sqrt[ ] -> raiz
quadrada
I -> integral
A integral de sec^3 eu peguei numa
tabela.
Até logo
----- Original Message -----From: Davidson EstanislauTo: obmSent: Monday, March 26, 2001 11:05 AMSubject: IntegralPor favor, alguém pode me ajudar a resolver essa integral:Agradeço antecipadamenteDavidson