Alguns problemas

Esta página serve para apresentar uma pequena lista de problemas que foram discutidos na reunião para problemas de olimpíadas de matemática do dia 11 de abril de 1999 (na PUC-Rio). As soluções podem ser lidas seguindo os links (mas nem todas estão prontas ainda...).

(1) Escrevemos em um quadro negro os números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Depois disso começa um jogo: a cada vez escolhemos dois números que estejam escritos no quadro, apagamos os dois e escrevemos no quadro a diferença (em módulo, ou seja, o maior menos o menor). Assim, na primeira jogada podemos escolher, digamos, 3 e 7, e ficaríamos com os números 1, 2, 4, 5, 6, 8, 9, 10, 4 no quadro. Repetimos o processo até ficarmos com um único número no quadro. Prove que este último número nunca pode ser 0.

(2) Um quebra-cabeça muito popular é aquele em que temos 15 quadradinhos com os números de 1 a 15 dentro de uma caixinha quadrada, de tal forma que há um espaço vazio do tamanho de um quadradinho. Os quadradinhos podem deslizar
e o jogo original consiste em desarrumar e depois rearrumar os quadradinhos na posição inicial, mostrada na figura abaixo:

[ Figura do quebra-cabeça na posição inicial: [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,*]] ]

Nossa pergunta é: será possível arrumar os números de trás para frente, conforme a figura abaixo?

[ Figura da posição objetivo: [[15,14,13,12],[11,10,9,8],[7,6,5,4],[3,2,1,*]] ]

Ver solução

(3) O cubo de Rubik é outro quebra-cabeça popular. O cubo parece uma pilha cúbica formada por 27=3*3*3 cubinhos que magicamente não desmonta se giramos qualquer uma das seis faces quadradas (formadas por 9 = 3*3 cubinhos cada uma) de um quarto de volta (a ``mágica'' na verdade está na geometria das peças, que não são exatamente cubos, mas não temos como objetivo discutir aqui o funcionamento mecânico do quebra-cabeça). Na posição inicial, cada face é de uma cor. Novamente o jogo original consiste em desarrumar e depois tentar rearrumar o cubo. Nossa pergunta é se é possível girar um cubinho de canto de 1/3 de volta mantendo os outros cubinhos nas suas posições originais. [Falta a figura]

Ver solução

(4a) O resta-um é um jogo para uma pessoa, jogado em um tabuleiro como o mostrado abaixo:

Os pinos vermelhos podem mover-se na horizontal ou vertical (mas não na diagonal), sempre saltando sobre outro pino e caindo em uma casa vazia. O pino por cima do qual se salta é retirado do jogo. A figura abaixo mostra uma posição possível para o tabuleiro após uma jogada:

O objetivo do jogo e deixar um único pino no final (daí o nome do jogo). Demonstre que as únicas posições possíveis para o pino final são as marcadas com um X na figura abaixo:

Ver solução

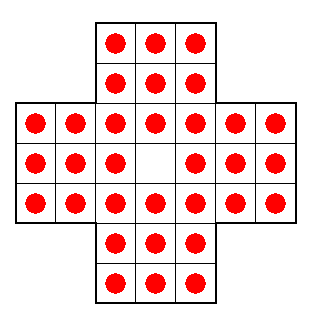
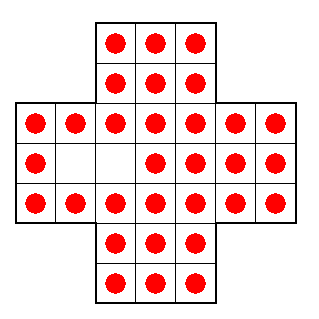
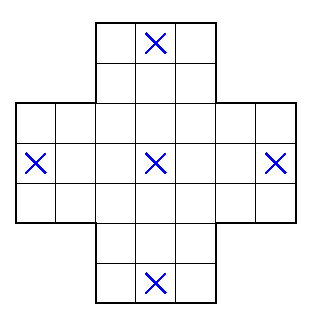
(4b) Com as mesmas regras mas outro tabuleiro, agora quadrado como mostrado na figura, diga se é possivel resolver o quebra-cabeça (isto é, deixar um único pino no final).

[figura de um tabuleiro 8x8 com pinos vermelhos em todos os quadrados, exceto no de posição (3,3)]

Ver solução

(4c) Ainda com as regras de movimento do resta-um, nosso objetivo agora é fazer um pino avançar n espaços além de uma linha reta dada, e a pergunta é: de quantos pinos nós precisamos inicialmente?

Ver solução