Re: [obm-l] Ajuda...

["Rejane" <rejane@xxxxxxxxxxx>]

Fernando,

 

Muito obrigada.

 

Sds

----- Original Message -----

From: Fernando Lukas Miglorancia

To: obm-l@mat.puc-rio.br

Sent: Monday, October 30, 2006 4:04 PM

Subject: Re: [obm-l] Ajuda...

Prezada Rejane,

      Os triângulos ADE e ABC são semelhantes. Digamos que AD=AB.r, DE=BC.r, e assim por diante. Assim, a área de ADE será a área de ABC.(r^2) (r ao quadrado). No entanto, como a área de ADE deve ser igual à do trapézio, a área de ADE será metade da área de ABC, donde se conclui que:

 

          área(ADE)= área(ABC).(r^2)= (1/2). área(ABC)

                                o que implica que (r^2)= (1/2), donde r= raiz de 2 sobre dois,

 

e    AD=AB.r= cinco raiz de dois.

 

    Por favor, me desculpe por estar um pouco bagunçada a minha resolução...

 

Sds.,

 

        Fernando 
 

Em 30/10/06, Rejane <rejane@rack.com.br> escreveu:

Boa tarde, Poderiam me ajudar com esse problema?

 

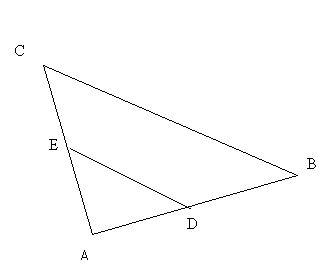
No triangulo ABC queremos traçar o segmento DE paralelo ao lado BC, de modo que a área do trapézio BCDE seja igual à do triângu lo ADE.  Se o lado AB mede 10 cm, a medida AD, em centímetros, é igual a:

a) 2,5

b) 3,5

c) 5

d) 5 raiz de 2

e) 10 raiz de 2