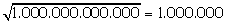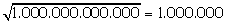[obm-l] Olimpíada do RN

["benedito" <benedito@xxxxxxxxxxxxxx>]

Já estão no site  www.ufrn.br/olimpiada
as provas ( e as soluções) da  XV Olimpíada de Matemática do Rio Grande do
Norte - 2004 (Segunda Etapa).
Alguns dos problemas estão logo a seguir

NÍVEL  I  (5a e 6a Séries)
Problema 4
Sabemos que um trilhão (o mesmo que 1012) é um número quadrado perfeito,
pois .

Qual o menor número natural que é maior que um trilhão e que é um quadrado
perfeito?



Nível II (7a  e 8a  Séries)

Problema 2

Dois operários vão pintar os números dos armários de uma escola. Enquanto o
mais velho dos pintores pinta cinco algarismos, o mais novo só consegue
pintar quatro. O pintor mais novo começou pelos números mais baixos  1, 2,
3, ..... O pintor mais velho começou pelo último armário e foi pintando em
ordem decrescente, até encontrar seu colega. No final, duas coincidências se
verificaram:

  a.. Os dois pintores acabaram ao mesmo tempo, cada um em seu armário.
  b.. Os dois pintaram o mesmo número de armários.
Quantos armários há na escola?

  Nível III (Ensino Médio)

Problema 2
Um matemático excêntrico escreve um livro, numerando as páginas de  2  até
400, e com  a recomendação de que a leitura deve ser feita na seguinte
ordem. Identifica-se a última página não lida (no início da leitura é a
página de número 400) e a seguir lê-se (na ordem usual) todas as páginas
numeradas com números que não são relativamente primo com ela e que não
tenham sido lidas anteriormente. Repete-se este procedimento até que se
completa a leitura do livro. Deste modo, a ordem da leitura seria  2, 4, 5,
...., 400, 3, 7, 9, ...., 399, .....
Qual é a última página a ser lida?



Problema 3
Numa cidade, a Avenida Jerimum tem dez quadras de comprimento. Em cada
quadra moram um rapaz e uma garota. Eles querem fazer amigos de tal modo que
cada rapaz seja amigo de exatamente uma garota e vice-versa. Ninguém quer um
amigo(a) morando mais de uma quadra de distância da sua, mas eles podem
morar na mesmo quadra.

Nestas condições, quantos pares   (rapaz, garota)   existem?



Problema 4
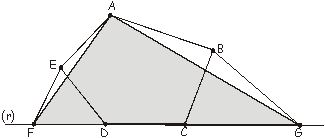
Na figura abaixo, ABCDE  é um pentágono cujo lado DC está sobre a reta (r).
Traçamos EF//AD  e  BG//AC.

Verifique que o triângulo  AGF  e  o pentágono ABCDE  têm a mesma área.




-- 
Esta mensagem foi verificada pelo sistema de anti-virus e
 acredita-se estar livre de perigo.