O invariante

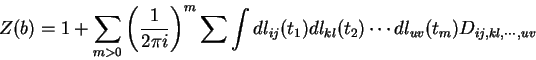
Seja

$$Z(b)=1+\sum _{m>0} \left(\frac {1}{2 \pi i}\right)^m \sum \in... ...ij}(t_1) dl_{kl}(t_2) \cdots dl_{uv}(t_m) D_{ij,kl, \cdots ,uv}$$

onde os limites de integração são $1>t_1>t_2> \cdots >t_m>0$ e a segunda soma $\sum$ é sobre todo $i<j , k<l , \cdots ,u<v$ e $D_{ij,kl, \cdots ,uv} \in A_m(b)$ é o m-diagrama em b que consiste dos pares $(z_i(t_1),t_1),(z_j(t_1),t_1), \cdots , (z_u(t_m),t_m),(z_v(t_m),t_m).$

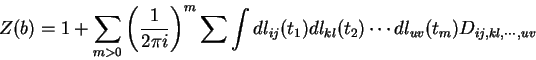
Esta fórmula é a fórmula antiga com $D_{ij,kl, \cdots ,uv}$ no lugar do produto $A_{ij}A_{kl} \cdots A_{uv}$. As relações entre os A_ij correspondem às relações 4T. Por exemplo, temos a relação 4T

D_ij,jk - D_jk,ij + D_ij,ik - D_ik,ij = 0

que corresponde à relação [A_ij, A_jk] = [A_ik, A_ij]. Também D_ij,kl é D_kl,ij são equivalentes como diagramas se i, j, k, l são distintos, o que corresponde à relação [A_ij,A_kl] = 0.

Z(b) tem propriedades análogas às do transporte paralelo respeito à conexão KZ:

• Se b e c são tranças equivalentes então Z(b) = Z(c)
• Z(b₁ b₂) = Z(b₁)Z(b₂).

Para simplificar a discussão só consideraremos tranças cujos fechos são nós. Para tais tranças, temos a aplicação $p:A(b) \to A(S^1)$

Teorema: pZ(b₁ b₂)=pZ(b₂ b₁)

Demonstração: pZ(b₁ b₂)=p(Z(b₁)Z(b₂))=p(Z(b₂)Z(b₁))=pZ(b₁ b₂).          $\blacksquare$

Então pZ satisfaz a primeira condição de Markov. A segunda condição, porém, não é satisfeita. Por exemplo, calculemos pZ para a 2-trança $\sigma_1$. O resultado é

$$pZ(\sigma_1) = 1 + \sum _{m>0} \frac{1}{2^m m!} \bigcirc _m$$

onde $\bigcirc _m \in A_m(S^1)$ é o m-diagrama $a_1a_2 \cdots a_m a_1a_2 \cdots a_m$ em S¹. Para $\sigma_1$ temos que $z_1 - z_2 = -e^{\pi i t}$. Então o coeficiente de $\bigcirc _m$ é

$$\left(\frac{1}{2 \pi i}\right) ^m \int \left(\pi i \right)^m dt_1 \cdots dt_m,$$

ou seja 2^-m vezes o volume 1/m! do m-simplexo aberto $1 > t_1 > \cdots > t_m > 0$. A fórmula para $\sigma_1^{-1}$ é

$$pZ(\sigma _1 ^{-1}) = 1 + \sum_{m>0} \frac {1}{2^m m!} \left(-1 \right) ^m \bigcirc _m$$

.

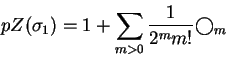
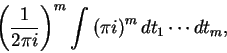
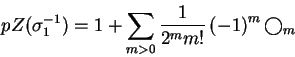
A idéia de Picken é de passar ao quociente pelas relações $pZ(\sigma _1 ^{\pm 1}) = 1$ para garantir a segunda condição de Markov. Sejam então r₊ e r_- os elementos de A dados por $r_{\pm} = pZ( \sigma _1 ^{\pm 1}) - 1$ e seja $\bar{A}$ o quociente de A pelo ideal r₊ A + r_- A gerado por r₊ e r_- e seja $\bar{p}$ a composta de p com a aplicação quociente $A \to \bar{A}$.

O resultado principal de [P] (cuja demonstração será omitida) é que $\bar{p} Z (b)$ satisfaz a segunda condição de Markov e, portanto, define um invariante de nós.

Como exemplo de como calcular com o invariante, esboçaremos uma demonstração de que o invariante distingue entre o trevo e a sua reflexão num plano. O trevo é o fecho da 2-trança $\sigma_1 ^3$ dada pelas duas funções $3/2 \pm e^{3 \pi i t}/2$, enquanto a sua reflexão $\sigma _1 ^{-3}$ é dada por $3/2 \pm e^{-3 \pi i t}/2$. Como no caso de $\sigma_1$, temos que

$$pZ( \sigma_1 ^3 ) = 1 + \frac{3}{2} \bigcirc _1 + \frac{9}{8} \bigcirc _2 + \frac{9}{16} \bigcirc_3 + \cdots$$

que, depois de uma pequena conta, é igual a

$$1 + 6r_+ + 3r_- + \frac{1}{2} \bigcirc _3 + \cdots$$

onde os pontinhos representam termos em A_m para m>3.

O trevo refletido é o fecho da 2-trança $\sigma _1 ^{-3}$ e temos

$$pZ( \sigma_1 ^ {-3}) = 1 + 3r_+ + 6r_- - \frac{1}{2} \bigcirc_3 + \cdots.$$

Subtraindo, temos que

$$pZ(\sigma_1 ^3) - pZ(\sigma_1 ^{-3}) = 3r_+ -3r_- + \bigcirc_3 + \cdots$$

.

Examinando as relações 4T em A₃ não é dificil verificar que nenhuma soma da forma $\bigcirc_3 + \cdots$ pode pertencer ao ideal r₊A + r_-A. Então $\bar{p}Z( \sigma_1 ^3 ) \neq \bar{p}Z( \sigma _1 ^{-3})$, ou seja o valor do invariante é diferente para o trevo e a sua reflexão.