Sejam
![]() .
Dizemos que a é congruente a b módulo n,
e escrevemos
.
Dizemos que a é congruente a b módulo n,
e escrevemos
![]() ,
se n|b - a.
Como a congruência módulo 0 é a igualdade
e quaisquer inteiros são côngruos módulo 1,
em geral estamos interessados em n > 1.
,
se n|b - a.
Como a congruência módulo 0 é a igualdade
e quaisquer inteiros são côngruos módulo 1,
em geral estamos interessados em n > 1.
Proposição 1.7:
Para quaisquer
![]() temos:
temos:
Dem:
Para o item (a) basta observar que
n | a - a = 0.
Em (b), se n | b - a então
n | a - b = -(b-a).
Em (c), se n | b - a e n | c - b então
n | c - a = (c - b) + (b - a).
Em (d), se
n | a' - a e
n | b' - b então
n | (a' + b') - (a + b) = (a' - a) + (b' - b).
Em (e), se
n | a' - a então
n | (-a') - (-a) = -(a' - a).
Em (f), se
n | a' - a e
n | b' - b então
n | a'b' - ab = a'(b' - b) + b(a' - a).
![]()
Os itens (a), (b) e (c) da proposição acima dizem, nesta ordem, que a relação
![]() (``ser côngruo módulo n'')
é uma relação reflexiva, simétrica e transitiva.
Relações satisfazendo estas três propriedades são chamadas
relações de equivalência.
Dada uma relação de equivalência
(``ser côngruo módulo n'')
é uma relação reflexiva, simétrica e transitiva.
Relações satisfazendo estas três propriedades são chamadas
relações de equivalência.
Dada uma relação de equivalência ![]() sobre um conjunto Xe um elemento
sobre um conjunto Xe um elemento ![]() definimos a classe de equivalência
definimos a classe de equivalência
![]() de x como
de x como
Aplicando esta construção geral ao nosso caso, definimos o quociente
![]() ,
chamado por simplicidade de notação de
,
chamado por simplicidade de notação de
![]() ,
,
![]() ou às vezes
ou às vezes
![]() .
Dado
.
Dado
![]() ,
a definição de
,
a definição de
![]() como um subconjunto de
como um subconjunto de
![]() raramente será importante: o importante é sabermos que
raramente será importante: o importante é sabermos que
![]() se e somente se
se e somente se
![]() .
Se n > 0, a divisão euclidiana diz que todo inteiro a é côngruo a um único
inteiro a' com
.
Se n > 0, a divisão euclidiana diz que todo inteiro a é côngruo a um único
inteiro a' com
![]() ;
podemos reescrever este fato na nosso
nova linguagem como
;
podemos reescrever este fato na nosso
nova linguagem como
Os itens (d), (e) e (f) da proposição dizem que as operações de soma,
diferença e produto são compatíveis com a relação de congruência.
É esta propriedade que torna congruências tão úteis,
nos possibilitando fazer contas módulo n.
Podemos por exemplo escrever
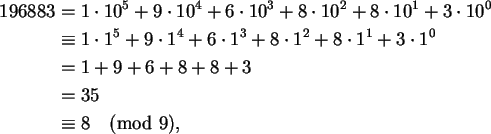
já que
![]() (mostrando assim porque funciona o conhecido critério de divisibilidade por 9).
Uma formulação mais abstrata da mesma idéia é dizer que as operações
+ e
(mostrando assim porque funciona o conhecido critério de divisibilidade por 9).
Uma formulação mais abstrata da mesma idéia é dizer que as operações
+ e ![]() passam ao quociente, i.e., que podemos definir
passam ao quociente, i.e., que podemos definir
Proposição 1.8:
Sejam
![]() , n > 0.
Então existe
, n > 0.
Então existe
![]() com
com
![]() se e somente se (a,n) = 1.
se e somente se (a,n) = 1.
Dem:
Se
![]() temos
nk = 1 - ab para algum k,
donde
(a,n) | ab + nk = 1 e (a,n) = 1.
Se (a,n) = 1 temos
ax + ny = 1 para certos inteiros x e y,
donde
temos
nk = 1 - ab para algum k,
donde
(a,n) | ab + nk = 1 e (a,n) = 1.
Se (a,n) = 1 temos
ax + ny = 1 para certos inteiros x e y,
donde
![]() .
.
![]()
Dizemos portanto que a é invertível
1.1
módulo n quando (a,n) = 1e chamamos b com
![]() de inverso
de a módulo n.
O inverso é sempre único módulo n:
se
de inverso
de a módulo n.
O inverso é sempre único módulo n:
se
![]() temos
temos
![]() .
.
Corolário 1.9:
Se (a,n) = 1 e
![]() então
então
![]() .
.
Dem:
Basta escrever
![]() onde c é o inverso de a módulo n.
onde c é o inverso de a módulo n.
![]()
Definimos
![]() por
por
Teorema 1.10: (Teorema Chinês dos restos)
Se
(m, n) = 1 então
![]()
é uma bijeção.
Além disso, a imagem por f de
![]() é
é
![]() .
.
Note que cada
![]() na definição de fé tomado em relação a um módulo diferente.
A função está bem definida pois
na definição de fé tomado em relação a um módulo diferente.
A função está bem definida pois
![]() determina
determina ![]() e
e ![]() .
.
Dem:
Como
![]() e
e
![]() têm mn elementos cada,
para provar que f é bijetiva basta verificar que f é injetiva.
E, de fato, se
têm mn elementos cada,
para provar que f é bijetiva basta verificar que f é injetiva.
E, de fato, se
![]() e
e
![]() então
m | (a - a') e
n | (a - a'),
donde
mn | (a - a') e
então
m | (a - a') e
n | (a - a'),
donde
mn | (a - a') e
![]() .
A imagem de
.
A imagem de
![]() é
é
![]() pois
(a,mn) = 1 se e somente se
(a,m) = (a,n) = 1.
pois
(a,mn) = 1 se e somente se
(a,m) = (a,n) = 1.
![]()
Dados inteiros
![]() ,
dizemos que estes inteiros
são primos entre si se
(mi,mj) = 1 para quaiquer
,
dizemos que estes inteiros
são primos entre si se
(mi,mj) = 1 para quaiquer ![]() .
.
Corolário 1.11:
Se
![]() são inteiros primos entre si. Então
são inteiros primos entre si. Então
![]()
é uma bijeção.
Dem:
Basta aplicar o teorema anterior r vezes.
![]()
A aplicação mais comum deste teorema é para garantir que existe
a com
![]() onde ai são inteiros dados quaisquer.
onde ai são inteiros dados quaisquer.