Fórmulas para primos e testes de primalidade

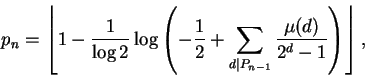
Mencionamos na introdução deste capítulo que não se conhece nenhuma fórmula simples para gerar primos arbitrariamente grandes. Uma palavra imprecisa mas importante nesta frase é ``simples''. Existem fórmulas que geram números primos, mas que são tão complicadas que não ajudam muito nem a gerar números primos explicitamente nem a responder perguntas teóricas sobre a distribuição dos primos. Um exemplo de fórmula para p_n, o n-ésimo primo, é

$$p_n = \left\lfloor{ 1 - \frac{1}{\log 2} \log\left( {-\frac{1... ...\vert P_{n-1}}\frac{\mu(d)}{2^d - 1}} \right) } \right\rfloor,$$

onde $P_{n-1} = p_1 p_2 \cdots p_{n-1}$; deixamos a demonstração a cargo do leitor. Outra fórmula é

$$p_n = \lfloor 10^{2^n} c \rfloor - 10^{2^{n-1}} \lfloor 10^{2^{n-1}} c \rfloor,$$

onde

$$c = \sum_{n = 1}^\infty \frac{p_n}{10^{2^n}} = 0.0203000500000007\ldots .$$

A inutilidade desta última fórmula vem do fato que para calcular cdevemos encontrar todos os primos; a fórmula se tornaria mais interessante se existisse outra interpretação para o número real c, o que parece muito improvável. Por outro lado, exite um número real a > 1tal que $\lfloor a^{3^n} \rfloor$ é sempre primo.

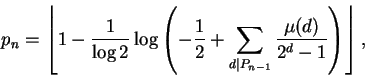
Um tipo de fórmula para primos, de certa forma mais intrigante, são polinômios de coeficientes inteiros em S variáveis com a seguinte propriedade quase mágica: a interseção da imagem de ${\mathbb{N} }^S$ com ${\mathbb{N} }$é exatamente o conjunto dos números primos. Note que se tomarmos um ponto de ${\mathbb{N} }^S$ ``ao acaso'', o valor do polinômio neste ponto quase certamente será negativo; assim, é difícil usar o polinômio para gerar primos. A título de curiosidade, vejamos um exemplo de polinômio com estas propriedades; aqui N = 26, o valor do polinômio é P, as variáveis chamam-se $a, b, \ldots, z$ e $A, B, \ldots, N$são expressões auxiliares:
$$\begin{align}P &= (k+2)(1 - A^2 - B^2 - C^2 - \cdots - N^2), \notag\\ A &= wz +... ...p - 2) - x,\notag\\ N &= z + pl(a-p) + t(2ap - p^2 - 1) - pm.\notag \end{align}$$
Algumas observações simples: a única forma de P ser positivo é se $A = B = \cdots = N = 0$; neste caso seu valor será k+2. Vemos assim que para produzir um número primo P com este polinômio devemos antes de mais nada tomar k = P-2. As expressões auxiliares viram equações: como A = 0 temos q = wz + h + j. Assim, dado k para o qual k+2 é primo, precisamos procurar valores para as outras letras que satisfaçam estas equações. Estes valores de certa forma encodificam uma demonstração de que P = k+2 é primo.

Uma questão relacionada com a de gerar números primos é a de testar se um determinado número é primo. Existe um algoritmo bastante simples para testar se qualquer inteiro positivo n é primo: calcule o resto da divisão de npor cada inteiro m com $2 \le m \le \sqrt{n}$. Se o resto for 0 em algum caso então n é composto e encontramos um divisor; se isto nunca ocorrer, n é primo. O inconveniente deste algoritmo é que ele é muito lento: mesmo para um inteiro de 200 algarismos, teríamos que fazer aproximadamente 10¹⁰⁰ divisões o que não só está fora do alcance da tecnologia atual mas fora do alcance de qualquer tecnologia plausível de acordo com o que se conhece de física ^3.1.

Alguns teoremas de teoria dos números podem ser usados para testar a primalidade de um inteiro positivo n. Pelo teorema de Wilson, por exemplo, podemos testar a primalidade de n calculando $(n-1)! \bmod n$; infelizmente, esta conta parece ser tão difícil de efetuar quanto a busca de divisores pelo algoritmo anterior. Observe que dizemos apenas que a conta parece difícil: não está excluída a possibilidade de alguém inventar um algoritmo rápido para calcular $(n-1)! \bmod n$.

Uma idéia mais bem sucedida é a de usar o pequeno teorema de Fermat: tomamos a, 1 < a < n, e calculamos $a^{n-1} \bmod n$. Se n for primo teremos $a^{n-1} \equiv 1 \pmod n$; qualquer outro resultado indica que n é composto mesmo sem termos encontrado um fator de n. Observe que para calcular $a^{n-1} \bmod n$ não precisamos calcular $a \cdot a \cdots a$, n - 1 vezes. Podemos fazer esta conta com menos de $4 \log_2 n$ operações envolvendo inteiros menores do que n²: se $n - 1 = \sum_{0 \le i < N} b_i 2^i$, $N = \lfloor \log_2 (n-1) \rfloor$, então definimos

$$p_k = a^{\sum_{0 \le i < k} b_{N-k+i} 2^i} \bmod n$$

e temos p₀ = 1, $p_N = a^{n-1} \bmod n$, e podemos calcular p_k+1 a partir de p_k com uma operação de elevar ao quadrado, tomar o resto da divisão por n, possivelmente multiplicar por a e novamente de tomar o resto da divisão por n.

Se $a^{n-1} \equiv 1 \pmod n$, por outro lado, não demonstramos que n é primo; se n for composto satisfazendo $a^{n-1} \equiv 1 \pmod n$dizemos que n é um pseudoprimo na base a. Pseudoprimos existem mas são raros (ver (Cipolla]): o menor pseudoprimo na base 2 é $341 = 11 \cdot 31$e existem apenas 21.853 pseudoprimos na base 2 menores do que $2,5 \cdot 10^{10}$ (contra 1.091.987.405 primos). Pomerance (melhorando um resultado anterior de Erdös) provou que se $P\pi_a(x)$ é o número de pseudoprimos até x na base a temos

$$P\pi_a(x) \le x \cdot e^{ - \frac{\log x \log \log \log x}{2 \log \log x}}$$

para x suficientemente grande. A proposição abaixo exibe uma família infinita de pseudoprimos na base a (para qualquer a > 1 dado); assim a simples verificação $a^{n-1} \equiv 1 \pmod n$não demonstra a primalidade de n.

Proposição 3.1: Seja a > 1 e p primo, p > 2. Então

$$n = \frac{a^{2p} - 1}{a^2 - 1} = \frac{a^p - 1}{a - 1} \cdot \frac{a^p + 1}{a + 1}$$

é um pseudoprimo na base a.

Dem: Pelo pequeno Teorema de Fermat,

$$\frac{a^p - 1}{a - 1} \equiv \frac{a^p + 1}{a + 1} \equiv 1 \pmod p$$

e verifica-se facilmente que estes números são ímpares, donde $n \equiv 1 \pmod {2p}$, ou n = 2kp + 1 para k inteiro. Assim, como $a^{2p} \equiv 1 \pmod n$ temos $a^n = a^{2kp + 1} = (a^{2p})^k \cdot a \equiv a \pmod n$.          $\blacksquare$

Uma idéia natural é a de testar vários valores de a. Claramente, se (a,n) > 1, teremos $a^{n-1} \not\equiv 1 \pmod n$; entretanto, se n for um produto de uns poucos primos grandes os valores de a para os quais (a,n) > 1 são raros e se formos obrigados a encontrar um tal valor de ateremos feito muito pouco progresso em relação aos primeiros algoritmos. Aliás, uma vez encontrado a com (a,n) > 1 é fácil encontrar (a,n) pelo algoritmo de Euclides, o que nos dá uma fatoração (parcial) de n. É um fato interessante que existam alguns raros números compostos n, chamados números de Carmichael, com a propriedade que se 0 < a < n e (a,n) = 1então $a^{n-1} \equiv 1 \pmod n$. Foi até demonstrado recentemente por Alford, Granville e Pomerance que se CN(x) é o número de números de Carmichael menores do que x então

$$CN(x) \ge x^{2/7}$$

para x suficientemente grande, o que implica na existência de infinitos números de Carmichael. Há apenas 2163 números de Carmichael menores do que $2,5 \cdot 10^{10}$e os primeiros são 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633, 62745, 63973 e 75361 ^3.2.

Podemos refinar o conceito de pseudoprimo para definir pseudoprimos fortes na base a. Para definir quando n é um pseudoprimo forte na base ainicialmente escrevemos $n-1 = 2^k \cdot b$, com b ímpar. Se n > 2 é primo deve existir um menor valor de jpara o qual $(a^b)^{2^j} \equiv 1 \pmod n$(observe que por Fermat $(a^b)^{2^k} \equiv 1 \pmod n$). Se j = 0 isto significa que $a^b \equiv 1 \pmod n$; caso contrário temos $(a^b)^{2^{j-1}} \equiv -1 \pmod n$já que -1 é o único valor de x diferente de 1 (módulo n) para o qual $x^2 \equiv 1 \pmod p$. Assim, dizemos que n composto ímpar é um pseudoprimo forte na base ase ou $a^b \equiv 1 \pmod n$ ou existe j' < k com $(a^b)^{2^{j'}} \equiv -1 \pmod n$. Claramente todo pseudoprimo forte na base aé um pseudoprimo na base a mas pseudoprimos fortes são mais raros do que pseudoprimos.

Observe que se n for pseudoprimo base a mas não pseudoprimo forte base a, então o teste acima não apenas demonstra que n é composto mas produz uma fatoração parcial de n. De fato, seja c = (a^b)^2j-1; temos $c - 1 \not\equiv 0 \pmod n$, $c + 1 \not\equiv 0 \pmod n$ mas $(c - 1)(c + 1) = c^2 - 1 \equiv 0 \pmod n$. Assim, n = (n,c-1)(n,c+1).

Existem infinitos pseudoprimos fortes em qualquer base a > 1: Pomerance provou que, se $SP\pi_a(x)$ é o número de pseudoprimos fortes na base a menores ou iguais a x então

$$SP\pi_a(x) \ge e^{(\log x)^{5/4}}$$

para todo x suficientemente grande (ver [Pomerance]). Não existem ``números de Carmichael fortes'': para todo número composto ímpar n existe 0 < a < ncom (a,n) = 1 e tal que n não é um pseudoprimo forte na base a. Melhor ainda, os valores de a que servem de testemunha para a não-primalidade de n são sempre relativamente freqüentes, como vemos na proposição abaixo.

Proposição 3.2: Seja n > 1, n composto ímpar. Então o número de inteiros a, 0 < a < n, para os quais n é um pseudoprimo na base aé menor do que n/2.

Dem: Seja $n = p_1^{e_1} \ldots p_m^{e_m}$ a fatoração completa de n. Pelo Teorema chinês dos restos e pela existência de raízes primitivas módulo p_i^e_i, podemos escrever $G = ({\mathbb{Z} }/(n))^\ast = {\mathbb{Z} }/\varphi(p_1^{e_1}) \oplus \cdots \oplus {\mathbb{Z} }/\varphi(p_m^{e_m})$. Se escrevamos $\varphi(p_i^{e_i}) = 2^{k_i} \cdot b_i$, com b_i ímpar, podemos também escrever $G = G_2 \oplus G_o$, onde $G_2 = {\mathbb{Z} }/(2^{k_1}) \oplus \cdots \oplus {\mathbb{Z} }/(2^{k_m})$e G_o tem ordem ímpar. Não é difícil ver que n é um pseudoprimo forte na base ase e somente se a ordem das componentes de a^b em cada componente ${\mathbb{Z} }/(2^{k_i})$ é a mesma (onde $n-1 = 2^k \cdot b$ com b ímpar). Mas dada uma ordem (digamos, a ordem de a^b em ${\mathbb{Z} }/(2^{k_1})$) o número de elementos de ${\mathbb{Z} }/(2^{k_2})$ com aquela ordem prescrita é no máximo a metade da ordem do grupo.          $\blacksquare$

Na verdade pode-se demonstrar um resultado mais forte (quase certamente o melhor possível):

Teorema 3.3: Seja n > 1, n composto ímpar. Então o número de inteiros a, 0 < a < n, para os quais n é um pseudoprimo na base aé menor do que n/4.

A demonstração deste teorema será omitida; o leitor pode considerar isto como um exercício. O caso em que n tem três ou mais fatores primos distintos pode ser tratado como na demonstração da proposição.

O teorema acima serve de base para os testes de primalidade probabilísticos. Dado n, tomamos N valores de a ao acaso no intervalo 1 < a < ne verificamos para cada a se n passa no teste de primalidade na base a. Se n for ímpar composto, a probabilidade de que um dado aacuse a não-primalidade de a é maior do que 3/4 (pelo teorema); assim, a probabilidade de que n escape a N testes é menor do que 4^-N. Mesmo para valores moderados de N podemos dizer, se n passar no teste, que n é provavelmente primo. Este tipo de teste é extremamente útil em aplicações (como em criptografia) onde é importante criar primos relativamente grandes mas não existe a preocupação com demonstrações ou com perfeição absoluta. Nosso ponto de vista neste livro, entretanto, é o de um matemático: queremos não apenas um teste probabilístico mas uma demonstração da primalidade de n. Para isto nosso teste não parece tão bom: para demonstrarmos que n é primo ainda somos obrigados a testar aproximadamente n/4 valores de a, o que é lento demais.

Existe uma variação do conceito de pseudoprimalidade forte. Suponhamos que $n - 1 = p^k \cdot b$, $p \nmid b$. Seja a um inteiro, 0 < a < n. O pequeno teorema de Fermat diz que se n é primo devemos ter $(a^b)^{p^k} \equiv 1 \pmod n$. Suponhamos que isto ocorra: nosso teste refinado consiste em considerar o último termo não côngruo a 1 módulo n da seqüência $a^b, (a^b)^p, (a^b)^{p^2}, \ldots, (a^b)^{p^k}$: chamemos este termo de c(se ocorrer $a^b \equiv 1 \pmod n$ não podemos aplicar o teste). Temos claramente $c^p - 1 = (c^{p-1} + \cdots + c + 1)(c - 1) \equiv 0 \pmod n$e $c - 1 \not\equiv 0 \pmod n$; se n for primo devemos obrigatoriamente ter $c^{p-1} + \cdots + c + 1 \equiv 0 \pmod n$. Em outras palavras, se $c^{p-1} + \cdots + c + 1 \not\equiv 0 \pmod n$sabemos que n é composto. Assim como no caso de pseudoprimos fortes, se n for pseudoprimo na base a mas falhar este teste para algum primo pacabamos de obter uma fatoração para n: $n = (n,c-1)(n,c^{p-1} + \cdots + c + 1)$.

Já enunciamos a hipótese de Riemann no capítulo 1. Existe uma generalização importante da hipótese de Riemann, chamada hipótese de Riemann generalizada. Uma descrição precisa do enunciado da hipótese de Riemann generalizada está fora dos nossos objetivos mas ela tem conseqüências muito importantes para testes de primalidade.

Teorema 3.4: (Teste de Miller) Se a hipótese de Riemann generalizada é verdadeira então para todo n ímpar composto existe $a < 2(\log n)^2$tal que nnão é um pseudoprimo forte na base a.

Não daremos a demonstração do teorema acima; o leitor interessado deve consultar [Bach].

Uma demonstração da hipótese de Riemann generalizada implicaria assim na existência de um teste de primalidade rápido e geral: não é difícil verificar que o tempo necessário para verificar primalidade de n pelo teste de Miller é limitado superiormente por um polinômio em $\log n$. Existe um outro algoritmo, bem mais sofisticado, devido a Adleman, Pomerance e Rumely, que demonstra (sem a necessidade de invocar conjecturas como a hipótese de Riemann) a primalidade de um primo n em um tempo limitado por $(\log n)^{c\log \log \log n}$ para uma certa constante positiva c.

Existem muitos valores de n para os quais é possível demonstrar primalidade em um tempo muito menor do que pelo teste de Miller. Veremos duas grandes classes de testes especiais: quando conhecemos uma fatoração (pelo menos parcial) para n-1 e quando conhecemos uma fatoração (também pelo menos parcial) para n+1.