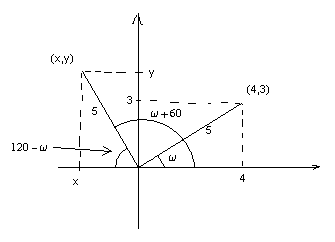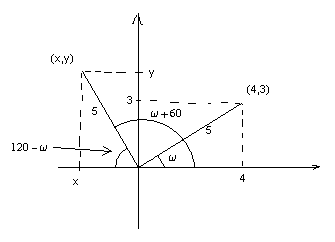Re: [obm-l] Geometria Anlítica

[Claudio Freitas <claudio_exatas@xxxxxxxxxxxx>]

Sugestão de Resolução:
Supondo que se queira fazer uma rotação do ponto em 60º no sentido 
anti-horário em relação à origem...
Representando o ponto (4,3) pelo número complexo 4 + 3i, podemos fazer a 
rotação desejada multiplicando-o pelo complexo 1(cos(60º) + i.sen(60º)).
Então temos:  w = (4 + 3i).(raiz(3)/2  +  i/2)   =   2.raiz(3) + 2i + 
3.raiz(3).i/2 - 3/2   =   [2.raiz(3) - 3/2] + i.[2 + 3.raiz(3)/2]
Logo o ponto procurado é:  (2.raiz(3) - 3/2 , 2 + 3.raiz(3)/2)





Outro jeito de fazer:

Pelo T. de Pitágoras, a distância do ponto P(4,3) até a origem (0,0) é 
5. Chamemos o ângulo que P faz com o eixo x de w.

Pela figura, temos:

sen(120 - w) = y/5
sen(120).cos(w) - sen(w).cos(120) = y/5   (I)

cos(120 - w) = x/5
cos(120).cos(w) + sen(120).sen(w) = x/5   (II)

sen(w) = 3/5
cos(w) = 4/5

Substituindo sen(w) e cos(w) nas equações (I) e (II) obtemos os valores 
de x e y.





Robÿffffe9rio Alves escreveu:

> Se eu tenho o ponto (4,3) e girá-lo 60° anti-horário com mesmo módulo, 
> qual será esse novo ponto?
>
> ------------------------------------------------------------------------
> Yahoo! Acesso Grátis 
> <%20http://us.rd.yahoo.com/mail/br/taglines/*http://br.acesso.yahoo.com//>: 
> Internet rápida e grátis. Instale o discador agora!
>
> ------------------------------------------------------------------------
> Esta mensagem foi verificada pelo E-mail Protegido Terra 
> <http://mail.terra.com.br/>.
> Scan engine: McAfee VirusScan / Atualizado em 22/04/2005 / Versão: 
> 4.4.00 - Dat 4475
> Proteja o seu e-mail Terra: http://mail.terra.com.br/
>