[Fwd: como inserir um pentágono em um círculo]

[Benjamin Hinrichs <hinsoft@xxxxxxxxx>]

Devido à problemas relacionados com o limite do tamanho das msgs
recebidas pelo majordomo este e-mail demorou alguns dias a mais para ser
enviado e tal.

Um abraço e feliz bug!!

Benjamin Hinrichs

-------- Original Message --------
Subject: como inserir um pentágono em um círculo
Date: Thu, 23 Dec 1999 11:37:20 -0200
From: Benjamin Hinrichs <hinsoft@sinos.net>
Organization: Hinsoft Corp.
To: obm-l <obm-l@mat.puc-rio.br>

Diferente de todos os métodos anteriormente mostrados por vcs para achar
o sen36°, eu me utilizei do teorema (que aliás queria saber se só
achando os valores de seno e cosseno e mais o diabo é uma prova que o
teorema é válido) explicado e demonstrado com figurinhas abaixo:

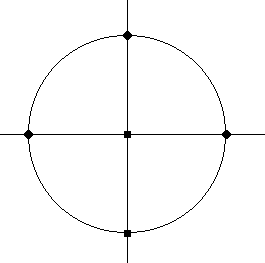
fig 1: desenha-se um círculo de centro em (0,0), para facilitar meu
trabalho, de raio r e retas que o dividam em quatro quadrantes iguais
(x=0 e y=0)
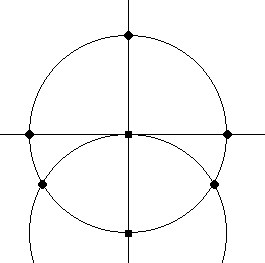
fig 2: traça-se um círculo com centro em algum lugar na circunferência
(no exemplo, no ponto (0,-r)) e raio r, tal que passe pelo centro do
primeiro círculo (ora, todas fariam isto). Os pontos onde os círculos se
cortam estão em destaque.
fig 3: traça-se a reta y=r/2 (neste exemplo), ou seja, uma reta que
passe pelos pontos de interesecção dos dois círculos. O ponto onde se
cortam esta reta e aquela divisória do quadrante será o centro do
próximo círculo.
fig 4: traça-se uma circunferência com raio r(sqrt(5))/2, ou seja, que
corte os pontos (-r,0) e (r,0). O ponto onde esta circunferência corta
y=0 e que se localiza dentro do círculo é destacado (com uma linda cor,
lilás...).
OBS: o lado de um heptano regular em relação ao raio r que corta seus
vértices é esta, se não me engano: r(sqrt(5))/2
fig 5: a distância entre o ponto lilás e o ponto (r,0) (ou (-r,0), já
que distância é igual ao módulo da distância, bla bla bla.) é o lado do
pentágono.

Com base nestas informações:
para menos sabidos (como eu): ache os valores de sen 36° e cos 54° (que
por sinal assumem valores iguais)
para os mestres: prove este teorema (e aproveite e dê uma olhada em suas
mentes para achar a origem deste teorema, acho que foi Euclides, mas
isto é um chute pra fora, aposto)


Um grande abraço e boas festas a todos bons cristãos; aos demais (como
eu) apenas um feliz ano novo.

Benjamin Hinrichs