P4 de Álgebra Linear I - 2001.2

Data: 3 de dezembro de 2001.

to to 0.7Nome:  Matrícula: to to 0.7Assinatura: Turma:

Questão	Valor	Nota	Revis.
1	2.5
2a	0.5
2b	0.5
2c	0.5
2d	0.5
3a	0.5
3b	0.5
3c	1.0
3d	0.5
3e	0.5
4a	1.5
4b	0.5
4c	1.0
Total	10.5

Instruções:

• Não é permitido usar calculadora. Mantenha o celular desligado.

• É proibido desgrampear a prova. Prova com folhas faltando ou rasuradas terá nota zero.

• Nas questões 2, 3 e 4 justifique cuidadosamente todas as respostas de forma completa, ordenada e coerente. Escreva de forma clara e legível.
• Nas questões 2, 3 e 4 da prova não haverá pontuação menor que 0.5 - Verifique cuidadosamente suas respostas.
• Faça a prova na sua turma.

Marque no quadro as respostas da primeira questão. Não é necessário justificar esta questão.

ATENÇÃ0: resposta errada vale ponto negativo!, a questão pode ter nota negativa!

Para uso exclusivo do professor	*****	*****
Certas:	$\times$ 0.3
Erradas:	$\times$ -0.2
*****	Total

1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque com caneta sua resposta no quadro abaixo. Atenção: responda todos os itens, use "N = não sei" caso você não saiba a resposta. Cada resposta certa vale 0.3, cada resposta errada vale -0.2, cada resposta N vale 0. Respostas confusas e ou rasuradas valerão -0.2.

Itens	V	F	N
1.a
1.b
1.c
1.d
1.e
1.f
1.g
1.h
1.i

1.a) Se $A=\left[ \begin{array}{ll} a & b \\ c & d \end{array}\right]$ e existem vetores u e w tais que Au=2u e Aw=-w, então a soma dos autovalores de A⁶ é igual a 63.

1.b) A distância entre o plano de equação x+y+z=0 e o plano de equação x+y+z=1 é igual a 1.

1.c) A reta de equações x=y=z é paralela ao plano de equação 2x-y-z=3.

1.d) O volume do paralelepípedo formado pelos vetores $(\frac{1}{\sqrt{2}}, \, 0, \, -\frac{1}{\sqrt{2}})$, $(\frac{1}{\sqrt{2}}, \, 0, \, \frac{1}{\sqrt{2}})$ e $(0,\, 1,\, 0)$é igual a 3.

1.e) É possível encontrar dois vetores u e v não nulos no plano tais que $\parallel u + v \parallel = \parallel u - v \parallel$.

1.f) Se u, v e w são três vetores de ${\mathbb R}^3$perpendiculares entre si, então existem $\alpha$, $\beta$ e $\gamma$números reais não nulos tais que $\alpha u +\beta v +\gamma w = \vec 0$.

1.g) Seja T uma matriz ortogonal. Então se $Tv=\vec 0$, então $v=\vec 0$.

1.h) Se -1, 1 e 1 (isto é, 1 tem multiplicidade 2) são os autovalores de uma matriz A $3\times 3$, então A representa um espelhamento com relação a um plano.

1.i) Se R é uma rotação de 90^o em ${\mathbb R}^3$ e se unão pertence ao eixo de rotação, então $u \cdot Ru =0$, isto é, u e R(u) são ortogonais.

2) Considere as retas r e s definidas pelas equações:

$$r:\left\{ \begin{array}{cccccccccc} x & + & y & + & z & = & 0 &\\ x & - & y & & & = & 1 &\\ \end{array}\right.$$

$$s:\left\{ \begin{array}{cccccccccc} x & = & 0 & + & t &\\ ... ... & -1 & + & 2t &\\ \end{array}\right. \quad t\in \mathbb{R} .$$

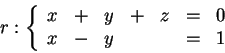
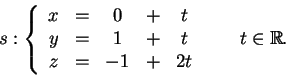
2.a) Determine uma equação paramétrica de r.

2.b) Determine uma equação cartesiana de s, isto é, escreva s como interseção de dois planos dados em equações cartesianas.

2.c) Estude a posição relativa de r e s.

2.d) Se a sua resposta no item (2.c) foi reversas ou paralelas calcule a distância entre r e s, e se foi se intersectam determine a equação cartesiana do plano que contém as retas r e s.

3) Considere $\beta=\{(1,1,0), (1,0,1), (0,1,1), (0,1,0)\}$.

3.a) Estude se $\beta$ é uma base de ${\mathbb R}^3$.

3.b) Considere uma transformação linear A de ${\mathbb R}^3$em ${\mathbb R}^3$ verificando

$$A(1,1,0)=(1,0,1), \quad A(1,0,1)=(0,1,1), \quad A(0,1,1)=(1,0,1).$$

Estude se A é ortogonal.

3.c) Determine a matriz de A na base canônica.

3.d) Determine um autovalor e um autovetor (associado ao autovalor encontrado) de A.

3.e) Encontre uma base onde a matriz de A é da forma

$$\left( \begin{array}{llll} 0 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right) \ .$$

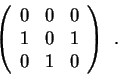
4) Considere a matriz

$$P=\left( \begin{array}{ccc} 2/3 & a & b \\ -1/3 & 2/3 & c \\ -1/3 & -1/3 & d \end{array}\right) \ .$$

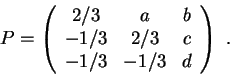
4.a) Determine a, b, c e d para que P represente uma projeção ortogonal em um plano. Determine a equação do plano de projeção.

4.b) Considere agora a matriz

$$A= \left( \begin{array}{ccc} 1/\sqrt{2} & 1/\sqrt{6} &1/\sqrt... ...6}\\ 1/\sqrt{3} & -1/\sqrt{3}& 1/\sqrt{3} \end{array}\right).$$

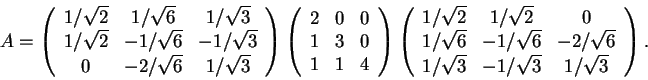
Determine os autovalores de A.

4.c) Finalmente considere a matriz

$$B= \left( \begin{array}{ccc} 1/\sqrt{2} & 1/\sqrt{6} &1/\sqrt... ...6}\\ 1/\sqrt{3} & -1/\sqrt{3}& 1/\sqrt{3} \end{array}\right).$$

Interprete geometricamente B. Nos casos envolvendo projeções determine a reta ou plano de projeção, nos casos envolvendo espelhamentos determine o plano ou reta de espelhamento, e nos casos envolvendo rotações determine o ângulo e o eixo de rotação.