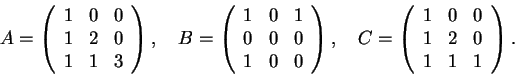P3 de Álgebra Linear I - 2002.1

Data: 7 de junho de 2002.

1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque com caneta sua resposta no quadro abaixo. Atenção: responda todos os itens, use "N = não sei" caso você não saiba a resposta. Cada resposta certa vale 0.3, cada resposta errada vale -0.2, cada resposta N vale 0. Respostas confusas e ou rasuradas valerão -0.2.

1.a) Seja A uma matriz simétrica inversível. Então sua inversa também é simétrica.

1.b) A multiplicação de duas matrizes simétricas é uma matriz simétrica.

1.c) Sejam A uma matriz $3\times 3$ e D uma matriz diagonal tais que A=P D P^-1 (onde P é uma matriz $3\times 3$inversível). Então A é simétrica.

1.d) Seja A uma matriz $3\times 3$ diagonalizável. Suponha que B=P A P^-1 (onde P é uma matriz $3\times 3$inversível). Então B é diagonalizável.

1.e) Sejam A uma matriz $3\times 3$ e $\sigma$ e $\lambda$ autovalores de A. Então $\sigma+\lambda$ é um autovalor de A.

1.f) Seja R uma rotação de $\mathbb{R} ^3$ de ângulo $\alpha$ e eixo de rotação a reta r que contém a origem. Então, para todo vetor não nulo u de $\mathbb{R} ^3$, se verifica que o ângulo entre u e R(u) é $\alpha$.

1.g) Seja A uma matriz ortogonal $3\times 3$. Então o determinante de A é $\pm 1$.

1.h) Seja A uma matriz diagonalizável. Então A³ também é diagonalizável.

1.i) Seja A uma matriz $2\times 2$ ortogonal e simétrica. Então A é a identidade ou representa um espelhamento.

2) Considere a matriz

$$A= \left( \begin{array}{cc} 1/2 & a\\ b & c \end{array}\right).$$

Determine

(2.a) a, b e c para que A represente uma projeção ortogonal,

(2.b) a, b e c para que A represente um espelhamento,

(2.c) a, b e c para que A represente uma rotação.

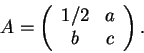
Considere agora a matriz B

$$B= \left( \begin{array}{ccc} 1/3 & a &b\\ 1/3 & c &d\\ 1/3 & e & f \end{array}\right).$$

(2.d) Determine a, b, c, d, e e fpara que B represente uma projeção ortogonal em uma reta.

(2.e) Determine a reta de projeção de B.

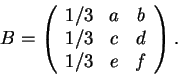
3) Considere a transformação linear $T\colon \mathbb{R} ^3\to \mathbb{R} ^3$tal que

$$T(1,1,1)=(-1,-1,-1), \quad T(1,1,-2)=(1,1,-2).$$

Sabendo que a matriz de T é simétrica e possui determinante zero:

(3.a) Determine os autovalores de T.

(3.b) Determine uma base de autovetores de T.

(3.c) Escreva T da forma T=PD P^-1 onde D é uma matriz diagonal.

(3.d) Calcule explicitamente T¹⁰⁰⁰.

4) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma diagonal das matrizes.

$$A= \left( \begin{array}{ccc} 1 & 0 &0\\ 1 & 2 &0\\ 1 & 1 & ... ...ay}{ccc} 1 & 0 &0\\ 1 & 2 &0\\ 1 & 1 & 1 \end{array}\right).$$