


Next: About this document ...
P3 de Álgebra Linear I - 2001.2
Data: Sábado, 24 de novembro de 2001.
to to .7Nome:
Matrícula:
to to
0.7Assinatura: Turma:
| Questão |
Valor |
Nota |
Revis. |
|
|
|
|
|
| 1a |
0.5 |
|
|
|
|
|
|
|
| 1b |
1.0 |
|
|
|
|
|
|
|
| 1c |
0.5 |
|
|
|
|
|
|
|
| 1d |
0.5 |
|
|
|
|
|
|
|
| 2a |
0.5 |
|
|
|
|
|
|
|
| 2b |
0.5 |
|
|
|
|
|
|
|
| 2c |
0.5 |
|
|
|
|
|
|
|
| 2d |
0.5 |
|
|
|
|
|
|
|
| 3a |
1.0 |
|
|
|
|
|
|
|
| 3b |
1.0 |
|
|
|
|
|
|
|
| 3c |
1.0 |
|
|
|
|
|
|
|
| 4a |
1.0 |
|
|
|
|
|
|
|
| 4b |
1.0 |
|
|
|
|
|
|
|
| 4c |
0.5 |
|
|
|
|
|
|
|
| Total |
10.0 |
|
|
|
|
|
|
|
Instruções:
-
Não é permitido usar calculadora.
Mantenha o celular desligado.
-
É proibido desgrampear a prova. Prova
com folhas faltando ou rasuradas terá nota zero.
-
Justifique todas as respostas de forma completa,
ordenada e coerente. Escreva de forma
clara e legível.
-
Em cada uma das questões da prova não haverá
pontuação menor que 0.5 - Verifique cuidadosamente suas
respostas.
-
Faça a prova na sua turma.
1)
Seja
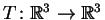 uma
transformação linear ortogonal.
Suponha que o determinante da matriz de T na base canônica é
-1 e que
uma
transformação linear ortogonal.
Suponha que o determinante da matriz de T na base canônica é
-1 e que
- a)
Determine um autovalor de T.
- b)
Determine T(1,-2,1).
- c)
Determine T(1,0,0).
- d)
Determine a matriz de T em uma base ortonormal
(v. escolhe a base e deve especifica-la).
2)
Seja A uma matriz 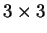 .
Suponha que
.
Suponha que
- a)
Estude se A é inversível.
- b)
Estude se A pode ser encontrada de maneira que A seja semelhante à
matriz diagonal
isto é,
A=P D P-1,
- c)
Estude se A pode ser encontrada de maneira que A seja semelhante à
matriz
- d)
Suponha agora que A é simétrica.
Estude se A pode ser encontrada de maneira que seja semelhante à
matriz
3)
Estude que tipo de transformações representam as matrizes.
No casos envolvendo
projeções determine a reta ou plano de projeção,
nos casos envolvendo espelhamentos determine
o plano ou reta de espelhamento,
e nos casos envolvendo rotações determine o
ângulo e o eixo de rotação.
4)

- a)
Seja A uma matriz simétrica
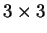 .
Sabendo que
A2001=-I(I é a matriz identidade), determine A.
.
Sabendo que
A2001=-I(I é a matriz identidade), determine A.
- b)
Estude se existe uma matriz simétrica
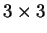 ,
B,
tal que
B2000=-I.
,
B,
tal que
B2000=-I.
- c)
Estude se é verdadeira a afirmação seguinte:
Seja C uma matriz
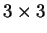 tal que C5=0. Então Cé a matriz zero.
tal que C5=0. Então Cé a matriz zero.



Next: About this document ...
Lorenzo J. Diaz
2001-11-26
![]() uma
transformação linear ortogonal.
Suponha que o determinante da matriz de T na base canônica é
-1 e que
uma
transformação linear ortogonal.
Suponha que o determinante da matriz de T na base canônica é
-1 e que
![]() .
Suponha que
.
Suponha que
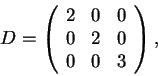
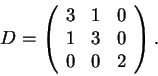
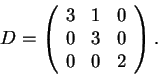
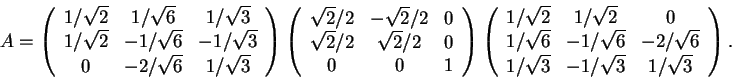
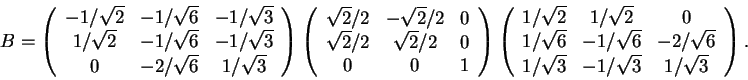
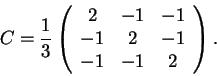
![]()