


Next: About this document ...
P2 de Álgebra Linear I - 2001.2
Data: Sábado, 20 de outubro de 2001.
to to .7Nome:
Matrícula:
to to
0.7Assinatura: Turma:
| Questão |
Valor |
Nota |
Revis. |
|
|
|
|
|
| 1 |
3.5 |
|
|
|
|
|
|
|
| 2a |
1.0 |
|
|
|
|
|
|
|
| 2b |
1.0 |
|
|
|
|
|
|
|
| 2c |
0.5 |
|
|
|
|
|
|
|
| 2d |
0.5 |
|
|
|
|
|
|
|
| 3a |
0.5 |
|
|
|
|
|
|
|
| 3b |
1.0 |
|
|
|
|
|
|
|
| 3c |
1.0 |
|
|
|
|
|
|
|
| 3d |
0.5 |
|
|
|
|
|
|
|
| 3e |
0.5 |
|
|
|
|
|
|
|
| Total |
10.0 |
|
|
|
|
|
|
|
Instruções:
-
Não é permitido usar calculadora.
Mantenha o celular desligado.
-
É proibido desgrampear a prova. Prova
com folhas faltando terá nota zero.
-
Justifique todas as respostas. Escreva de forma
clara, legível e organizada.
-
Em cada uma das questões da prova não haverá
pontuação menor que 0.5 - Verifique cuidadosamente suas
respostas.
-
Faça a prova na sua turma.
1)
Estude se as afirmações a seguir são verdadeiras ou falsas.
Justifique cuidadosamente sua resposta. Nos casos afirmativos
encontre a matriz da transformação linear envolvida.
- a)
Existe uma rotação R tal que
R(2,1)=(1,3).
- b)
Existe um espelhamento ou reflexão E tal que
E(1,1)=(-1,1) e
E(-1,1)=(1,-1).
- c)
Existe uma projeção ortogonal P tal que
P(1,1)=(1/2,-1/2) e
P(2,1)=(1/3,2/3).
- d)
Existe um espelhamento ou reflexão E tal que
E(1,1)=(1,1) e
E(2,1)=(-2,-1).
- e)
Existe um espelhamento ou reflexão E tal que
E(2,1)=(-1,-2).
- f)
Existe uma transformação linear
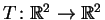 tal que
T(1,1)=(5,7),
T(2,1)=(1,0) e
T(3,2)=(1,2).
tal que
T(1,1)=(5,7),
T(2,1)=(1,0) e
T(3,2)=(1,2).
2)
Considere a transformação linear L,
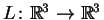 definida por
definida por
- a)
Determine L(1,0,0) e L(0,0,1).
- b)
Determine a matriz de L.
- c)
Calcule L(1,2,3).
- d)
Estude se L é inversível.
3)
Considere os vetores
- a)
Estude se os vetores
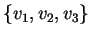 formam uma base
de
formam uma base
de
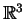 .
.
Dado um vetor w escreva
w=a v1 +b v2 +c v3
e considere a transformação linear
- b)
Determine T(0,1,0) e T(0,0,1)
- c)
Determine a matriz de T.
- d)
Estude se T é inversível. Caso afirmativo encontre
a matriz T-1.
- e)
Determine a matriz de
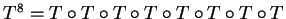 .
.



Next: About this document ...
Lorenzo J. Diaz
2001-10-20
![]() definida por
definida por