


Next: About this document ...
P1 de Álgebra Linear I - 2001.2
Data: Sábado, 15 de setembro de 2001.
to to .7Nome:
Matrícula:
to to
0.7Assinatura: Turma:
| Questão |
Valor |
Nota |
Revis. |
 |
Questão |
Valor |
Nota |
Revis. |
| 1a |
0.5 |
|
|
|
3a |
0.5 |
|
|
| 1b |
0.5 |
|
|
|
3b |
0.5 |
|
|
| 1c |
0.5 |
|
|
|
3c |
0.5 |
|
|
| 1d |
0.5 |
|
|
|
3d |
0.5 |
|
|
| 1e |
0.5 |
|
|
|
3e |
0.5 |
|
|
| 2a |
0.5 |
|
|
|
4a |
0.5 |
|
|
| 2b |
0.5 |
|
|
|
4b |
0.5 |
|
|
| 2c |
0.5 |
|
|
|
4c |
0.5 |
|
|
| 2d |
0.5 |
|
|
|
4d |
1.0 |
|
|
| 2e |
0.5 |
|
|
|
|
|
|
|
| Total |
10.0 |
|
|
|
|
|
|
|
Instruções:
-
Não é permitido usar calculadora.
Mantenha o celular desligado.
-
Justifique todas as respostas. Escreva de forma
clara, legível e organizada.
-
Em cada uma das questões da prova não haverá
pontuação parcial - Verifique cuidadosamente suas
respostas.
-
Faça a prova na sua turma.
1)
Sejam u e v vetores unitários de
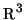 .
.
- a)
Suponha que
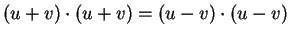 .
Calcule o ângulo formado pelos vetores
u e v.
.
Calcule o ângulo formado pelos vetores
u e v.
- b)
Suponha que
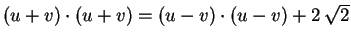 .
Calcule o ângulo formado pelos vetores
u e v.
.
Calcule o ângulo formado pelos vetores
u e v.
- c)
Suponha que
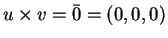 .
Calcule
.
Calcule
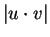 .
.
- d)
Considere um vetor n. Sabendo que
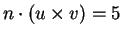 ,
calcule
,
calcule
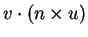
- e)
Considere um vetor não nulo n. Calcule
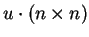 .
.
2)
Considere o plano
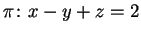 .
.
- a)
Determine a equação cartesiana do plano
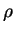 paralelo
a
paralelo
a 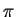 que contém a origem.
que contém a origem.
- b)
Determine as equações paramétricas de
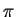 .
.
- c)
Calcule a distância entre os planos
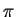 e
e 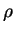 (onde
(onde 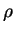 é o plano obtido em (a)).
é o plano obtido em (a)).
- d)
Calcule o ponto de
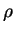 mais próximo do ponto
(1,0,1) de
mais próximo do ponto
(1,0,1) de 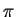 .
.
- e)
Determine um triângulo retângulo com dois vértices
em
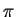 e um vértice em
e um vértice em 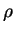 .
.
3)
Considere a reta r1 dada como intersecção dos planos
x-z=1 e x-y=1. Seja a reta
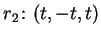 ,
,
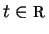 .
.
- a)
Determine um vetor diretor de r1.
- b)
Determine uma equação paramétrica de r1.
- c)
Escreva a reta r2 como intersecção de dois planos
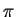 e
e 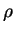 dados em equações paramétricas.
dados em equações paramétricas.
- d)
Calcule a distância entre as retas r1 e r2.
- e)
Determine a posição relativa das retas r1 e r2.
4)
Considere os planos
e a reta
- a)
Determine a posição relativa de
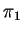 e
e 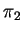 .
.
- b)
Determine a posição relativa de
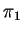 e
e 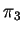 .
.
- c)
Determine a posição relativa de
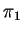 ,
,
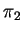 e
e 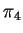 .
.
- d)
Determine a posição relativa de
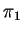 e r.
e r.



Next: About this document ...
Lorenzo J. Diaz
2001-09-15
![]() .
.
![]() .
.
![]() ,
,
![]() .
.