P4 de Álgebra Linear I - 2002.2

Data: 2 de dezembro de 2002

Gabarito

1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque com caneta sua resposta no quadro abaixo. Atenção: responda todos os itens, use "N = não sei" caso você não saiba a resposta. Cada resposta certa vale 0.3, cada resposta errada vale -0.2, cada resposta N vale 0. Respostas confusas e/ou rasuradas valerão -0.2.

Itens	V	F	N
1.a		F
1.b		F
1.c		F
1.d	V
1.e	V
1.f		F
1.g	V

1.a) Os vetores (1,1,1), (1,2,1) e (1,3,1) formam uma base de $\mathbb{R} ^3$.

Falso: É suficiente ver que não são linearmente independentes. Para isto é suficiente verificar que

1.b) Sejam E um espelhamento de $\mathbb{R} ^2$ e R uma rotação de $\mathbb{R} ^2$. A composição $E\circ R$ é uma rotação.

Falso: O determinante

Mas o determinante de uma rotação é 1.

1.c) Toda matriz $3\times 3$ triangular é diagonalizável. Falso: Considere a matriz triangular

O único autovalor da matriz é 1, e os autovetores associados são da forma (0,t), $t\ne 0$. Logo é impossível encontrar uma base de autovetores, portanto, a matriz não é diagonalizável.

1.d) As matrizes

são semelhantes. Verdadeiro: As duas matrizes são triangulares com a diagonal formada por números diferentes. Logo as duas matrizes têm autovalores (correspondentes à diagonal) 77777, 88888 e 99999. Como possuem três autovalores diferentes, as matrizes são diagonalizáveis, e uma forma diagonal delas é

Logo A e B são semelhantes a D, isto é,

Portanto,

D=P^-1A P.

Logo, substituindo D,

B=QP^-1 A P Q^-1= (QP^-1) A (QP^-1)= MAM^-1,

onde

M=QP^-1.

Isto é, as matrizes A e B são semelhantes.

1.e) A matriz

possui uma base ortonormal de autovetores.
Verdadeiro: Se trata de uma matriz simétrica.

1.f) As retas $r\colon (t,1+t,1+t)$ e $s\colon (2t,1+2t, -t)$, $t\in \mathbb{R}$, são reversas.
Falso: Veja primeiro que não são paralelas (os vetores diretores não são paralelos). Para ver se são reversas é suficiente ver se as retas se interceptam. Ou seja, ver se o sistema tem solução:

Da primeira e da segunda equações temos, $t=2\,s$. Logo, substituindo na terceira,

Logo as retas se encontram no ponto (-2/3, 1/3,1/3), logo não são reversas.

1.g) Seja A uma matriz $3\times 3$ ortogonal e simétrica cujo traço é igual a 3. Então A é a identidade.
Verdadeiro: Como A é simétrica, seus autovalores são reais. Como A é ortogonal, seus autovalores são $\pm 1$. Logo as possibilidades para os autovalores de A são:

• 1 com multiplicidade 3, e o traço é 3,
• 1 com multiplicidade 2 e -1 simples, e o traço é 1,
• 1 um autovalore simples e -1 com multiplicidade 1, e o traço é -1,
• -1 com multiplicidade 3, e o traço é -3.

Logo a única possibilidade é a primeira. Em tal caso a forma diagonal de A é a identidade. Logo A é semelhante a identidade. Logo é a própria identidade:

A=P (Id) P^-1= P P^-1 =(Id).

2) Escolha qual das afirmações a seguir é a verdadeira e marque com caneta sua resposta no quadro abaixo. Atenção: responda todos os itens, use "N = não sei" caso você não saiba a resposta. Cada resposta certa vale 0.6, cada resposta errada vale -0.1, cada resposta N vale 0. Respostas confusas e/ou rasuradas valerão -0.1.

Itens	a	b	c	d	e	f	N
2.1					e
2.2				d
2.3			c
2.4		b

Considere a matriz

(2.1) O polinômio característico de A é:

(a) $-\lambda^3+ 5\, \lambda^2-6\lambda +1$.

(b) $-\lambda^3+ 2\, \lambda^2-4\lambda +5$.

(c) $-\lambda^3+ 2\, \lambda^2-4\lambda +1$.

(d) $-\lambda^3+ 6\, \lambda^2-2\lambda -5$.

(e) $-\lambda^3+ 4\, \lambda^2-5\lambda +2$.

(f) Nenhuma das opções anteriores, todas estão erradas.

(2.2) Os autovalores de A são:

(a) 1 (simples) e 2 (de multiplicidade 2).

(b) 0 e 2 (de multiplicidade 2),

(c) 1, -1 e 3,

(d) 1 (de multiplicidade 2) e 2 (simples),

(e) 0, 4 e -1,,

(f) Nenhuma das opções anteriores, todas estão erradas.

(2.3) Estude as seguintes afirmações sobre os autovetores de A:

(a) Os vetores (1,0,1), (0,1,-1) e (1,1,2) correspondentes as colunas da matriz A são autovetores de A.

(b) Os vetores (1,0,1), (0,1,1) e (1,-1,2) correspondentes as linhas da matriz A são autovetores de A.

(c) Os vetores (1,1,1) e (1,1,0) são autovetores de A.

(d) Os vetores (1,1,1), (0,1,1) e (1,1,0) são autovetores de A.

(e) A matriz A não é simétrica, portanto não possui nenhum autovetor.

(f) Nenhuma das opções anteriores, todas estão erradas.

(2.4) Considere a base $\beta=\{(1,1,1), (0,1,1), (1,1,0)\}$. A matriz de A na base $\beta$ é:

(a)

(b)

(c)

(d)

(e)

(f) Nenhuma das opções anteriores, todas estão erradas.

Resposta:

(2.1) O polinômio característico de A é o determinante

Logo a resposta correta é (e).

Comentários: Observe que o traço da matriz A é 4. Como o traço é o coeficiente do termo de grau (n-1) (n o tamanho da matriz) do polinômio característcio, no nosso caso, n=3. Logo as possibilidades (a),(b),(c) e (d) estão descartadas. Observe também que o determinante de A é

Como o determinante é o coeficiente independente do polinômio caracteístico, isto também descarta as possibilidades (a),(b),(c) e (d).

(2.2) Os cálculos do item anterior implicam que os autovalores são 1, de multiplicidade dois, e 2 simples. Logo a resposta correta é (d).

Comentários: Como o traço de A é 4, e o traço é a soma dos autovalores contados com multiplicidade, as possibilidades (a), (c) e (e) estão descartadas. Como o determinante de A é 2 e coincide com o produto dos autovalores (considerados com multiplicidade), as possibilidades (a),(b),(c) e (e) estão descartadas.

(2.3) Para responder a este item devemos determinar os autovetores de A associados a 1 e 2. Os autovetores de 1 são os vetores não nulos (x,y,z) que verificam

ou seja,

Ou seja os vetores da forma (t,t,0), $t\ne 0$. Observe que 1 tem multiplicidade 2 e somente é possível obter um autovetor associado (isto é, todos seus autovetores são paralelos). Portanto, A não é diagonalizável. Os autovetores associados a 2 são os vetores não nulos (x,y,z) que verificam

ou seja,

Ou seja os vetores da forma (t,t,t), $t\ne 0$. Dos comentários anteriores temos que: A não possui uma base de autovetores, e os autovetores de A são os vetores não nulos da forma (t,t,t) e (t,t,0). Logo (1,1,1) e (1,1,0) são autovetores de A, e o item (c) é verdadeiro. Vejamos agora as possíveis respostas. Fazendo os cálculos (e dos comentários acima) temos que (a) é falso: A(1,0,1)=(2,1,3)! Isto também implica que (b) é falso. Analogamente, (0,1,1) não é autovetor, logo (d) é falso. Finalmente, a última afirmação é um disparate completo.

(2.4) Fazemos u=(1,1,1), v=(0,1,1) e w=(1,1,0). Já sabemos que A(1,1,1)=2(1,1,1) e que A(1,1,0)=(1,1,0). Logo

Finalmente,

A(0,1,1)=(1,2,1).

Devemos escrever este vetor na base $\beta$:

(1,2,1)=x(1,1,1)+y(0,1,1)+z(1,1,0),

ou seja,

Portanto, da primeira e terceira equações, y=z e

Logo y=1=z. Portanto, x=0. Logo

A(v)=v+w.

Isto implica que a matriz de A na base $\beta$ é a matriz do item (b).

Comentários: Como a matriz A é semelhante a matriz de A na base $\beta$, devem necessariamente ter o mesmo traço e o mesmo determinante. Como neste caso todas as matrizes têm determinante igual a 2 e traço 4, não é possí vel descartar a priori (usando este critério) nenhuma possibilidade. De uma outra forma, lembre que $A(u)=2\,u$. Se a primeira matriz estivesse correta teríamos a contradição A(u)=u!. Similarmente, na matriz de (c), $A(u)=u+v\ne 2\,u$!. No caso da matriz (d) teríamos que A seria diagonalizável, e pelos comentários já feitos sabemos que isto é falso. Finalmente, na matriz de (e) fornece $A(v)=u+v+w\ne v+w$! 3) Dados o plano $\pi\colon x+y-z=0$ e a reta r=(-t,t,t), $t\in \mathbb{R}$ considere a transformação linear M definida como segue. Dado um ponto P=(x,y,z), considere o vetor $\overline{OP}= (x,y,z)$ e defina

$$M(\overline{OP})=\overline{OQ},$$

onde Q é o ponto de interseção do plano $\rho$ contendo o ponto P e paralelo a $\pi$ e a reta r. Veja a figura. Considere também a transformação linear L definida como segue,

$$L(\overline{OP})=\overline{OT},$$

onde T é o ponto do plano $\rho$ tal que Q é equidistante de T e de P e os pontos P, T e Q são colineares. Veja a figura.

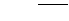
pi$\pi$ ro$\rho$ rr ww v=OP $v=\overline{OP}$ PP QQ OO vv TT M(v)M(v) L(v)L(v) Av=M(v)+w B L(v)=M(v)-w

a) Determine a matriz da transformação linear M.

b) Determine a matriz da transformação linear L.

c) Determine uma base de autovetores de M.

d) Determine uma base de autovetores de L.

e) Determine uma forma diagonal de M.

f) Estude se é possível escrever M da forma

M=PDP^t,

onde P é ortogonal.

Resposta: (a) Resolveremos o problema de três formas diferentes. Primeiro usando geometria analítica. Considere o vetor v=(a,b,c) e o ponto P=(a,b,c). O plano contendo P paralelo a $\pi$ é

A interseção de $\rho$ e r ocorre quando o parâmetro t verifica

Ou seja, no ponto

(a+b-c,-a-b+c,-a-b+c).

Isto é

M(a,b,c)=(a+b-c,-a-b+c,-a-b+c).

Portanto,

Logo

Uma segunda forma é a seguinte. Observe que os vetores do plano $\pi$ se transformam no vetor nulo, e o vetor (1,-1,-1) nele próprio. Portanto, conhecemos as imagens dos vetores (1,0,1), (0,1,1) (vetores do plano) e (1,-1,-1) (vetor diretor da reta) que formam uma base. Logo, M está determinada. Escrevendo

(1,0,0)=(1,-1,-1)+(0,1,1),

temos

M(1,0,0)= M(1,-1,-1)+M(0,1,1)= (1,-1,-1).

Analogamente, escrevendo

(0,1,0)=x(1,-1,-1)+y (0,1,1)+z(1,0,1)

temos

logo z=-1, x=1 e y=2. Portanto,

Finalmente,

(0,0,1)=x(1,-1,-1)+y (0,1,1)+z(1,0,1)

temos

logo z=-x, x=y, e z=1 e x=y=-1. Assim,

E obtemos a matriz acima.

Existe um último método. Considere a base

A base $\beta$ é uma base de autovetores de M (estamos respondendo ao item (c)!), cujos autovetores são 1, 0 e 0. Logo a matriz de M na base $\beta$ é

que é precisamente uma forma diagonal de M (estamos respondendo ao item (e)!). Portanto,

onde P é a matriz de mudança da base $\beta$ à canônica:

Faça os cálculos (que são simples) usando, por exemplo, o Método de Gauss e veja que

Portanto,

Obtendo novamente a mesma matriz.

(b) Dado um vetor v escreva,

v=M(v)+w.

Logo

w=v-M(v)=Id(v)-M(v).

Por definição,

Ou seja,

Isto é,

Verifique o que v. já sabe geometricamente:

Assim estamos respondendo ao item (d), obtendo uma base de autovetores de L.

(c) A base já foi obtida:

(d) A base já foi obtida:

(e) Uma forma diagonal já foi obtida:

(f) Não é possível. Em primeiro lugar, se fosse possível M seria ortogonalmente diagonalizável, portanto, simétrica, o que já sabemos que não acontece (veja a matriz de M!). Caso v. não tenha obtido a matriz M pode raciocinar geometricamente: a matriz não é ortogonalmente diagonalizável, pois o autovetor (1,-1,-1) associado a 1 não é ortogonal ao plano x+y-z=0, onde estão os autovetores associados a 0. 4) Considere as retas $r\colon (t,1-t,2\,t)$ e s obtida como interseção dos planos $\pi\colon x+2y-z=1$ e $\rho\colon 2x+y+z=2$.

a) Determine uma equação paramétrica de s.

a) Determine a equação cartesiana do plano $\eta$ normal a r que contém o ponto (1,2,3).

c) Determine a posição relativa de r e s (reversas, paralelas, ou concorrentes).

d) Se as retas são reversas calcule a distância entre elas, se paralelas a equação do plano que as contém, e se concorrentes seu ponto de interseção.

Resposta: (a) Para calcular a equação é suficiente resolver o sistema

Escalonando,

Escolhendo y como parámetro (i.e. fazendo y=t) temos z=t e

x=1+z-2y=1 +t -2t=1-t.

Logo uma equação paramétrica da reta s é:

Observe que o ponto (1,0,0) pertence aos dois planos e que o vetor diretor da reta (-1,1,1) é ortogonal aos vetores normais dos planos $\pi$ e $\rho$. Logo o resultado é coerente.

(b) O vetor normal do plano $\rho$ é o vetor diretor de r, isto é, o vetor (1,-1,2). Portanto, a equação cartesiana de $\rho$ é da forma:

onde d é determinado pela condição $(1,2,3)\in \rho$:

Portanto, a equação cartesiana de $\rho$ é

(c) Como o vetor diretor de s é (1,-1,-1) e o de r é (1,-1,2) as retas não são paralelas. Para ver se são reversas ou concorrentes há duas possibilidades. A primeira é ver se o sistema

possui solução. Em caso afirmativo as retas são concorrentes e em caso negativo reversas. Observe que a primeira e a segunda equações são iguais. Substituindo o valor de $s=2\,t$ na primeira equação temos

Que fornece s=2/3. Logo o sistema possui solução é o ponto de interseção é

(1/3,2/3, 2/3).

Observe que (como deve ser) obtemos o mesmo ponto substituindo os parâmetros t e s obtemos o mesmo ponto. Vaja também que estamos respondendo ao item (d). Outra possibilidade para responder a questão é escolher um ponto de r (por exemplo, P=(0,1,0)), um ponto de s (por exemplo, Q=(1,0,0) e os vetores diretores v=(1,-1,2) de r e w=(1,-1,-1) de s e considerar o produto misto

$$\overline{QP}\cdot (v\times w)= (1,-1,0)\cdot ((1,-1,2)\times (1,-1,-1)).$$

Se o resultado é nulo as retas são concorrentes, e reversas em caso contrário. Temos

Logo as retas são concorrentes.

(d) O ponto de interseçõ já foi calculado: (1/3,2/3,2/3).