P4 de Álgebra Linear I - 2002.1

Data: 7 de junho de 2002.

Gabarito

1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque com caneta sua resposta no quadro abaixo. Atenção: responda todos os itens, use "N = não sei" caso você não saiba a resposta. Cada resposta certa vale 0.3, cada resposta errada vale -0.2, cada resposta N vale 0. Respostas confusas e ou rasuradas valerão -0.2.

1.a) Considere as retas de equações paramétricas

$$r=(p_1+tv_1, p_2+tv_2, p_3+tv_3), \quad \mbox{e} \quad s=(q_1+tw_1, q_2+tw_2, q_3+tw_3), \quad t\in \mathbb{R} .$$

Suponha que

$$(p_1-q_1,p_2-q_2,p_3-q_3)\cdot (v_1,v_2,v_3) \times (w_1,w_2,w_3)=0.$$

Então as retas se interceptam em um ponto.

Falso: As retas podem ser paralelas e diferentes (ou seja, com interseção vazia). Por exemplo, r=(1+t,0+t,0+t) e s=(t,t,t), $t\in \mathbb{R}$. Temos que p=(1,0,0), q=(0,0,0), v=w=(1,1,1). Claramente, $(1,0,0)\cdot (1,1,1)\times (1,1,1)= (1,0,0)\cdot (0,0,0)=0$. As retas são disjuntas, observe que o ponto (1,0,0) de r não pertence a s.

1.b) A multiplicação de duas matrizes ortogonais é uma matriz ortogonal.

Verdadeiro: Ser ortogonal significa, A A^t=I ou A^-1=A^t. Sejam A e B matrizes ortogonais. Portanto, A A^t=I e B B^t=I. Devemos ver que (AB)(AB)^t=I. Para isto é suficiente observar que

(AB)(AB)^t=ABB^tA^t = A(BB^t)A^t=AIA^t=AA^t=I.

1.c) Sejam A uma matriz $3\times 3$ cujo polinômio caraterístico é

$$p(\lambda)=-(\lambda-1)^2(\lambda-2).$$

Então A não é diagonalizável.

Falso: Considere a matriz

$$A=\left( \begin{array}{ccc} 1 & 0 &0\\ 0 & 1 & 0\\ 0 & 0 & 2 \end{array}\right).$$

O polinômio da matriz é $p(\lambda)=-(\lambda-1)^2(\lambda-2)$, e a matriz é diagonalizável (de fato já é diagonal!).

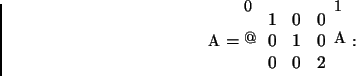
1.d) Seja A uma matriz $2\times 2$ ortogonal e simétrica. Então A representa um espelhamento.

Falso: Considere a matriz

$$A=\left( \begin{array}{ccc} -1 & 0 \\ 0 & -1 \end{array}\right).$$

Esta matriz não representa um espelhamento (seu traço é -2).

1.e) Considere o plano $\pi$ de equação cartesiana ax+by+cz=d e a reta r=(p₁+tv₁, p₂+tv₂, p₃+tv₃). Suponha que $(a,b,c)\cdot (v_1,v_2,v_3)=0$. Então a reta e o plano têm exatamente um ponto de interseção.

Falso: A condição significa que a reta é paralela ao plano. Portanto, ou é disjunta (nao há ponto de interseção) ou está contida (há infinitos pontos de interseção). Por exemplo, considere o plano x+y+z=1 e a reta (1+t,-1,1-t), $t\in \mathbb{R}$. Temos $(1,0,-1)\cdot (1,1,1)=0$ e a reta está contida no plano.

1.f) Considere a matriz

$$A= \left( \begin{array}{ccc} 0 &0 &1\\ 0& 6 &0 \\ 3 &0 &2 \end{array}\right).$$

Os autovalores de A são 0, 6 e 2.

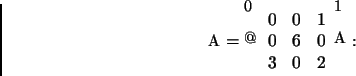
Falso: Se os autovalores fossem 0, 6 e 2 a matriz teria determinante nulo (o produto dos autovalores). Mas o determinante é $-18\ne 0$.

1.g) Considere uma transformação linear P de $\mathbb{R} ^3$ tal que $P^2=P\circ P=P$. Então P é uma projeção ortogonal.

Falso: Considere a identidade.

1.h) O produto de duas matrizes inversíveis é uma matriz inversível.

Verdadeiro: Observe que ser inversível é equivalente a ter determinante não nulo. Sejam A e B inversíveis. Então,

$$\det(AB)=\det(A)\det(B)\ne 0.$$

Logo AB é inversível.

1.i) Os vetores $\{(1,1,1), (1,0,-1), (1,-2,1)\}$formam uma base ortonormal.

Falso: Para formar uma base ortonormal os vetores devem ser ortogonais (como acontece neste caso) e unitários (o que não acontece neste caso), no nosso caso, os vetores possuem módulo $\sqrt{3}$, $\sqrt{2}$ e $\sqrt{6}$.

Itens	V	F	N
1.a		f
1.b	v
1.c		f
1.d		f
1.e		f
1.f		f
1.g		f
1.h	v
1.i		f

2) Considere o plano x+y+z=0, o ponto p=(1,1,1) e as retas r₁=(t,1-t,t) e r₂=(1-t, 1+t,t), $t\in \mathbb{R}$. Determine

(2.a) A equação da reta r que contêm o ponto p e é perpendicular a $\pi$.

(2.b) A equação do plano que contém o ponto p e é paralelo a r₁ e r₂.

(2.c) A distância entre as retas r₁ e r₂.

(2.d) A posição relativa das retas r₁ e r₂.

(2.e) A posição relativa da reta r₂ e o plano $\pi$.

Resposta: O vetor diretor da reta r é o vetor normal do plano, (1,1,1). Um ponto de r é (1,1,1). Logo uma equação paramétrica é (1+t, 1+t,1+t), $t\in \mathbb{R}$.

Caso v. prefira dar equações cartesianas, observe que os planos x-z=0 e y-z=0 contém a reta.

Seja $\rho$ o plano procurado. Os vetores diretores das retas (1,-1,1) e (-1,1,1) são vetores paralelos ao plano. Logo o vetor normal do plano pode ser obtido como $(1,-1,1)\times(-1,1,1)=(-2,-2,0)$. Logo o plano é da forma $\rho\colon x+y=d$, onde d é determinado por $(1,1,1)\in \rho$, ou seja d=1+1=2. Logo, $\rho\colon x+y=2$.

Para calcular a distância entre as retas consideramos o pontos $P=(0,1,0)\in r_1$ e $Q=(1,1,0)\in r_2$ e o vetor $\overline{PQ}=(1,0,0)$. A distância entre as retas é

$$\frac{\vert(1,0,0)\cdot (1,-1,1)\times (-1,1,1)\vert} {\vert\... ...2,-2,0)\vert\vert}= \frac{2} {2\sqrt{2}}= \frac{1} {\sqrt{2}}.$$

O item anterior mostra que as retas são reversas. Elas não são paralelas (pois os vetores diretores não são proporcionais). Logo ou são reversas ou se interceptam em um ponto (neste último caso a distância seria 0).

O vetor diretor de r₂ é (-1,1,1). O vetor normal ao plano é (1,1,1). Como $(-1,1,1)\cdot (1,1,1)=1\ne 0$ o plano e a reta não são paralelos. Logo se interceptam em um ponto.

3) Considere a projeção ortogonal P no plano 2x+2y+2z=0 e a projeção Q no plano x+y+z=0 na direção da reta (t,-t,0), $t\in \mathbb{R}$.

(3.a) Determine os autovalores de P e de Q.

(3.b) Determine bases de autovetores de P e de Q.

(3.c) Escreva P da forma P=MD M^-1, onde D é uma matriz diagonal. Determine explicitamente M e M^-1.

(3.d) Escreva Q da forma Q=NE N^-1, onde E é diagonal. Determine explicitamente N.

(3.e) Determine a relação entre as transformações $Q\circ P$ e P.

Resposta: Como se trata de uma projeção, os autovalores de P são 1 (com multiplicidade dois) e 0 (simples).

Respeito a projeção Q. A direção de projeção é paralela ao plano x+y+z=0, logo Q não está definida. Portanto, não é possível falar de autovetores nem autovalores de Q, nem da matriz associada a Q. Logo não é necessário responder a questão (3c). Respeito a (3d), a transformação $Q\circ P$ não está definida.

Uma base de autovetores de P está formada por dois vetores l.i. do plano de projeção (autovetores associados ao autovalor duplo 1) e um vetor normal (associado ao autovalor 0). Logo uma base é

$$\beta_1=\{(1,0,-1), (1,-2,1), (1,1,1)\}.$$

Uma forma diagonal de P é

$$D= \left( \begin{array}{ccc} 1 &0 &0\\ 0& 1 &0 \\ 0 &0 &0 \end{array}\right).$$

Uma base ortonormal $\beta$ de autovetores onde a matriz de P é D é

$$\beta= \{(1/\sqrt{2},0,-1/\sqrt{2}), (1/\sqrt{6},-2/\sqrt{6},1/\sqrt{6}), (1/\sqrt{3},1/\sqrt{3},1/\sqrt{3})\}.$$

Logo

$$M= \left( \begin{array}{ccc} 1/\sqrt{2} &1/\sqrt{6} &1/\sqrt{... ...3} \\ -1/\sqrt{2} &1/\sqrt{6} &1/\sqrt{3} \end{array}\right).$$

Como a matriz M é ortogonal (suas colunas são os vetores de uma base ortonormal), M^t=M^-1. logo

$$M^t= \left( \begin{array}{ccc} 1/\sqrt{2} &0 &-1/\sqrt{2}\\ ... ...{6} \\ 1/\sqrt{3} &1/\sqrt{3} &1/\sqrt{3} \end{array}\right).$$

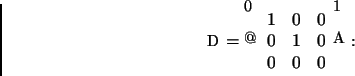
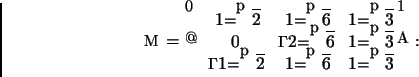
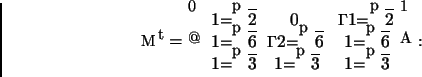
4) Considere a matriz

$$A= \left( \begin{array}{ccc} 1 &0 &3\\ 0& 6 &0 \\ 3 &0 &1 \end{array}\right).$$

(4.a) Determine os autovalores de A.

(4.b) Determine uma base de autovetores A.

(4.c) Determine uma forma diagonal D de A.

(4.d) Escreva A da forma A=MD M^-1 onde D é uma matriz diagonal. Determine explicitamente M e M^-1.

(4.e) Escreva, caso exista, a matriz A^-1 inversa de A da forma A^-1=NE N^-1, onde E é uma matriz diagonal. Determine explicitamente N e N^-1.

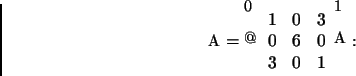
Resposta: O polinômio característico de A é

$$p(\lambda)= (6-\lambda)((1-\lambda)^2-9)) = (6-\lambda)(\lambda^2-2\lambda -8)$$

Observe que o polinômio $(\lambda^2-2\lambda -8)$ tem raízes $\lambda=4$ e $\lambda=-2$. Logo as raízes de $p(\lambda)$ são $\lambda=6,4,-2$. Observe que este resultado é coerente com o traço ser 8 e o determinante ser -48.

Uma base de autovetores é obtida da seguinte forma.

autovetores associados a 6: são as soluções não triviais do sistema,

$$\left( \begin{array}{ccc} 1-6 &0 &3\\ 0& 6-6 &0 \\ 3 &0 &1-... ...ht) = \left( \begin{array}{c} 0\\ 0 \\ 0 \end{array}\right).$$

Obtemos o sistema,

$$-5x +3y=0, \quad 3x-5y=0.$$

As soluções são da forma (0,t,0), $t\in \mathbb{R}$. Portanto, um autovetor é, (0,1,0).

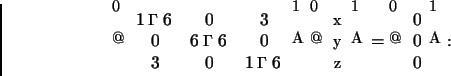
autovetores associados a 4: são as soluções não triviais do sistema,

$$\left( \begin{array}{ccc} 1-4 &0 &3\\ 0& 6-4 &0 \\ 3 &0 &1-... ...ht) = \left( \begin{array}{c} 0\\ 0 \\ 0 \end{array}\right).$$

Obtemos o sistema,

$$-3x +3y=0, \quad 3y=0, \quad 3x-3y=0.$$

As soluções são da forma (t,0,t), $t\in \mathbb{R}$. Portanto, um autovetor é, (1,0,1).

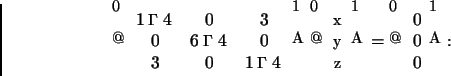
autovetores associados a -2: Como a matriz é simétrica, os autovetores associados a -2 devem ser ortogonais a (1,0,1) e (0,1,0). Logo um autovetor é (1,0,-1).

Portanto, uma base de autovetores é

$$\beta =\{(1,0,1),(0,1,0),(1,0,-1)\}.$$

Na base $\beta$ a matriz de A é diagonal da forma

$$D= \left( \begin{array}{ccc} 3 &0 &0\\ 0& 6 &0 \\ 0 &0 &-2 \end{array}\right).$$

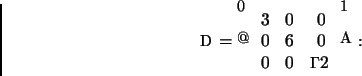
Considerando agora uma base ortonormal de autovetores de A,

$$\gamma =\{(1/\sqrt{2},0,1/\sqrt{2}),(0,1,0),(1/\sqrt{2},0,-1/\sqrt{2})\},$$

temos

$$M= \left( \begin{array}{ccc} 1/\sqrt{2} &0 &1/\sqrt{2}\\ 0& 1 &0 \\ 1/\sqrt{2} &0 &-1/\sqrt{2} \end{array}\right).$$

Como M é ortogonal,

$$M^{-1}=M^t= \left( \begin{array}{ccc} 1/\sqrt{2} &0 &1/\sqrt{... ... 0& 1 &0 \\ 1/\sqrt{2} &0 &-1/\sqrt{2} \end{array}\right)=M.$$

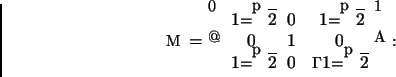
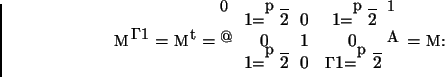
Como A tem determinante não nulo (o produto dos autovetores é diferente de zero) existe A^-1. Temos

A^-1=(MDM^-1)^-1= M D^-1 M^-1=M D^-1 M.

Logo N=N^-1=M. Finalmente,

$$E=D^{-1}= \left( \begin{array}{ccc} 1/3 &0 &0\\ 0& 1/6 &0 \\ 0&0 &-1/2 \end{array}\right).$$