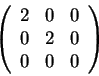P4 de Álgebra Linear I - 2001.2

Data: 3 de dezembro de 2001.

Gabarito

1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque com caneta sua resposta no quadro abaixo. Atenção: responda todos os itens, use "N = não sei" caso você não saiba a resposta. Cada resposta certa vale 0.3, cada resposta errada vale -0.2, cada resposta N vale 0. Respostas confusas e ou rasuradas valerão -0.2.

Itens	V	F	N
1.a		F
1.b		F
1.c	V
1.d		F
1.e	V
1.f		F
1.g	V
1.h		F
1.i		F

1.a) Se $A=\left[ \begin{array}{ll} a & b \\ c & d \end{array}\right]$ e existem vetores u e w tais que Au=2u e Aw=-w, então a soma dos autovalores de A⁶ é igual a 63.

Resposta: Falso. Observe que A²(u)=A(A(u))=A(2u)=2 A(u)=4 u. Repetindo o processo, A⁶(u)=2⁶ u= 64 u. Analogamente, A⁶(w)=(-1)⁶ w= w. Portanto, os autovalores de A⁶ são 64 e 1, e sua soma é 65.

1.b) A distância entre o plano de equação x+y+z=0 e o plano de equação x+y+z=1 é igual a 1.

Resposta: Falso. Considere a reta perpendicular a x+y+z=1 que contém ao ponto (0,0,0), ou seja, (t,t,t). Esta reta intersecta x+y+z=1 quando t=1/3. Logo o ponto de interseção é (1/3,1/3,1/3)e este é o ponto do plano x+y+z=1 mais próximo de x+y+z=0. Logo a distância entre os planos é $(1/9+1/9+1/9)^{1/2}=\sqrt{3}/3\ne 1$.

Outra forma, observe que o ponto (0,0,1)do plano x+y+z=1 está a distância 1 do ponto (0,0,0) do plano x+y+z=0. Logo a distância entre os planos é no máximo 1. E a distância será 1 se, e somente se, o vetor (0,0,1) for normal aos dois planos, o que é falso.

1.c) A reta de equações x=y=z é paralela ao plano de equação 2x-y-z=3.

Resposta: Verdadeiro. Faça o produto escalar $(2,-1,-1)\cdot (1,1,1)$ dos vetores normal ao plano e paralelo à reta, que é zero. Observe também que a reta e o plano são disjuntos, o ponto (0,0,0) da reta não pertence ao plano.

1.d) O volume do paralelepípedo formado pelos vetores $(\frac{1}{\sqrt{2}}, \, 0, \, -\frac{1}{\sqrt{2}})$, $(\frac{1}{\sqrt{2}}, \, 0, \, \frac{1}{\sqrt{2}})$ e $(0,\, 1,\, 0)$é igual a 3.

Resposta: Falso. Os vetores formam uma base ortonormal e seu produto misto é $\pm 1$. Logo o volume é 1.

1.e) É possível encontrar dois vetores u e v não nulos no plano tais que $\parallel u + v \parallel = \parallel u - v \parallel$.

Resposta: Verdadeiro. É suficiente considerar u e v ortogonais:

$$\parallel u + v \parallel^2 = (u+v)\cdot(u+v) = u\cdot u + 2 u \cdot v + v\cdot v= u\cdot u + v\cdot v.$$

Analogamente,

$$\parallel u - v \parallel^2 = (u-v)\cdot (u-v) = u\cdot u - 2 u \cdot v + v\cdot v= u\cdot u + v\cdot v.$$

Logo, como $\parallel u + v \parallel$ e $\parallel u - v \parallel$são não negativos, $\parallel u + v \parallel = \parallel u - v \parallel$

1.f) Se u, v e w são três vetores de ${\mathbb R}^3$perpendiculares entre si, então existem $\alpha$, $\beta$ e $\gamma$números reais não nulos tais que $\alpha u +\beta v +\gamma w = \vec 0$.

Resposta: Falso. Os vetores são linearmente independentes. Por exemplo, para ver que $\alpha$ deve ser necessariamente nulo faça

$$(\alpha u +\beta v +\gamma w)\cdot u= \alpha (u\cdot u) +\bet... ...ot u) +\gamma (w\cdot u)= \alpha (u\cdot u)=\vec 0\cdot u =0.$$

Logo $\alpha=0$. O mesmo argumento fornece $\beta=\gamma=0$.

1.g) Seja T uma matriz ortogonal. Então se $Tv=\vec 0$, então $v=\vec 0$.

Resposta: Verdadeiro. Observe que T conserva módulos, logo se $T(u)=\vec 0$ temos $\vert\vert u\vert\vert=\vert\vert T(u)\vert\vert=\vert\vert\vec 0\vert\vert=0$, logo $u=\vec 0$.

1.h) Se -1, 1 e 1 (isto é, 1 tem multiplicidade 2) são os autovalores de uma matriz A $3\times 3$, então A representa um espelhamento com relação a um plano.

Resposta: Falso. Observe que os autovetores não têm que ser necessariamente ortogonais. Por exemplo:

$$\left( \begin{array}{ccc} 1 &0 & 0\\ 1 &1 &0\\ 1 & 1 & -1 \end{array}\right)$$

satisfaz as hipóteses do enunciado é não é espelhamento.

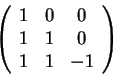
1.i) Se R é uma rotação de 90^o em ${\mathbb R}^3$ e se unão pertence ao eixo de rotação, então $u \cdot Ru =0$, isto é, u e R(u) são ortogonais.

Resposta: Falso. Considere a rotação de $\pi/2$ graus e eixo Z

$$\left( \begin{array}{ccc} 0 &-1 & 0\\ 1 &0 &0\\ 0 & 0 & 1 \end{array}\right).$$

O vetor (1,1,1) se transforma em (-1,1,1) e estes dois vetores não são ortogonais (seu produto escalar vale 1).

2) Considere as retas r e s definidas pelas equações:

$$r:\left\{ \begin{array}{cccccccccc} x & + & y & + & z & = & 0 &\\ x & - & y & & & = & 1 &\\ \end{array}\right.$$

$$s:\left\{ \begin{array}{cccccccccc} x & = & 0 & + & t &\\ ... ... & -1 & + & 2t &\\ \end{array}\right. \quad t\in \mathbb{R} .$$

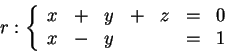
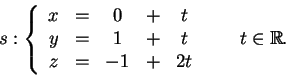
2.a) Determine uma equação paramétrica de r.

2.b) Determine uma equação cartesiana de s, isto é, escreva s como interseção de dois planos dados em equações cartesianas.

2.c) Estude a posição relativa de r e s.

2.d) Se a sua resposta no item (2.c) foi reversas ou paralelas calcule a distância entre r e s, e se foi se intersectam determine a equação cartesiana do plano que contém as retas r e s.

Resposta: Para o item (a) uma forma é resolver os sistema. Temos, x=y+1 e z=-2y -1. Escolhendo y como parâmetro temos

$$x=t+1, \quad y=t, \quad z= -2t -1, \quad t\in \mathbb{R} .$$

Outra forma é calcular o vetor diretor v da reta, que é ortogonal aos vetores normais aos dois planos. Logo v é paralelo a $(1,1,1)\times (1,-1,0)=(1,1,-2)$. Agora é suficiente determinar um ponto comum aos dois planos: o ponto (1,0,-1).

Para o item (b) é suficiente encontrar dois planos não paralelos contendo a s. Os vetores normais destes planos devem ser ortogonais ao vetor diretor da reta. Ou seja, se (a,b,c) é o vetor normal do plano então

a+b+2c=0.

Um plano é da forma (por exemplo) x-y=d e outro $2x-z=d^\prime$ onde d e $d^\prime$ sào dados pela condição (0,1,-1) pertencer aos planos. Logo,

$$x-y=-1,\quad 2x-z=1.$$

As retas r e s têm vetores diretores não paralelos. Logo ou são reversas ou se intersetam. Considere o ponto P=(1,0,-1) de r e Q=(0,1,-1) de s. Considere o vetor QP=(1,-1,0) e os vetores diretores (1,1,-2) de r e (1,1,2) de s. Para as retas serem reversas é necessário e suficiente que

$$(1,-1,0)\cdot [ (1,1,-2)\times(1,1,2)]\ne 0.$$

Como

$$(1,-1,0)\cdot [(1,1,-2)\times(1,1,2)]=(1,-1,0)\cdot (4,-4,0)=8,$$

as retas são reversas.

A distância entre as retas é

$$\frac{8}{\vert\vert(1,1,-2)\times(1,1,2)\vert\vert}= \frac{8}... ...)\vert\vert}= \frac{8}{4\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}.$$

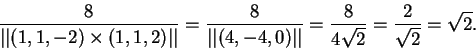
3) Considere $\beta=\{(1,1,0), (1,0,1), (0,1,1), (0,1,0)\}$.

3.a) Estude se $\beta$ é uma base de ${\mathbb R}^3$.

3.b) Considere uma transformação linear A de ${\mathbb R}^3$em ${\mathbb R}^3$ verificando

$$A(1,1,0)=(1,0,1), \quad A(1,0,1)=(0,1,1), \quad A(0,1,1)=(1,0,1).$$

Estude se A é ortogonal.

3.c) Determine a matriz de A na base canônica.

3.d) Determine um autovalor e um autovetor (associado ao autovalor encontrado) de A.

3.e) Encontre uma base onde a matriz de A é da forma

$$\left( \begin{array}{llll} 0 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right) \ .$$

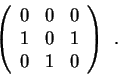
Resposta: Obviamente $\beta$ não é uma base: uma base de ${\mathbb R}^3$tem três vetores (que são l.i.) (quatro vetores de ${\mathbb R}^3$ nunca são l.i.).

A transformação A não é ortogonal. Para ser ortogonal deve conservar módulos. Observe que

$$A(1,0,-1)= A(1,1,0)- A(0,1,1)=(1,0,1)-(1,0,1)=\vec 0.$$

Como (1,0,-1) tem módulo $\sqrt{2}$ a matriz não é ortogonal.

Outra forma, mais trabalhosa, e determinar a matriz de A na base canônica e ver que não é ortogonal. Isso será feito no próximo item.

Para determinar A na base canônica devemos determinar A(1,0,0), A(0,1,0) e A(0,0,1). Temos

A(0,1,-1)=A(1,1,0)-A(1,0,1)= (1,0,1)-(0,1,1)=(1,-1,0).

Logo

A(0,2,0)=A(0,1,-1)+A(0,1,1)=(1,-1,0)+(1,0,1)=(2,-1,1).

Portanto,

A(0,1,0)=(1,-1/2,1/2).

Finalmente,

A(1,0,0)=A(1,1,0)-A(0,1,1)=(1,0,1) -(1,-1/2,1/2)=(0,1/2,1/2)

e

A(0,0,1)=A(0,1,1)-A(0,1,0)=(1,0,1) -(1,-1/2,1/2)=(0,1/2,1/2)

Logo a matriz de A na base canônica é

$$[A]= \left( \begin{array}{ccc} 0 & 1 & 0 \\ 1/2 &-1/2 & 1/2\\ 1/2 &1/2 & 1/2 \end{array}\right).$$

Verifique que os resultados estão certos (aplique a matriz aos vetores (1,1,0), (0,1,1) e (1,0,1) e veja o resultado).

Para o último item considere a base

$$\gamma=\{u=(1,1,0), v=(1,0,1), w=(0,1,1)\}.$$

Observe que A(u)=v, A(v)=w e A(w)=v. Logo a matriz de A na base $\gamma$ é a matriz do problema.

4) Considere a matriz

$$P=\left( \begin{array}{ccc} 2/3 & a & b \\ -1/3 & 2/3 & c \\ -1/3 & -1/3 & d \end{array}\right) \ .$$

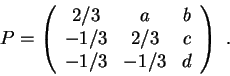
4.a) Determine a, b, c e d para que P represente uma projeção ortogonal em um plano. Determine a equação do plano de projeção.

4.b) Considere agora a matriz

$$A= \left( \begin{array}{ccc} 1/\sqrt{2} & 1/\sqrt{6} &1/\sqrt... ...6}\\ 1/\sqrt{3} & -1/\sqrt{3}& 1/\sqrt{3} \end{array}\right).$$

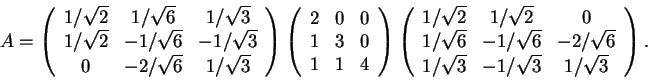
Determine os autovalores de A.

4.c) Finalmente considere a matriz

$$B= \left( \begin{array}{ccc} 1/\sqrt{2} & 1/\sqrt{6} &1/\sqrt... ...6}\\ 1/\sqrt{3} & -1/\sqrt{3}& 1/\sqrt{3} \end{array}\right).$$

Interprete geometricamente B. Nos casos envolvendo projeções determine a reta ou plano de projeção, nos casos envolvendo espelhamentos determine o plano ou reta de espelhamento, e nos casos envolvendo rotações determine o ângulo e o eixo de rotação.

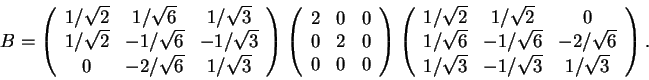
Resposta: A matriz P deve ser simétrica. Portanto, a=-1/3=b=c. Para determinar d use que a matriz deve ter traço dois, pois se trata de uma projeção em um plano que tem autovalores 1 (de multiplicidade 2) e 0, logo o traço é 1+1+0=2. Logo 2/3+2/3+d=2, d=2/3. De outra forma: d é dado pelo fato do determinante ser zero. De outra forma, d é dado pelo fato do vetor (-1/3,-1/3,d) pertencer ao plano paralelo a (2/3, -1/3,-1/3) e (-1/3,2/3,-1/3).

Para determinar o plano observe que P(i)=(2/3, -1/3,-1/3) e P(j)=(-1/3, 2/3,-1/3) são vetores paralelos ao plano de projeção. Logo o vetor norma é paralelo a $(2,-1,-1)\times (-1,2,-1)=(3,3,3)$. Logo o plano de projeção é x+y+z=0.

Observe que a matriz A é semelhante à matriz triangular

$$T=\left( \begin{array}{ccc} 2 & 0 &0\\ 1 & 3& 0\\ 1 & 1& 4 \end{array}\right),$$

pois A=P T P^-1 onde P é a matriz ortogonal

$$\left( \begin{array}{ccc} 1/\sqrt{2} & 1/\sqrt{6} &1/\sqrt{3}... ...-1/\sqrt{3}\\ 0 & -2/\sqrt{6}& 1/\sqrt{3} \end{array}\right).$$

Como matrizes semelhantes têm os mesmos autovalores é suficiente determinar os autovalores de T. Observe que os autovalores de uma matriz triangular são os elementos da diagonal, logo os autovalores de T (e portanto os de A) são 2, 3 e 4.

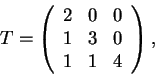
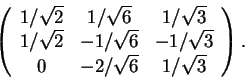
Para o último item considere a base ortonormal

$$\beta=\{ (1/\sqrt{2}, 1/\sqrt{2},0), (1/\sqrt{6}, -1/\sqrt{6}, -2/\sqrt{6}), ( 1/\sqrt{3}, -1/\sqrt{3}, 1/\sqrt{3})\}.$$

A matriz de B na base $\beta$ é

$$\left( \begin{array}{ccc} 2 & 0 &0\\ 0 & 2& 0\\ 0 & 0& 0 \end{array}\right)$$

que representa uma projeção no plano paralelo aos vetores $(1/\sqrt{2}, 1/\sqrt{2},0)$ e $(1/\sqrt{6}, -1/\sqrt{6}, -2/\sqrt{6})$seguida de uma multiplicação por 2. Por construção o vetor normal de tal plano é (1,-1,1), logo o plano de projeção é x-y+z=0.