P1 de Álgebra Linear I - 2001.2

Sábado, 15 de setembro de 2001.

Gabarito

1) Sejam u e v vetores unitários de $\mathbb{R} ^3$.

a) Suponha que $(u+v)\cdot (u+v)= (u-v)\cdot (u-v)$. Calcule o ângulo formado pelos vetores u e v.

b) Suponha que $(u+v)\cdot (u+v)= (u-v)\cdot (u-v)+2\, \sqrt{2}$. Calcule o ângulo formado pelos vetores u e v.

c) Suponha que $u\times v=\bar 0=(0,0,0)$. Calcule $\vert u\cdot v\vert$.

d) Considere um vetor n. Sabendo que $n\cdot (u\times v)=5$, calcule $v\cdot (n\times u)$

e) Considere um vetor não nulo n. Calcule $u\cdot (n\times n)$.

Resposta:

a) Pelas propriedades do produto escalar, $(u+v)\cdot (u+v)= u\cdot (u+v) + v\cdot (u+v)= u\cdot u + u\cdot v + v\cdot u + v\cdot v$. Como u e v são vetores unitários, $u\cdot u = v\cdot v=1$. Lembre também que $u\cdot v= v\cdot u$. Logo,

$$(u+v)\cdot (u+v)=2 + 2 \, u\cdot v.$$

Analogamente, $(u-v)\cdot (u-v)= u\cdot (u-v) - v\cdot (u-v)= u\cdot u - u\cdot v - v\cdot u + v\cdot v$. Como u e v são vetores unitários, $u\cdot u = v\cdot v=1$. Lembre também que $u\cdot v= v\cdot u$. Logo,

$$(u-v)\cdot (u-v)=2 - 2 \, u\cdot v.$$

Usando que $(u+v)\cdot (u+v)= (u-v)\cdot (u-v)$, temos

$$2 + 2 u\cdot v= 2 -2 \, u\cdot v, \quad 4\, u\cdot v=0, \quad u\cdot v=0$$

Como $u\cdot v=\vert u\vert\vert v\vert\cos \alpha= \cos \alpha$, onde $\alpha$ é o ângulo formado pelos vetores, temos que $\cos \alpha=0$, e os vetores são ortogonais (ângulo $\pi/2$ ou $-\pi/2$).

b) Pelos cálculos já feitos, $(u+v)\cdot (u+v)= 2 + 2\, u\cdot v$e $(u-v)\cdot (u-v)= 2 - 2\, u\cdot v$. Logo a igualdade pode ser reescrita como

$$2 + 2 u\cdot v = 2 - 2\, u \cdot v + 2\sqrt{2}, \quad 2 u\cdot v = - 2 \,u \cdot v + 2\sqrt{2}, \quad 4 u\cdot v =2\sqrt{2}.$$

Isto é,

$$u\cdot v =\sqrt{2}/2.$$

Novamente, $u\cdot v=\vert u\vert\vert v\vert\cos \alpha=\cos \alpha=\sqrt{2}/2$, onde $\alpha$ é o ângulo formado pelos vetores, temos que $\cos \alpha=\sqrt{2}/2$, e os vetores formão um ângulo de $\pm \pi/4$.

c) Observe que $\vert u\times v\vert=\vert u\vert\vert v\vert\mbox{sen}\alpha= \mbox{sen}\alpha=0$, onde $\alpha$ é o ângulo formado pelos vetores. Logo $\alpha =\pi$ ou $\alpha =0$, e os vetores são paralelos. Portanto, $\vert u\cdot v\vert=\vert u\vert\vert v\vert\vert\cos (0)=1$.

d) Pelas propriedades do produto vetorial:

$$v\cdot (n\times u)=- n\cdot (v\times u)= -(-n \cdot (u\times v)) = n\cdot (u\times v)=5.$$

e) 0bserve $n\times n=\bar 0$, pois $\vert n\times n\vert =\vert n\vert\vert n\vert \mbox{sen}(0)=0$. Logo $u \cdot (n\times n)=u \cdot \bar 0=0$.

2) Considere o plano $\pi\colon x-y+z=2$.

a) Determine a equação cartesiana do plano $\rho$ paralelo a $\pi$ que contém a origem.

b) Determine as equações paramétricas de $\pi$.

c) Calcule a distância entre os planos $\pi$ e $\rho$.

d) Calcule o ponto de $\rho$ mais próximo do ponto (1,0,1) de $\pi$.

e) Determine um triângulo retângulo com dois vértices em $\pi$ e um vértice em $\rho$.

Resposta:

a) O vetor normal de $\pi$ é (1,-1,1). Como $\rho$ é paralelo a $\pi$, $\pi$ e $\rho$ têm o mesmo vetor normal, logo é da forma, x-y+z=d. Para determinar d usamos que (0,0,0) pertence ao plano $\rho$, logo d=0 e $\rho\colon x-y+z=0$.

b) Para determinar as equações paramétricas de $\pi$ devemos encontrar um ponto P de $\pi$ e dois vetores u e v paralelos a este plano, isto é, ortogonais a (1,-1,1), e não paralelos entre si.

Podemos tomar P=(1,0,1), u=(1,1,0) (verifica $u\cdot n=0$) e v=(0,1,1) (verifica $v\cdot n=0$).

Uma equação paramétrica é

$$x=1+t,\quad y=0+t+s, \quad z=1+s, \qquad t,s\in \mathbb{R} .$$

Observe que existem outras equações paramétricas de $\pi$: o ponto Q=(2,1,1) pertence a $\pi$ e os vetores (1,2,1) e (1,7,6) são paralelos a $\pi$ (veja que o produto escalar destes vetores por n é zero). Logo, outra equação paramétrica de $\pi$ é

$$x=2+t+s,\quad y=2+2t+7s, \quad z=1+t+6s, \qquad t,s\in \mathbb{R} .$$

Outra forma de resolver a questão é escolher x e y como parâmetros (t e s) e escrever z, em função destes parâmetros: x-y+z=2, logo t-s+z=2, z=2-t+s,

$$x=t,\quad y=s, \quad z=2-t+s, \qquad t,s\in \mathbb{R} .$$

c) A distância entre os planos é igual a distância de qualquer ponto Q (por exemplo a origem) de $\rho$ a $\pi$. Calcularemos esta distância usando dois métodos.

Método 1: Considere o ponto P=(1,0,1) de $\pi$. A distância é o módulo da projeção do vetor $\overline{QP}=(1,0,1)$ no vetor normal do plano $\pi$, $m=(1/\sqrt{3},-1/\sqrt{3},1/\sqrt{3})$. O vetor projeção é

$$\begin{array}{ll} &[(1,0,1)\cdot (1/\sqrt{3}, -1/\sqrt{3},1/\... .../\sqrt{3}, -1/\sqrt{3},1/\sqrt{3})= (2/3,-2/3,2/3). \end{array}$$

Este vetor tem módulo $\sqrt{12}/3=2/\sqrt{3}$.

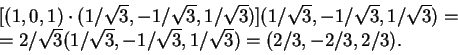
Método 2: Calcularemos o ponto T de interseção do plano $\pi$ e da reta r perperdicular a $\pi$ contendo $(0,0,0)\in \rho$. A distância é comprimento do segmento $\overline{0T}$.

A reta r é (t,-t,t), $t\in \mathbb{R}$. Logo para obter o ponto de interseção resolvemos,

$$t-(-t) + t=2, \quad t=2/3, \quad T=(2/3,-2/3,2/3).$$

Observe agora que o tamanho do segmento já foi calculado no item anterior.

d) Para calcular o ponto mais próximo de A=(1,0,1) do plano $\rho$consideramos a interseção da reta s perpendicular a $\rho$ contendo A e o próprio plano $\rho$. A reta s tem equação, (1+t,-t,1+t), $t\in \mathbb{R}$. O ponto de interseção de s e $\rho$ é obtido resolvendo

$$(1+t)-(-t) (1+t)=0,\quad 3t=-2, \quad t=-2/3.$$

Logo o ponto é (1/3,2/3,1/3).

Existe outro método diferente. É suficiente observar que o vetor projeção de $\overline{QP}$ em (1,-1,1) é (2/3,-2/3,2/3). Portanto, dado qualquer ponto B de $\pi$ se verifica que $C=B-(2/3,-2/3,2/3)\in \rho$ e que C é o ponto de $\rho$ mais próximo de B. No nosso caso, (1,0,1)-(2/3,-2/3,2/3)= (1/3,-2/3,1/3).

e) Observe que o triângulo com vértices $B=(1/3,2/3,1/3)\in \rho$, $A=(1,0,1)\in \pi$ e C (onde C é qualquer ponto de $\pi$, $C\ne A$) é um triângulo retângulo: o vetor $\overline{AB}$ é paralelo ao vetor normal do plano $\pi$ e o vetor $\overline{AC}$ é paralelo a $\pi$, logo ortogonal a $\overline{AB}$. Portanto, escolhemos qualquer ponto de $\pi$ diferente de (1,0,1), por exemplo (2,2,2).

3) Considere a reta r₁ dada como intersecção dos planos x-z=1 e x-y=1. Seja a reta $r_2\colon (t,-t,t)$, $t\in \mathbb{R}$.

a) Determine um vetor diretor de r₁.

b) Determine uma equação paramétrica de r₁.

c) Escreva a reta r₂ como intersecção de dois planos $\pi$ e $\rho$ dados em equações paramétricas.

d) Calcule a distância entre as retas r₁ e r₂.

e) Determine a posição relativa das retas r₁ e r₂.

Resposta:

a) Sejam n=(1,0,-1) e m=(1,-1,0) os vetores normais dos planos que definem r₁. O vetor diretor de r₁ é $v=n\times m=(1,0,-1)\times (1,-1,0)=(-1,-1,-1)$. Logo podemos tomar como vetor diretor (1,1,1).

b) Existem dois métodos. Primeiro é encontrar um ponto de r₁, por exemplo (1,0,0), e a equação é (1+t,t,t), $t\in \mathbb{R}$.

Outro método é resolver o sistema. Temos z=x-1 e y=x-1. Escolhendo x como parâmetro temos, (t,-1+t,-1+t), $t\in \mathbb{R}$. Observe que as duas equações paramétricas definem a mesma reta.

Outra forma de resolver os itens anteriores é a seguinte: resolvemos o sistema

$$x-z=1, \quad x-y=1,$$

temos

$$z=x-1, \quad y=x-1.$$

Tomando x como parâmetro temos (t,t-1,t-1), $t\in \mathbb{R}$. Assim temos a equação paramétrica e sabemos que o vetor diretor é (1,1,1).

c) Devemos escolher dois planos $\rho$ e $\pi$ que não sejam paralelos e contenham a r₂. Como o ponto $A=(1,1,1)\not\in r_2$, o ponto A e r₂ determinam um plano que contém a r₂. Dois vetores paralelos a este plano são $\overline{0A}=(1,1,1)$e (1,-1,1), e um ponto é a origem, logo a equação paramétrica de $\pi$ é

$$x=s+t, \quad y=s-t, \quad z=s+t, \quad s, t\in \mathbb{R} .$$

Para determinar o plano $\rho$ escolhemos um ponto B que não pertença a $\pi$, por exemplo, B=(1,0,0). Observe que se $B\in \pi$ então

$$1=s+t, \quad 0=s-t, \quad 0=s+t,$$

logo, das duas últimas equações, s=t e 2t=0, logo s=t=0, e $1\ne 0+0$.

Raciocinanco como no caso de $\pi$, Como $B=(1,0,0)\not\in r_2$, o ponto B e r₂ determinam um plano que contém a r₂. Dois vetores paralelos a este plano são $\overline{0B}(1,0,0)$e (1,-1,1), e um ponto é a origem, logo a equação paramétrica de $\pi$ é

$$x=s+t, \quad y=-t, \quad z=+t, \quad s, t\in \mathbb{R} .$$

d) Para calcular a distância entre as retas escolhemos um ponto P=(1,0,0) de r₁, um ponto Q=(0,0,0) de r₂ e os vetores diretores das duas retas, (1,1,1) e (1,-1,1). Sabemos que a distância d é dada por

$$d=\frac{\vert\overline{OP} \cdot ((1,1,1)\times (1,-1,1))\ver... ... (1,-1,1))\vert} {\vert\vert(1,1,1)\times (1,-1,1)\vert\vert}.$$

Temos

$$(1,1,1)\times (1,-1,1)=(2,0,-2), \quad \vert\vert(2,0,-2)\vert\vert=\sqrt{2^2+0^2+2^2}=\sqrt{8}=2\sqrt{2}.$$

Também,

$$(1,0,0)\cdot (2,0,-2)=2.$$

Logo a distância é $d=1/\sqrt{2}=\sqrt{2}/2$

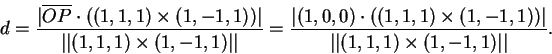
e) As retas são reversas: não são paralelas (vetores diretores não paralelos) e a distância é não nula.

4) Considere os planos

$$\pi_1\colon x+y-z=1,\quad \pi_2\colon 2x+y+z=2,\quad \pi_3\colon 2x+2y-2z=2,\quad \pi_4\colon x+2z=3,$$

e a reta

$$r\colon (t,2t,3t),\quad t\in \mathbb R.$$

a) Determine a posição relativa de $\pi_1$ e $\pi_2$.

b) Determine a posição relativa de $\pi_1$ e $\pi_3$.

c) Determine a posição relativa de $\pi_1$, $\pi_2$ e $\pi_4$.

d) Determine a posição relativa de $\pi_1$ e r.

Resposta:

a) O vetor normal n₁ de $\pi_1$ é (1,1,-1). O vetor normal n₂ de $\pi_2$ é (2,1, 1). Como estes vetores não são paralelos (veja que $n_1\ne \sigma n_2$ para todo $\sigma\in \mathbb{R}$ou que $n_1\times n_2\ne \bar 0$), os planos se intersectam ao longo de uma reta r.

b) O vetor normal n₁ de $\pi_1$ é (1,1,-1). O vetor normal n₃ de $\pi_3$ é (2,2, -2). Observe que n₂=2 n₁. Logo os vetores normais são paralelos e os planos também. Falta ver se são iguais (mesmo plano) ou disjuntos. Como o ponto (1,0,0) pertence aos dois planos, estes são iguais. Observe que a equação de $\pi_3$ é obtida multiplicando por 2 a equação de $\pi_1$.

c) O vetor normal n₁ de $\pi_1$ é (1,1,-1). O vetor normal n₂ de $\pi_2$ é (2,1, 1). O vetor normal n₄ de $\pi_4$ é (1,0,2).

Observe que n₁ não é paralelo a n₂, que n₁ não é paralelo a n₄, e que n₂ não é paralelo a n₄. Logo nenhum plano é paralelo ao outro.

Calculemos $n_1\cdot (n_2\times n_4)$,

$$(1,1,-1)\cdot [(2,1,1)\times(1,0,2)]=(1,1,-1)\cdot (2,-3,-1)=2-3+1=0.$$

Logo os vetores são coplanares. Existem duas possibilidades:

(I) se o sistema admite solução, os planos se intersectam ao longo de uma reta,

(II) se o sistema não admite solução, os planos se intersectam dois a dois ao longo de três retas paralelas entre si.

Para ver se o sistema tem solução escalonaremos os sistema, considerando a segunda equação menos duas vezes a primeira e a terceira menos a primeira,

$$x+y-z=2, \quad -y +3z=0, \quad -y +3z=2.$$

Considerando, a terceira menos a segunda, temos,

$$x+y-z=2, \quad -y +3z=0, \quad 0=2.$$

Logo o sistema não tem solução, e a resposta é (II).

Outra forma de resolver a questão é a seguinte: O determinante cujas linhas são os vetores normais aos planos é

$$\left\vert \begin{array}{ccc} 1 & 1 &-1\\ 2 & 1& 1\\ 1 &0 &2 \end{array}\right\vert= 1( 2-0) - 1(4-1) -1 (0 -1)= 2-3+1=0.$$

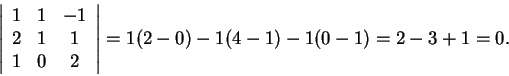
Por outra parte o determinante obtido susbtituindo a primeira linha pelos coeficientes sem incógnitas é:

$$\left\vert \begin{array}{ccc} 1 & 1 &-1\\ 2 & 1& 1\\ 3 &0 &2 \end{array}\right\vert= 1( 2-0) - 1(4-3) -1 (0 -3)= 2-1+3\ne 0.$$

Logo o sistema não admite solução, e portanto os planos não tem intersecção común.

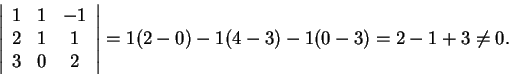
Por outra parte, como já vimos, os planos não são paralelos, logo se intersectam dois a dois em retas paralelas.

d) O vetor normal n₁ de $\pi_1$ é (1,1,-1). O vetor vetor diretor v de r é (1,2,3). Observe que $v\cdot n_1=1+2-3=0$. Logo n₁ e v são ortogonais. Isto significa que r e $\pi_1$ são paralelos. Como a origem $(0,0,0)\in r$ e não pertence a $\pi_1$, a reta e o plano são paralelos e disjuntos.