No Title

P4 de Álgebra Linear I - 2002.1

Data: 14 de junho de 2002.

to to 0.7Nome: Matrícula: to to 0.7Assinatura: Turma:

Questão	Valor	Nota	Revis.
1	2.5
2a	0.5
2b	0.5
2c	0.5
2d	0.5
2e	0.5
3a	0.5
3b	0.5
3c	0.5
3d	0.5
3e	0.5
4a	0.5
4b	0.5
4c	0.5
4d	0.5
4e	0.5
Total	10.0

Instruções:

Não é permitido usar calculadora. Desligue o celular.
É proibido desgrampear a prova. Prova com folhas faltando ou rasuradas terá nota zero.
Nas questões 2, 3 e 4 justifique cuidadosamente todas as respostas de forma completa, ordenada e coerente. Escreva de forma clara e legível.
Nas questões 2, 3 e 4 da prova não haverá pontuação menor que 0.5 - Verifique cuidadosamente suas respostas.
Faça a prova na sua turma.

Marque no quadro as respostas da primeira questão. Não é necessário justificar esta questão.

ATENÇÃ0: resposta errada vale ponto negativo!, a questão pode ter nota negativa!

Para uso exclusivo do professor	*****	*****
Certas:	$\times$ 0.3
Erradas:	$\times$ -0.2
*****	Total

1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque com caneta sua resposta no quadro abaixo. Atenção: responda todos os itens, use "N = não sei" caso você não saiba a resposta. Cada resposta certa vale 0.3, cada resposta errada vale -0.2, cada resposta N vale 0. Respostas confusas e ou rasuradas valerão -0.2.

Itens	V	F	N
1.a
1.b
1.c
1.d
1.e
1.f
1.g
1.h
1.i

1.a) Considere as retas de equações paramétricas

$\begin{displaymath}r=(p_1+tv_1, p_2+tv_2, p_3+tv_3), \quad \mbox{e} \quad s=(q_1+tw_1, q_2+tw_2, q_3+tw_3), \quad t\in \mathbb{R} . \end{displaymath}$

Suponha que

$\begin{displaymath}(p_1-q_1,p_2-q_2,p_3-q_3)\cdot (v_1,v_2,v_3) \times (w_1,w_2,w_3)=0. \end{displaymath}$

Então as retas se interceptam em um ponto.

1.b) A multiplicação de duas matrizes ortogonais é uma matriz ortogonal.

1.c) Sejam A uma matriz $3\times 3$ cujo polinômio caraterístico é

$\begin{displaymath}p(\lambda)=-(\lambda-1)^2(\lambda-2). \end{displaymath}$

Então A não é diagonalizável.

1.d) Seja A uma matriz $2\times 2$ ortogonal e simétrica. Então A representa um espelhamento.

1.e) Considere o plano $\pi$ de equação cartesiana ax+by+cz=d e a reta r=(p₁+tv₁, p₂+tv₂, p₃+tv₃). Suponha que $(a,b,c)\cdot (v_1,v_2,v_3)=0$ . Então a reta e o plano têm exatamente um ponto de interseção.

1.f) Considere a matriz

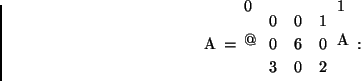
$\begin{displaymath}A= \left( \begin{array}{ccc} 0 &0 &1\\ 0& 6 &0 \\ 3 &0 &2 \end{array}\right). \end{displaymath}$

Os autovalores de A são 0, 6 e 2.

1.g) Considere uma transformação linear P de $\mathbb{R} ^3$ tal que $P^2=P\circ P=P$ . Então P é uma projeção ortogonal.

1.h) O produto de duas matrizes inversíveis é uma matriz inversível.

1.i) Os vetores $\{(1,1,1), (1,0,-1), (1,-2,1)\}$ formam uma base ortonormal.

2) Considere o plano x+y+z=0, o ponto p=(1,1,1) e as retas r₁=(t,1-t,t) e r₂=(1-t, 1+t,t), $t\in \mathbb{R}$ . Determine

: (2.a) A equação da reta r que contém o ponto p e é perpendicular a $\pi$ .
: (2.b) A equação do plano que contém o ponto p e é paralelo a r₁ e r₂.
: (2.c) A distância entre as retas r₁ e r₂.
: (2.d) A posição relativa das retas r₁ e r₂.
: (2.e) A posição relativa da reta r₂ e o plano $\pi$ .

3) Considere a projeção ortogonal P no plano 2x+2y+2z=0 e a projeção Q no plano x+y+z=0 na direção da reta (t,-t,0), $t\in \mathbb{R}$ .

: (3.a) Determine os autovalores de P e de Q.
: (3.b) Determine bases de autovetores de P e de Q.
: (3.c) Escreva P da forma P=MD M^-1, onde D é uma matriz diagonal. Determine explicitamente M e M^-1.
: (3.d) Escreva Q da forma Q=NE N^-1, onde E é diagonal. Determine explicitamente N.
: (3.e) Determine a relação entre as transformações $Q\circ P$ e P.

4) Considere a matriz

$\begin{displaymath}A= \left( \begin{array}{ccc} 1 &0 &3\\ 0& 6 &0 \\ 3 &0 &1 \end{array}\right). \end{displaymath}$

: (4.a) Determine os autovalores de A.
: (4.b) Determine uma base de autovetores A.
: (4.c) Determine uma forma diagonal D de A.
: (4.d) Escreva A da forma A=MD M^-1 onde D é uma matriz diagonal. Determine explicitamente M e M^-1.
: (4.e) Escreva, caso exista, a matriz A^-1 inversa de A da forma A^-1=NE N^-1, onde E é uma matriz diagonal. Determine explicitamente N e N^-1.

About this document ...

Next: About this document ...

Lorenzo J. Diaz
2002-07-03