P1 de Álgebra Linear I - 2002.1

Data: 27 de março de 2001.

to to 0.7Nome:  Matrícula: to to 0.7Assinatura: Turma:

Questão	Valor	Nota	Revis.
1	2.5
2a	0.5
2b	0.5
2c	0.5
2d	0.5
2e	0.5
3a	0.5
3b	1.0
3c	1.0
4a	0.5
4b	0.5
4c	0.5
4d	0.5
4e	0.5
Total	10.5

Instruções:

• Não é permitido usar calculadora. Mantenha o celular desligado.

• É proibido desgrampear a prova. Prova com folhas faltando ou rasuradas terá nota zero.

• Nas questões 2, 3 e 4 justifique cuidadosamente todas as respostas de forma completa, ordenada e coerente. Escreva de forma clara e legível.
• Nas questões 2, 3 e 4 da prova não haverá pontuação menor que 0.5 - Verifique cuidadosamente suas respostas.
• Faça a prova na sua turma.

Marque no quadro as respostas da primeira questão. Não é necessário justificar esta questão.

ATENÇÃ0: resposta errada vale ponto negativo!, a questão pode ter nota negativa!

Para uso exclusivo do professor	*****	*****
Certas:	$\times$ 0.3
Erradas:	$\times$ -0.2
*****	Total

1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque com caneta sua resposta no quadro abaixo. Atenção: responda todos os itens, use "N = não sei" caso você não saiba a resposta. Cada resposta certa vale 0.3, cada resposta errada vale -0.2, cada resposta N vale 0. Respostas confusas e ou rasuradas valerão -0.2.

Itens	V	F	N
1.a
1.b
1.c
1.d
1.e
1.f
1.g
1.h
1.i

1.a) Para todo par de vetores u e w de $\mathbb{R} ^3$ vale o seguinte raciocínio:

$$w\times (u\times w)=-w\times (w \times u)= (-w\times w)\times u=\bar 0\times u=\bar 0$$

1.b) Considere vetores v, y e w de $\mathbb{R} ^3$ tais que $y\cdot (v\times w)=1$. Então $w\cdot (v\times y)=1$.

1.c) Considere vetores v, y e w de $\mathbb{R} ^3$ tais que $y\cdot (v\times w)=0$. Então y é ortogonal a w.

1.d) Existem dois planos $\pi$ e $\rho$ de $\mathbb{R} ^3$ cuja interseção consiste em um único ponto.

1.e) Considere vetores y,v e w de $\mathbb{R} ^3$ tais que $y\cdot v=0$ e $w\cdot v=0$. Então $y\cdot w=0$.

1.f) Considere vetores w e v de $\mathbb{R} ^3$. Se $w\times v=0$então o valor absoluto de $w\cdot v$ é $\vert w\vert\, \vert v\vert$.

1.g) Considere o sistema

$$a_1x+b_1y+c_1z=d_1, \quad a_2x+b_2y+c_2z=d_2, \quad a_3x+b_3y+c_3z=d_3.$$

Suponha que

$$\left\vert \begin{array}{ccc} a_1 &b_1 &c_1\\ a_2 &b_2 &c_2\\ a_3 &b_3 &c_3 \end{array}\right\vert= 0.$$

Então o sistema não admite solução.

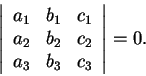
1.h) Considere vetores y,v e w de $\mathbb{R} ^3$. Então

$$(y+v)\cdot (w\times v)= y\cdot (w\times v).$$

1.i) Considere a reta r que contém o ponto P=(p₁,p₂,p₃) e é paralela ao vetor v, e a reta sque contém ao ponto Q=(q₁,q₂,q₃) e é paralela ao vetor w. Seja $\overline{PQ}=(q_1-p_1,q_2-p_2,q_3-p_3)$. Suponha que $\overline{PQ}\cdot (v\times w)=0$. Então a distância entre as retas é zero.

2) Considere a reta r definida pela interseção dos planos $\pi$ e $\rho$,

$$\pi\colon x + 2y + z = 1, \quad \rho \colon -x + y - z = 1.$$

2.a) Determine um vetor diretor da reta r.

2.b) Determine uma equação paramétrica de r.

2.c) Encontre um terceiro plano $\tau$ (diferente de $\pi$ e $\rho$) que contenha a r (isto é, $\tau \cap \pi \cap \rho$ é igual à reta r).

2.d) Determine a equação cartesiana do plano $\alpha$ que contém a reta r e o ponto (1,2,1).

2.e) Determine a equação cartesiana do plano $\beta$ perpendicular a r contendo o ponto (1,2,1).

3) Considere a reta r de equação cartesiana

$$x+2y+z=4, \quad x-z=0$$

e a reta sde equações paramétricas $(1-2t, t, 1+2t), \, t\in \mathbb{R}$.

3.a) Determine uma equação paramétrica de r.

3.b) Determine a posição relativa das retas r e s(concorrentes, reversas, paralelas, iguais).

3.c) Calcule a distância entre r e s.

4) Considere o plano $\pi\colon x+2y-z=1$.

4.a) Determine a equação cartesiana do plano $\rho$ paralelo a $\pi$ que contém a origem.

4.a) Calcule a distância entre $\rho$ e $\pi$.

4.c) Determine a equação cartesiana do plano $\tau$ perpendicular a $\pi$ que contém os pontos (1,0,0) e (0,0,-1).

4.d) Calcule o ponto do plano $\rho$ mais próximo do ponto (1,0,0).

4.e) Ache um ponto X no plano $\rho$ da forma (x,0,z) tal que os pontos P=(1,0,0), Q=(0,0,-1) (P,Q no plano $\pi$) determinem um triângulo retângulo cujos catetos são PQ e QX.