P3 de Álgebra Linear I - 2001.1

Data: 20 de junho de 2001.

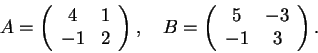
1) Considere as matrizes

$$A= \left( \begin{array}{cc} 4 & 1 \\ -1 & 2 \end{array}\... ...t( \begin{array}{cc} 5 & -3 \\ -1 & 3 \end{array}\right).$$

a) Determine os autovalores e autovetores das matrizes A e B. (0.5+0.5).

b) Estude se estas matrizes são diagonalizáveis. (0.5).

c) Escreva as matrizes diagonalizáveis do item anterior na forma R D R^-1 onde D é uma matriz diagonal. (0.5+0.5).

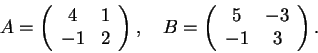
Resposta: Para calcular os autovalores calcularemos primeiro os polinômios característicos:

$$\vert A-\lambda I\vert= \left\vert \begin{array}{cc} 4-\lamb... ...nd{array}\right\vert = \lambda^2- 6 \lambda +9 =(\lambda^2-3).$$

Logo $\lambda=3$ é um autovalor duplo.

$$\vert B-\lambda I\vert= \left\vert \begin{array}{cc} 5-\lamb... ...right\vert = \lambda^2- 8 \lambda +12 =(\lambda-2)(\lambda-6).$$

Logo $\lambda=2$ e $\lambda=6$ são autovalores simples.

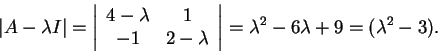
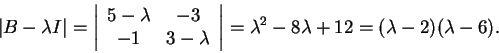
Para calcular os autovetores de 3, 2 e 6 devemos calcular, respectivamente,

$$(A-3I)X=0, \quad (B-2I)X=0, \quad (B-6I)X=0.$$

No primeiro caso obtemos o sistema:

$$x+y=0, \quad -x-y=0.$$

Ou seja, x=-y. Os autovetores são da forma (t,-t), $t\in \mathbb{R}$ e $t\ne 0$.

No segundo caso obtemos o sistema:

$$3x-3y=0, \quad -x+y=0.$$

Ou seja, x=y. Os autovetores são da forma (t,t), $t\in \mathbb{R}$ e $t\ne 0$.

No último caso obtemos o sistema:

$$-x-3y=0, \quad -x-3y=0.$$

Ou seja, x=-3y. Os autovetores são da forma (-3t,t), $t\in \mathbb{R}$ e $t\ne 0$.

A matriz A não é diagonalizável, pois não é possível encontrar uma base de autovetores (no máximo é possível encontrar um autovetor l.i.).

A matriz B é diagonalizável, pois existe uma base de autovetores: $\{(1,1), (-3,1)\}$.

Usando a base de autovetores $\{(1,1), (-3,1)\}$ de B temos,

$$\left( \begin{array}{cc} 4 & 1 \\ -1 & 2 \end{array}\rig... ...in{array}{cc} -1/4 & 1/4 \\ 1/4 & 3/4 \end{array}\right).$$

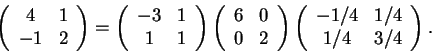
2) Considere a matriz

$$F = \left( \begin{array}{lll} 1 & 0 & 1 \\ 0 & 5 & 0 \\ 1 & 0 & 1 \end{array}\right)$$

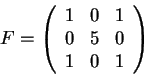
2.a) Encontre todos os autovalores de F e todos os autovetores de F. (0.5+0.5).

2.b) Encontre uma matriz R inversível, sua inversa R^-1 e uma matriz D diagonal tais que F = RDR^-1. ( 0.5+0.5+0.5).

Resposta: O polinômio característico de F é

$$\left\vert \begin{array}{ccc} 1-\lambda & 0 & 1 \\ 0 & 5-\... ...(1-\lambda^2) - (5-\lambda)= \lambda (5-\lambda) (2-\lambda).$$

Logo os autovalores são 5, 2 e 0 todos simples. (Observe que a soma dos autovalore é 7, igual ao traço da matriz, como deve ser).

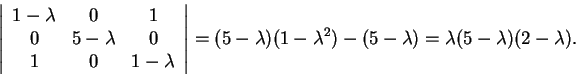
Os autovetores correspondentes são obtidos resolvendo os sistemas:

$$(F-5 I)(X)=0, \quad (F-2 I)(X)=0,\quad F(X)=0.$$

Obtemos os sistemas

$$-4x +z=0,\quad x-4z=0,$$

com solução (0,t,0). Logo os autovetores são da forma (0,t,0), $t\in \mathbb{R}$ e $t\ne 0$.

O segundo sistema é,

$$-x +z=0,\quad 3y=0, \quad x-z=0,$$

com solução (t,0,t). Logo os autovetores são da forma (t,0,t), $t\in \mathbb{R}$ e $t\ne 0$.

O último sistema é,

$$x +z=0,\quad 5y=0, \quad x+z=0,$$

com solução (t,0,-t). Logo os autovetores são da forma (t,0,-t), $t\in \mathbb{R}$ e $t\ne 0$. (Observe que os autovetores são ortogonais, como é de esperar numa matriz simétrica).

Temos, normalizando a base, o seguinte

$$\left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 5 & 0 \\ 1 & ... ... & 1 & 0 \\ 1/\sqrt{2} & 0 & 1/\sqrt{2} \end{array}\right),$$

onde a inversa de R é sua trasposta, pois é uma matriz ortogonal.

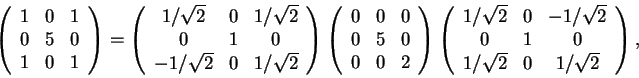
3) Considere a projeção ortogonal P no plano 2x+2y+z=0.

Escreva a matriz de P da forma B D B^-1, onde D é uma matriz diagonal. Ache B, D e B^-1 explicitamente. (B=1.0, D=1 e B^-1=0.5).

Resposta: O vetor normal ao plano de projeção (2,2,1), que é um autovetor de autovalor 0. Consideraremos agora dois vetores do plano ortogonais. Obteremos assim dois autovetores l.i. de autovalor 1. Tomando (1,-1,0) e $(1,-1,0)\times (2,2,1)= (-1,-1,4)$obtemos estes vetores. Temos que

$$\beta= \{(2/3, 2/3,1/3), (1/\sqrt{2}, -1/\sqrt{2},0), (1/\sqrt{18},1/\sqrt{18},-4/\sqrt{18}\}$$

é uma base de autovetores.

A expressão de P na base $\beta$ é

$$\left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right).$$

Portanto

$$P= \left( \begin{array}{ccc} 2/3 & 1/\sqrt{2} & 1/\sqrt{18} ... ... 1/\sqrt{18} & 1/\sqrt{18} & -4/\sqrt{18} \end{array}\right),$$

onde B^-1=B^t pois B é ortogonal.

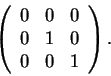
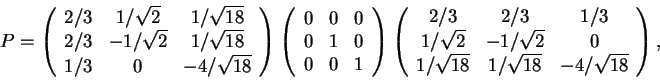
4) Para cada uma das matrizes abaixo, verifique se é uma rotação ou uma projeção ortogonal, ou nem uma coisa nem outra. Para a rotação identifique o eixo, e para a projeção o plano ou a reta onde é feita a projeção.

$$A = \left( \begin{array}{ccc} 1 & 6 & 1 \\ 6 & 5 & 7 \\ ... ... \\ 1/3 & 1/3 & 1/3 \\ 1/3 & 1/3 & 1/3 \end{array}\right),$$

$$C = \left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 1 & 1 \\ ... ...& \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array}\right).$$

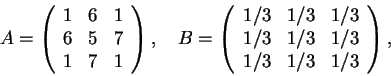
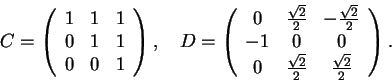
(Cada identificação 0.5, o plano ou reta de projeção 0.5, e o eixo de rotação 0.5).

Resposta: Observamos que uma projeção ortogonal é uma matriz simétrica e uma rotação é ortogonal.

Como a matriz A não é ortogonal não pode ser uma rotação. Como uma projeção tem traço 1 e a matriz A tem traço 7não é projeção. O de outra forma. Uma projeção tem determinante 0, como a matriz A tem determinante -1, não é projeção. Ou de outra forma. Uma projeção P verifica P²=P, e $A^2\ne A$.

Como a matriz C não é ortogonal não pode ser uma rotação. Como a matriz C não é simétrica não pode ser uma projeção.

A matriz B é simétrica e não é ortogonal. Logo a única possibilidade é que seja uma projeção. A matriz B tem todas as linhas iguais. Logo seu determinante é zero. Portanto, 0 é um autovalor. Os autovetores de 0 estão no plano x+y+z=0 (resolva o sistema correspondente). Logo 0 é um autovetor duplo (no mínimo é duplo, e como não pode ter multiplicidade 3, pois então a matriz seria nula ou teria traço zero, como preferir). O outro autovetor verifica $0+\lambda =1/3+1/3+1/3=1$ (o traço da matriz). Logo B tem autovalor 0 duplo e 1 simples. Logo, como é simétrica, é uma projeção na reta de vetor diretor o autovalor correspondente. Este autovetor é (1,1,1) (resolva o sistema ou veja que o vetor (1,1,1) pertence a reta de projeção).

A matriz D é ortogonal e não é simétrica. Logo a única possibilidade é que seja uma projeção. Como é ortogonal e estamos em dimensão três tem um autovalor $\pm 1$.

Se D fosse uma rotação 1seria um autovalor. Se um fosse autovalor o sistema a seguir teria solução não trivial (resolvendo este sistema também obteremos o eixo de rotação):

$$-x +\sqrt{2}/2 y -\sqrt{2}/2 z=0, \quad -x-y=0, \quad \sqrt{2}/2 y +(\sqrt{2}/2-1)z=0.$$

Temos x=-y. Substituindo

$$(\sqrt{2}/2+1)y +\sqrt{2}/2 z=0, \quad \sqrt{2}/2 +y(\sqrt{2}/2-1)z=0.$$

Temos $y+(1-\sqrt{2})z=$. Logo um autovetor é $(1-\sqrt{2}, \sqrt{2}-1,1)$.

Observe que, como a matriz é ortogonal, o plano de vetor normal $(1-\sqrt{2}, \sqrt{2}-1,1)$ é transformado nele próprio. Temos as seguintes possibilidades: ou a restrição de D a este plano é uma rotação ou não. No último caso haveria algum autovetor. Como D é ortogonal e estamos em um plano o vetor perpendicular também seria um autovetor. Logo D teria uma base ortogonal de autovetores, e em tal caso, seria simétrica. Como isto não ocorre, temos que D é uma rotação.

Dos raciocínios anteriores obtemos que se trata de uma rotação de eixo a reta $((1-\sqrt{2})t, (\sqrt{2}-1)t,t)$, $t\in \mathbb{R}$.