P1 de Álgebra Linear I - 2001.1

Data: 9 de abril de 2001.

Gabarito

1) Consider as retas

$$r_1=\{(1,1,1) +t(4,0,-2), \quad t\in \mathbb{R}\}, \qquad r_2=\{(1-2t,1,t), \quad t\in \mathbb{R}\}.$$

a) Estude a posição relativa das retas r₁ e r₂, isto é, descubra se são paralelas, reversas ou concorrentes. (0.5 pts)

b) Calcule a distância entre as retas r₁ e r₂. (1.0 pts)

c) Encontre um ponto P de r₁ tal que a distância de P a r₂ seja igual a distância entre r₁ e r₂. (0.5 pts)

d) Determine a área paralelogramo com vértices (1,1,1), (5,1,-1) (pontos de r₁) e $(1,1,0)\in r_2$(não é dado o quarto vértice). (1.0 pts)

e) Determine o paralelogramo com vertices (1,1,1), (5,1,-1) (pontos de r₁), $(1,1,0)\in r_2$e o quarto vértice em r₂. (0.5 pts)

f) Considere o plano $\pi$ que contém as duas retas r₁ e r₂. Determine dois vetores paralelos ao plano $\pi$ que não sejam colineares. (0.5 pts)

g) Determine o vetor normal do plano $\pi$. (0.5 pts)

h) Determine as equações cartesianas e paramétricas do plano $\pi$. (0.5 + 0.5 pts)

Resposta:

(a) Os vetores diretores da retas são colineares (4,0,-2)=-2(-2,0,1). Portanto, as retas ou são iguais ou são paralelas (diferentes). Para decidir é suficiente ver se o ponto $(1,1,1)\in r_1$ está em r₂, isto é, se é possível achar t tal que

$$1=1-2t, \quad 1=1+0t, \quad 1=0+t.$$

Da primeira equação temos t=0, que na terceira dá 1=0. Logo as retas são paralelas e diferentes.

(b) Como as retas são paralelas a distância d de r₁ a r₂ é a distância de qualquer ponto de r₂ a r₁. Escolhemos os pontos $A=(1,1,0)\in r_2$ e $B= (1,1,1)\in r_1$. Se N é o ponto de r₁ mais próximo de A teremos $d=\vert\overline{AN}\vert$ e

$$\overline{AB}= \overline{AN}+\overline{NB},$$

onde

$$\overline{NB}= (\overline{AB}\cdot v) v,$$

onde v é um vetor diretor unitário de r₁. Temos que $v=1/\sqrt{5}(-2,0,1)$ e que $\overline{AB}=(0,0,1)$, logo

$$\overline{NB}= ((0,0,1)\cdot (1/\sqrt{5}(-2,0,1))) 1/\sqrt{5}(-2,0,1)=(-2/5,0,1/5).$$

Logo

$$\overline{AN}=\overline{AB}- \overline{NB}= (0,0,1)-(-2/5,0,1/5)=(2/5,0,4/5).$$

E a distância é $\sqrt{2^2+4^2}/5= \sqrt{20}/5=\sqrt{4 \cdot 5}/{5}=2/\sqrt{5}$.

Observe que v. pode verificar que seus cálculos estão certos: o vetor $\overline{AN}$ deve ser perpendicular ao vetor diretor das retas (como pode ser verificado calculando o produto escalar, que é zero).

(c) Como as retas são paralelas vale qualquer ponto de r₁(veja o comentário no início da resposta do item (b).

(d) Sejam B=(1,1,1), C=(5,1,-1) (pontos de r₁) e $A=(1,1,0)\in r_2$. A área do paralelogramo procurado é o módulo do produto vetorial

$$\overline{BC}\times \overline{BA}= (4,0,-2)\times (0,0,-1)= (0,4,0).$$

Logo a área é quatro.

Observe que v. pode verificar este resultado. A área será $\vert\overline{BC}\vert \, d$ (d é a distância no item anterior), pois a distância entre as retas é a altura do paralelogramo. Como $\vert\overline{BC}\vert=\sqrt{20}$ e $d=2/\sqrt{5}$ temos

$$\sqrt{20}\, (2/\sqrt{5})= (\sqrt{4\cdot 5})( 2/\sqrt{5})=4.$$

Ou seja os cálculos sã coerentes.

(e) Observe que se D é o novo vértice temos

$$\overline{BD} =\overline{BA}+ \overline{AD}= \overline{BA}+ \overline{BC}=(0,0,-1)+ (4,0,-2)=(4,0,-3)$$

e que

D=B+(4,0,-3)=(1,1,1)+(4,0,-3)=(5,1,-2).

(verifique que este ponto está em r₂!)

(f) Um é o vetor diretor das retas, u=(2,0,-1) e outro (por exemplo) o vetor $v=\overline{AB}=(0,0,1)$.

(g) O vetor normal ao plano é

$$u\times v=(2,0,-1)\times (0,0,1)=(0,-2,0).$$

Logo podemos escolher n=(0,1,0) como vetor normal ao plano.

(h) A equação cartesiana é 0x+1y+0z=d onde d é obtido pela condição $A\in \pi$, ou seja y=1.

As equações paramétricas são (usando os vetores do item (f)) e o ponto A=(1,1,0),

$$\{x=1+2t+0s \quad y=1+0t+0s, \quad z=0-t+s, \quad t,s\in \mathbb{R}\}.$$

Por exemplo, observando que (1,0,0) e (0,0,1) também são vetores paralelos ao plano (pois são ortogonais ao seu vetor normal (0,1,0)) e considerando o ponto (0,1,0) do plano temos outras

$$\{x=t \quad y=1 \quad z=s, \quad t,s\in \mathbb{R}\}.$$

2) Considere a reta r dada pelas equações

$$x+y+z=1, \quad x-y-z=1$$

e o ponto P=(1,0,1).

a) Determine o vetor diretor de r. (0.5 pts)

b) Determine as equações paramétricas de r. (0.5 pts)

c) Encontre um ponto A de r tal que o vetor $\overline{AP}$ seja ortogonal ao vetor diretor de r. (1.0 pts)

d Calcule a distância de P à reta r. (0.5 pts)

Resposta:

(a) O vetor diretor v de r é obtido como o produto vetorial dos vetores normais dos planos. Ou seja,

$$v=(1,1,1)\times (1,-1,-1)= (0,2,-2),$$

isto é, podemos tomar v=(0,1,-1).

Outra forma seria resolver o sistema, restando a segunda da primeira equação temos

$$2y +2z=0,\quad y=-z.$$

Na primeira equação temos x=1-y-z=1-y+y=1. Logo, escolhendo y como parámentro, a equação da reta é

$$x=1, \quad y=t, \quad z=-t, \quad t\in \mathbb{R} .$$

E o vetor diretor é (0,1,-1). Observe que com este método resolvemos também o item (b).

(b) Se v. não resolveu o item (a) pelo segundo método é suficiente procurar um ponto do plano (por exemplo (1,0,0)) e escrever

$$x=1+0t \quad y=0+t, \quad z=0-t, \quad t\in \mathbb{R} .$$

(c) Considere um ponto da reta, por exemplo Q=(1,0,0), e observe que

$$\overline{QP}=\overline{QA}+\overline{AP}, \quad \overline{QA... ...c{v}{\vert\vert v\vert\vert}) \frac{v}{\vert\vert v\vert\vert}$$

onde v=(0,1,-1) é o vetor diretor da reta. Se A=(x,y,z) temos

$$\begin{array}{ll} (0,0,1)&= ((0,0,1)\cdot (0,1/\sqrt{2}, -1/\... ...-x,-y,1-z)=\\ &=(0,-1/{2}, +1/{2}) + (1-x,-y,1-z). \end{array}$$

Portanto,

A=(x,y,z)=(0,-1/2, +1/2)- (0,0,1)+(1,0,1)=(1,-1/2,1/2).

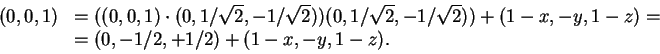
(d) O módulo do vetor $\overline{AP}=(0,1/2,1/2)$ é a distância procurada, $\sqrt{2}/2$.

Observe que há um modo de verificar que o resultado é coerente, o vetor $\overline{AP}$ é ortogonal ao vetor diretor da reta (faça o produto escalar e veja que é zero).

3) Considere os planos definidos abaixo:

$$\Pi = \{ (x,y,z) \ \vert \ 2x + y -z = 1 \}, \quad \Pi '= \{ (x,y,z) \ \vert \ x + 3y -z = -1 \}$$

a) Encontre um terceiro plano $\Pi''$ tal que a interseção dos três planos $\Pi,$ $\Pi'$ e $\Pi''$ seja um único ponto. (1.0 pts)

b) Encontre um terceiro plano $\Pi''$ (diferente de $\Pi$ e $\Pi^\prime$) tal que a interseção dos três planos $\Pi,$ $\Pi'$ e $\Pi''$ planos seja uma reta. (1.0 pts)

Resposta: Para o item (a) é suficiente considerar um plano cujo vetor normal não esteja no plano (vetorial) gerado pelos vetores normais dos planos $\Pi$ e $\Pi^\prime$. Por exemplo $\Pi^{''}\colon x=0$.

Outra possibilidade é procurar um plano cujo vetor normal seja a reta de interseção de $\Pi$ e $\Pi^\prime$. Este vetor normal é $(2,1,-1)\times (1,3,-1)=(2,1,5)$. Logo o plano procurado é (por exemplo) 2x+y+5z=0. Deixamos para v. verificar que os três planos se intersetam em um ponto. (resolva o sistema!)

Para o item (b) fazemos o seguinte. Observe que $\Pi\cap \Pi^\prime$é uma reta r (pois os planos não são paralelos). Se $\Pi\cap \Pi^\prime\cap \Pi^{''}$ é uma reta essa reta é necessariamente r!. Portanto, $r\subset \Pi^{''}$. Então podemos escolher como $\Pi^{''}$ qualquer plano que contenha r e seja diferente dos outros dois planos.

Determinemos r. Seu vetor diretor já foi obtido como o produto vetorial dos vetores normais dos planos $\Pi$ e $\Pi^\prime$, (2,1,5). Um ponto de r é (0,-1,-2). Logo $r\colon (2t, -1+t, -2+5t)$, $t\in \mathbb{R}$.

Para determinar $\Pi^{''}$ devemos encontrar um ponto que não pertença aos outros planos. Por exemplo, P=(1,0,0). Então é suficiente considerar $\Pi^{''}$ como o plano que contém a r e a P. O vetor nomal n do plano é perpendicular aos vetores diretores (2,1,5) e (1,1,2) do plano. Logo $n=(2,1,5)\times(1,1,2)=(-3,1,1)$. Logo $\Pi^{''} \colon 3x -y -z=d$ onde d é obtido por $(1,0,0)\in \Pi^{''}$, d=3.

Outra solução é procurar planos da forma

$$\lambda (2x+y-z) +\mu (x+3y-z)= \lambda -\mu,$$

para $\lambda$ e $\mu$ não nulos (tomando $\lambda=2$ e $\mu=-1$obtemos o plano anterior).