P3 de Álgebra Linear I - 2001.1

Data: 20 de junho de 2001.

to to 0.7Nome:  Matrícula: to to 0.7Assinatura: Turma:

Questão	Valor	Nota	Revisão
1	2.5
2	2.5
3	2.5
4	3.0
Total	10.0

Instruções:

• Não é permitido usar calculadora. Mantenha o celular desligado.
• Justifique todas as respostas. Escreva de forma clara, legível e organizada.
• Em cada uma das questões da prova não haverá pontuação parcial - Verifique cuidadosamente suas respostas.
• Faça a prova na sua turma.

1) Considere as matrizes

$$A= \left( \begin{array}{cc} 4 & 1 \\ -1 & 2 \end{array}\... ...t( \begin{array}{cc} 5 & -3 \\ -1 & 3 \end{array}\right).$$

a) Determine os autovalores e autovetores das matrizes A e B. (0.5+0.5).

b) Estude se estas matrizes são diagonalizáveis. (0.5).

c) Escreva as matrizes diagonalizáveis do item anterior na forma R D R^-1 onde D é uma matriz diagonal. (0.5+0.5).

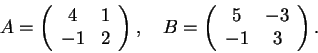
2) Considere a matriz

$$F = \left( \begin{array}{lll} 1 & 0 & 1 \\ 0 & 5 & 0 \\ 1 & 0 & 1 \end{array}\right)$$

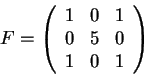
2.a) Encontre todos os autovalores de F e todos os autovetores de F. (0.5+0.5).

2.b) Encontre uma matriz R inversível, sua inversa R^-1 e uma matriz D diagonal tais que F = RDR^-1. ( 0.5+0.5+0.5).

3) Considere a projeção ortogonal P no plano 2x+2y+z=0.

Escreva a matriz de P da forma B D B^-1, onde D é uma matriz diagonal. Ache B, D e B^-1 explicitamente. (B=1.0, D=1 e B^-1=0.5).

4) Para cada uma das matrizes abaixo, verifique se é uma rotação ou uma projeção ortogonal, ou nem uma coisa nem outra. Para a rotação identifique o eixo, e para a projeção o plano ou a reta onde é feita a projeção.

$$A = \left( \begin{array}{ccc} 1 & 6 & 1 \\ 6 & 5 & 7 \\ ... ... \\ 1/3 & 1/3 & 1/3 \\ 1/3 & 1/3 & 1/3 \end{array}\right),$$

$$C = \left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 1 & 1 \\ ... ...& \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array}\right).$$

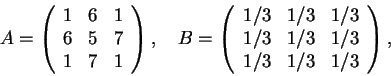
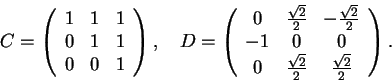
(Cada identificação 0.5, o plano de projeção 0.5, e o eixo de rotação 0.5).